BuddhiLW/julia-simulations

Simulating random walks, Kelly Criterion, and Thorpe's calculations on blackjack; Using also some Monte Carlo

Notes

(setq org-format-latex-options (plist-put org-format-latex-options :scale 3.0))


* Kelly Criterion
** Bias coin-toss
Let $X_i$ be the bankroll, in the moment of the =i-th= coin-toss.

\begin{equation}
\begin{aligned}
X_{n}&=X_{n-1}+\,T_{k}\,B_{k} \\
\Leftrightarrow X_{n}&=X_{0}+\sum_{k=1}^{n}\,T_{k}\,B_{k}
\end{aligned}
\end{equation}

The expectation is:
$E(X_{n})=X_{0}+\sum_{k=1}^{n}E(B_{k}T_{k})=X_{0}+\sum_{k=1}^{n}(p-q)E(B_{k})$

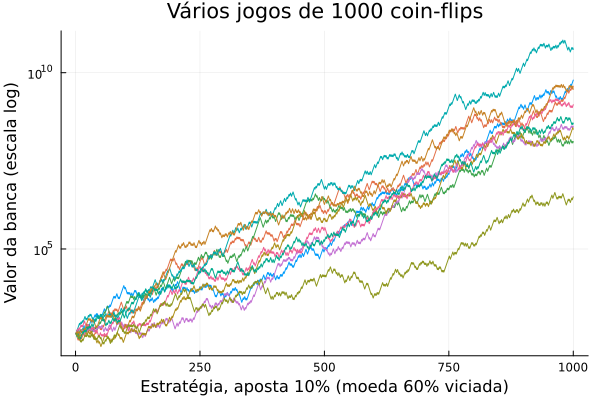
Following this formula, we can simulate these =Random Walks= and even measure, through Monte Carlo Method, the =Probability of Ruin=, given $(p,B_k)$, in which =T= is the outcome - either 1 or -1 (win or lose).

** Using Julia to Simulate the =Random Walk=
using Random, Distributions, Plots

moeda_viciada = Binomial(1, 6/10)
p = plot()
for m=1:10
    v0=400
    n=1000
    jogadas = rand(moeda_viciada, n)
    v=zeros(n)
    v[1]=v0
    for i=1:n-1
        if jogadas[i] == 1
            v[i+1] = v[i] + 1*(0.1*v[i])
        else
            v[i+1] = v[i] - 1*(0.1*v[i])
        end
    end
    plot!(v[1:n], yaxis=:log)
end

for m=1:10
    v0=400
    n=1000
    jogadas = rand(moeda_viciada, n)
    v=zeros(n)
    v[1]=v0
    for i=1:n-1
        if jogadas[i] == 1
            v[i+1] = v[i] + 1*(0.2*v[i])
        else
            v[i+1] = v[i] - 1*(0.2*v[i])
        end
    end
    plot!(v[1:n], yaxis=:log)
end

plot(p, title="Vários jogos de 1000 coin-flips", xlabel="Estratégia, aposta 10% vs 20% (moeda 60% viciada)", ylabel="Valor da banca (escala log)", legend=false)

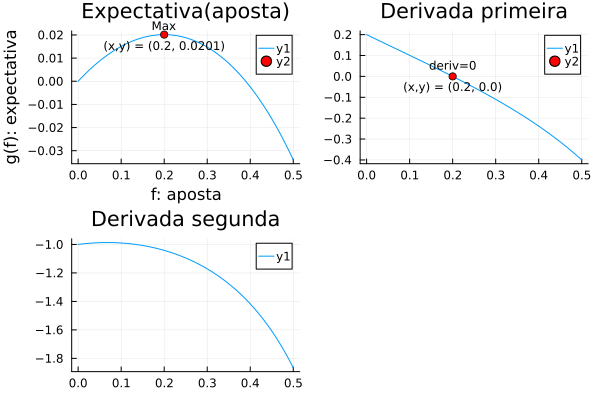
savefig("estrategia-moeda-viciada.png")

Using Julia to Simulate the expected-value of the growth rate coefficient

function g(p,q,f)
    return p*log(1+f) + q*log(1-f)
end

fs = range(0,0.5, 100)

function gl(p, q, f)
    return (p-q-f)/((1-f)*(1+f))
end


function gll(p,q,f)
    return (-p/(1+f)^2) + (-q/(1-f)^2)
end

p1=plot(fs,g.(0.6, 0.4,fs), title="Expectativa(aposta)", xlabel="f: aposta", ylabel="g(f): expectativa")
scatter!([0.2],[g(0.6,0.4,0.2)], mc=:red)
annotate!(0.2, 0.021, text("Max", :bottom, 8))
annotate!(0.2, 0.018, text("(x,y) = (0.2, 0.0201)", :top, 8))
p2=plot(fs, gl.(0.6,0.4,fs), title="Derivada primeira")
scatter!([0.2], [0], mc=:red)
annotate!(0.2, 0.02, text("deriv=0", :bottom, 8))
annotate!(0.2, -0.02, text("(x,y) = (0.2, 0.0)", :top, 8))
p3=plot(fs, gll.(0.6,0.4,fs), title="Derivada segunda")
plot(p1,p2,p3)
savefig("expectativa.png")
plot(p2)

Using Julia to Simulate Probability of Ruin

Monte Carlo

TODO: Comments about integrals with Monte Carlo and the method itself.

Exercises

Book: Y. A. Rozanov, Probability Theory - A concise course

Julia functions for solving the execies

Binomial, or Combination of x, by y

function C(x,y)
    return factorial(x)/(factorial(y)*factorial(x-y))
end

1.1

A four-volume work is placed in random order on a bookshelf. What is the probability of the volumes being in proper order from left to right or from right to left?

Answer

The $(b_1, b_2, b_3, b_4)$, 4-tuple is the space we are dealing in.

There are $N=4!$ combinations possible for this space. And, only two that benefits us, that is, in order of volumes from right to left, and left to right.

Therefore, the probability of these events happening randomly is:

\begin{equation} \begin{aligned} P(A) &= \dfrac{N(A)}{N}
⇔ P(A) &= \dfrac{2}{4!} \ ⇔ P(A) &= \dfrac{1}{12} \ \therefore P(A) &= 0.0833 \end{aligned} \end{equation}

import Pkg; Pkg.add("CSV")
import Pkg; Pkg.add("DataFrames")
1/12

A wooden cube with painted faces is sawed up into 1000 little cubes, all of the same size. The little cubes are then mixed up, and one is chosen at random What is the probability of its having just 2 painted faces?

Ans: 0.096

Answer

The space of colored sawed-cubes come all from the border of the former wooden cube (supposedly). The inner sawed-cubes parts aren’t painted.

Then, the cubes that only have two colors, must come from the edges of the cube, but not from it’s vertices - which would have three color-faces.

There are 12 edges; there are 8 vertices; each edge has 10 cubes, of which 8 aren’t vertices - because there are 1000 sawed-cubes, of same volume ($\text{cubes} = 10*10*10$) and the two vertices in an edge are a cube of three colored face.

Thus, the edge cubes that aren’t vertices are: $(12 * 8)$.

The total cubes are 1000.

$\therefore P(A) = 96/1000 \quad ↔ \quad P(A) = 0.096$

1.3

A batch of n manufactured items contains k defective items. Suppose m items are selected at random from the batch. What is the probability that l of these items are defective?

Answer

• n: manufactured.
• k: defected out of the n defected.
• m: selection-size.
• l: number of selected items, out of the m selected, which are defected.

By theorem 1.3, given here, without proof (see the book for proof),

THEOREM 1.3. A population of n elements has precisely \begin{equation} \begin{aligned} C_r^n = \dfrac{n!}{r!(n-r)!} \end{aligned} \end{equation} subpopulations of size r < n.

So, your total number of combinations m-selections is exactly the binomial coeficient $N=C_mⁿ$, or $\genfrac{(}{)}{0pt}{}{n}{k}$.

The total of combination of m-selections, in which l are defected, follows from:

• l of those m-selected are defected.
• There are k defected in the population.
• $l-m$ of the selected are not defected, and they come from the $n-m$ population of non-defected.

Thus, the number of possible combinations of selecting l from m, which are defected can be numbered by: multiplying the combination l-selected from k population, and the combination of (l-m)-selected from the (n-m) population.

$\therefore N(A)=C_l^k * C_l-m^n-m$

Finally, the probability of this event happening is: $P(A)=\dfrac{N(A)}{N} \, ⇔ \, P(A)=\dfrac{C_l^k * C_l-m^n-m}{C_m^n}$

1.4

Ten books are placed in random order on a bookshelf. Find the probability of three given books being side by side.

Ans: \dfrac{1}{15}

Answer

Theorem of possible placements of books in a shelf (BLW:1.1)

Proof by Induction.

If we think of, for example, 4 books in total, and we take the first 3 to be our side-by-side group. They could be the first three, or the last three. That is, (4-3)+1 possible placements.

If that’s true for n-1 books, and m that we want side-by-side, that is: ((n-1)-m)+1. e.i., n-m placements, side-by-side, not-regarded of order. Then, if we have n+1 books.

Let’s say the n-ith book in the shelf is not one of our m books (and, implicitly assumed, is in the end of the shelf).

Then, we will have one more slot we can swap the m books further, with this new book. Furthermore, the previous (n-m) places are still there. Therefore, we will have (n-m)+1 placements. QED.

Answer per-se

All possible arrangements are given by the factorial: $N=10!$

There are 10-3+1, i.e., 8, places the three books can be put side by side, by <a href=”*Theorem of possible placements of books in a shelf (BLW:1.1)”>BLW:1.1.

For each 7 placements, there can be 3! possible displacements. Furthermore, for each of the possible combinations of side-by-side tree-books in a displacement, there are 7! combinations for the rest of the books. That is, $N(A)=8(3!)(7!)$, by T1.1, about the number of possible ordered-pairs.

\begin{equation} \begin{aligned} \therefore P(A) &= \dfrac{N(A)}{N} \, ⇔ \, P(A) = \dfrac{8(3!)(7!)}{10!}
\therefore P(A) &= \dfrac{1}{15} \end{aligned} \end{equation}

By Julia calculation:

8*(factorial(3)*factorial(7))/(factorial(10))

1/15

Another shorter solution

The number of possible subpopulations of the books is $C_3¹⁰$. Out of these, we want exactly one of them.

But, this subpopulation can be in (10-3)+1 possible displacements, by BLW:1.1.

$\therefore P(A) = \dfrac{8}{C_3¹⁰} \, ⇔ \, P(A) = \dfrac{8(3!)(7!)}{10!}$

Thus, $P(A)=0.06667$, or $P(A)= \dfrac{1}{15}$.

1.5

1. One marksman has an 80% probability of hitting a target, while another has only a

70% probability of hitting the target. What is the probability of the target being hit (at least once) if both marksman fire at it simultaneously?

Answer

The probability of the first marksman not hitting the target is 1 minus their probability of hitting the target, which is 1 - 0.8 = 0.2. Similarly, the probability of the second marksman not hitting the target is 1 - 0.7 = 0.3.

Since the marksmen are firing simultaneously, we can multiply the probabilities together to find the probability of both marksmen missing the target: 0.2 * 0.3 = 0.06.

Finally, we subtract this probability from 1 to find the probability of the target being hit at least once: 1 - 0.06 = 0.94.

Therefore, the probability of the target being hit (at least once) when both marksmen fire at it simultaneously is 0.94 or 94%.

Mathematically, the change of both not hitting: \begin{equation} \begin{aligned} P(A ∪ B) &= P(A) + P(B) - P(A ∩ B)
\implies P(A ∪ B) &= 0.8 + 0.7 - 0.8*0.7 \ \therefore P(A ∪ B) &= 0.94 \end{aligned} \end{equation}

Or, \begin{equation} \begin{aligned} 1-\overline{P(A ∪ B)} &= 1-(\overline{P(A)} ∩ \overline{P(B)})
\implies 1-\overline{P(A ∪ B)} &= 1 - (1-0.8) * (1-0.7) \ \therefore \implies 1-\overline{P(A ∪ B)} = 0.94 \end{aligned} \end{equation}

1.6

Suppose n people sit down at random and independently of each other in an auditorium containing n + k seats. What is the probability that m seats specified in advance (m < n) will be occupied?

Answer

ChatGPT (Wrong answer)

First, let’s consider the total number of possible seating arrangements. There are (n + k) seats available and n people to be seated. The number of ways to arrange n people in (n + k) seats is given by the binomial coefficient, denoted as C(n + k, n) or (n + k choose n). This can be calculated as:

C(n + k, n) = (n + k)! / (n! * k!)

Next, let’s consider the number of ways to choose m specified seats, which are the seats we want to be occupied. We can select m seats out of the available m + k seats in C(m + k, m) ways, which is given by:

C(m + k, m) = (m + k)! / (m! * k!)

Finally, to find the probability that exactly m specified seats are occupied, we divide the number of ways to have m occupied seats by the total number of possible seating arrangements:

P(m seats occupied) = C(m + k, m) / C(n + k, n)

Therefore, the probability that m specified seats will be occupied is C(m + k, m) / C(n + k, n).

ChatGPT confuses itself in the following reasoning:

Next, let’s consider the number of ways to choose m specified seats, which are the seats we want to be occupied. We can select m seats out of the available m + k seats in C(m + k, m) ways (…).

Own answer

There are C(n+k,n) possible groups of sittings used by n people, in n+k sits.

We pre-arrange certain seats of m-size out of n+k available sits, in total a of C(n+k, m) arrangements.

But, only one m-sized grouping is of interest, namely the one in which all the m pre-assigned sits are sit by a subgroup of n people. Furthermore, there are $\dfrac{n!}{m!}$ arrangements possible, for this m-sized group of sits of interest, which will be of no concern. Because, the possible ways to chose C(n+k,n) doesn’t consider order.

Still, we can still have C(n-m+k, n-m) possible grouping-of-fills of left-over placements.

Thus, $N(A)=1*C(n-m+k, n-m)$ are the number of events of interest. I.e., n-grouped sittings of which m are pre-assigned out of n+k sits. And n-m left open to possible groupings, in n-m+k sits.

And, $N=C(n+k,n)$ are the total arrangements of n-grouped sits.

\begin{equation} \begin{aligned} \therefore P=\dfrac{C(n-m+k,\, n-m)}{C(n+k,n)} \end{aligned} \end{equation}

function C(x,y)
    return factorial(big(x))/(factorial(big(y))*factorial(big(x-y)))
end
function P(n,m,k)
    return C(n-m+k, n-m)/C(n+k,n)
end

P(109,55,1)

Notes

if n+k, k=1 and $m=\frac{n+1}{2}$, $∀(n,m)$. Then, $P(A) = \dfrac{1}{2}$

\begin{equation} \begin{aligned} C(n-m+k,\, n-m) = \dfrac{(n-m+k)!}{[(n-m+k)-(n-m)]!(n-m)!} \end{aligned} \end{equation}

\begin{equation} \begin{aligned} P &= \dfrac{(n-m+k)! × n!k!}{[(n-m+k)-(n-m)]!(n-m)! × (n+k)!}
⇔ P &= \dfrac{(n-m+k)! × n!k!}{k!(n-m)! × (n+k)!} \end{aligned} \end{equation}

Substituting m, \begin{equation} \begin{aligned} P = \dfrac{(\frac{n+2k-1}{2})! × n!k!}{(k! (\frac{n-1}{2}))! × (n+k)!} \end{aligned} \end{equation}

Substituting k=1 \begin{equation} \begin{aligned} P &= \dfrac{(\frac{n+1}{2})! × n!}{(\frac{n-1}{2})! × (n+1)!}
\implies P &= \dfrac{(\frac{n+1}{2})!}{(\frac{n-1}{2})! × (n+1)} \ \implies P &= \dfrac{(\frac{n+1}{2})(\frac{n-1}{2})!}{(\frac{n-1}{2})! × (n+1)}\ \implies P &= \dfrac{(\frac{n+1}{2})}{(n+1)} \ \implies P &= \dfrac{(n+1)}{2×(n+1)} \ \therefore P &= \dfrac{1}{2} \quad, ∀(n,m) \end{aligned} \end{equation}

1.7

Three cards are drawn at random from a full deck. What is the probability of getting a three, a seven and an ace?

Answer

In a deck, there are 4 threes, sevens and aces. And a total of 52 cards. $4^3$ groupings constituting one of these three cards. And, a total of C(52,3) possible groupings.

\begin{equation} \begin{aligned} P(A) &= \dfrac{N(A)}{N}
\implies P(A) &= \dfrac{4^3}{C(52,\, 3)} \ \implies P(A) &= \dfrac{3!(4^3)}{52!51!50!} \end{aligned} \end{equation}

function C(x,y)
    return factorial(big(x))/(factorial(big(y))*factorial(big(x-y)))
end

(factorial(3)*4^3)/(52*51*50)

$\therefore\, P(A)=0.290\%$

Notes 1

The total combination, with order, of possible three cards being draw is:

52*51*50

If we consider 12 cards - any of the threes, sevens and aces. Then, either two of them. Finally, the final one, of the three kinds of cards. There are in total, 384 possible arrangements of these draws.

12*8*4

The same can be accounted, if we think of the possible groupings of the three kinds, of which exist four elements of each type - in total: $4^3$.

Finally, there are $3!$ possible arrangements - with order - of these groupins.

Again, we get 384 possible arrangements of these draws.

factorial(3)*4^3

We also can think of only possible groupins $4^3$ which expresses our objective-event. Thinking in the same domain, of groupins - without order - we have $C(52,3)$ possible kinds of groupings of three cards, out of 52 cards of a deck.

This gives us the same probabily-value: $\dfrac{4^3}{C(52,3)}=\dfrac{3!(4^3)}{52*51*50}$

Notes 2

((factorial(3)*4^3)/(52*51*50)) / (1/(12*11*10))

((factorial(4)*4^4)/(52*51*50*49)) / (1/(16*16*15*14))

1.8

What is the probability of being able to form a triangle from three segments chosen at random from five line segments of lengths 1, 3, 5, 7 and 9?

Answer