Welcome to my CS50 final project.

Updates

17/02/2023 - Addition of Optimistic Initialization Algorithm.
16/02/2023 - Addition of the Softmax Algorithm.
14/02/2023 - Correction of regret computation, cumulative regret is visually logarithmic on figures.
03/01/2023 - Addition of Epsilon Greedy Decay algorithm.
26/12/2022 - Completed CS50 Project.

A video description of my project, required to be below 3 minutes by CS50. For an in-depth explanation of the code, please continue and read the full document. Video Demonstration

Definitions.

Term	Notation	Description
Action	$A_t$	Action taken by the agent at time step $t$.
Observation	$O_t$	Observation received by the agent from the environment after taking and action.
Reward	$R_t$	Scalar feedback signal for an action.
State	$S_t$	The state of the environment or the internal state of the agent.
Return	$G_t$	Cumulative reward over time steps.

1.0 Introduction.

Here I will be exploring reinforcement learning (RL), a type of machine learning that aims to interact with an environment in order to improve. Unlike machine learning methods you are probably used to (do not worry if you are not) RL needs to interact with this environment in order to learn. A great example of RL comes from DeepMind where they produced an agent that learnt to play atari games to a human level and above! This project will not be tackling tasks at that level however, I will be exploring what is called "The multi-armed bandit problem". This is a much simpler version of the full RL problem and can be thought of like going to the casino and playing the slot machines. I will explain it in much more detail below, if you are familiar with the multi-armed bandit problem and the algorithms implemented feel free to just jump straight to the code.

Important Files.

main.py - Where the environment and agent class instances are created, alongside some function calls for plots.
bandit_env.py - The code for the multi-armed bandit environment.
bandit_algos.py - The code for each of the multi-armed bandit algorithms.
plotting.py - Code for all the plots you can make.

Once this project is complete, feel free to clone the repo and have a play around with the code, I will also include my references with links to their blogs/code at the bottom of this file.

2.0 Multi Armed Bandit Problem

You are at a casino, there are plenty of slot machines around you. these are the one armed bandits, (named according because slot machines used to have a big leaver to pull). Each of these bandits return to us some reward (this could be positive or negative), but we do not know what that reward is. What is the best strategy to obtain the most profit? Which bandits should we pull the most so we leave with the most money? Or do we just let luck do its thing and hope we leave with more money than we entered with?

This problem is also called the "explore or exploit" problem. The idea of when should we explore for more knowledge (try out that bandit we haven't pulled yet to see if it gives us more profit), or exploit the knowledge we have already (stick on the bandit we know is currently giving us the most profit). Researchers have been looking at this problem and have implemented some very cool algorithms to try and solve this problem! This project looks to implement and explore them.

2.1. The Environment.

We need the environment to do several things for this problem. 1st, we need to set the number of bandits we need, the mean return of each bandit and the probability of us getting that reward. For now I am going to implement a stationary bandit, where the reward remains the same throughout each game. However, later on, I will implement a bandit where the returns are dynamic, sampled from a reward distribution. This should make the problem slightly harder for the algorithms to learn from.

For this set up, we are going to create and environment class, where we can create instances of the environment and pass them in as parameters when we are creating our agents.

The environment must do certain things.

Take in an array or rewards and reward probabilites as arguments.
Given an action, return the reward to the agent.

To create the environment, I will be using OpenAI's Gym.

2.2. Agents

There are plenty of algorithms that have been created to solve bandit problems (Do not worry if you do not know how they work, I will to explain how each of them works). In this implementation of the problem, our agent will take in the environment as a parameter and conduct its actions. The actions the agent takes and rewards of its actions will be stored and our agent should present these results to a few plotting functions that will create some nice graphs for us.

The agents I plan to implement are:

Random Agent.
Greedy Agent.
$\epsilon$-greedy Agent.
$\epsilon$-Greedy Decay Agent (Added after submission to CS50).
Upper Confidence Bound (UCB) Agent.
Thompson Sampling Agent.
Softmax Agent (Added after submission to CS50).
Optimistic Initialization Agent (Added after submission to CS50).

2.2.1 The Random Agent.

This agent has no concept of what is going on, they simply just pull whatever bandit they want, regardless of reward, or how many times they have pulled it. This idea can be thought of as simply closing your eyes at the casino and pulling any of the slot machines you fancy.

2.2.2 The Greedy Agent.

Before discussing this agent, I first need to introduce a concept of evaluating our actions, this allows us to learn about what actions are better than others.

Let us define the Action Value.

$$ q(a) = \mathbb{E} \space [R_t \space | A_t = a] $$

The action value $q(a)$, is the reward we expect to receive given that we take action $a$. A simple way to learn and estimate the action value is to average out the rewards we have received taking that specific action. This can be computed such that:

$$Q_t(a) = \frac{\sum_{n = 1}^t I(A_n = a)R_n}{\sum_{n = 1}^t I(A_n = a)}$$

Our estimate of the action value at time step $t$ $(Q_t(a))$ is computed by summing the rewards we have received taking that action, over how many time we have taken that action. The indicator function $I(\cdot)$ = 1 if action $A_n = a$ and = 0 if $A_n \neq a$. This basically allows us to pick out the time steps where we actually took action $a$.

However, storing all of the rewards and computing this will be really inefficient when are selecting actions in a larger series. Instead we can incrementally update our estimate of the action value using the equation below:

$$ Q_t(A_t) = Q_{t-1}(A_t) + \alpha_t(R_t - Q_{t-1}(A_t))$$

Where $\alpha_t = \frac{1}{N_t(A_t)}$ where $N_t(A_t)$ is the count of the action $A_t$.

Now that we have covered the theory and maths of the action value and how we update it, lets talk about the Greedy Agent.

Unlike the random agent that selects its actions randomly, the greedy agent will pick the action that has the highest estimate. Its policy is defined as:

$$ \pi_t(a) = I(A_t = \underset{a}{\arg\max} Q_t(a)) $$

This means that the greedy agent will pick action $A_t$ with the highest action estimate $Q_t(a)$. Where $I(\cdot)$ is the indicator function that = 1 if the action is the highest action value and = 0 if not.

This of course has disadvantage of falling into suboptimal decisions.

Consider the following:

There are 4 bandits that the greedy algorithm can select, with values of [1, 2, 3, 4] respectively, they all pay out with a probability of 1. All action values are initialized to 0, meaning that the agent will select an action at random (this is called breaking ties randomly). If the agent picks bandit 4 randomly, then HAPPY DAYS! We update our action value for that action, giving it a value higher than 0, and the agent will continue to select that action for the rest of the game. However, if we picked action 1, 2, or 3 we would remain stuck in a suboptimal action for the rest of the game. This is not what we want.

If the bandits pay out with a certain probability, consider the bandits above, but they pay out with probability [0.3, 0.8, 0.4, 0.2], we get a similar situation. This time the agent will pull arms randomly until it finally gets a reward.

Of course this is not the best algorithm if we want to leave the casino with the most money. But if you run the greedy agent against the random agent a few times, if we are lucky, the agent will select the highest paying bandit, meaning it will outperform the random agent.

2.2.3 The $\epsilon$-Greedy Agent

Now that we have explored the greedy agent, we understand that an RL agent can compute an value of an action "$Q_t(a)$" that allows it to reason on what actions to choose. However, the greedy agent will commit to the first bandit that rewards it, which means it can find suboptimal solutions really easily. Researchers have come up with an algorithm, the "$\epsilon$-greedy algorithm" that allows the agent to exploit the knowledge it has gotten so far, but with a certain probability $(\epsilon)$ of exploring other actions. This allows the agent to continue to explore its other options, ensuring that the action the agent is taking is the optimal action.

The policy of an $\epsilon$-greedy algorithm is such:

$$ \pi_t(a) = \begin{bmatrix} (1-\epsilon) + \epsilon / |A| \space \space \text{if} \space \space Q_t(a) = \max_b Q_t(b) \end{bmatrix}$$

$$\begin{bmatrix} \epsilon/|A| \space \space \text{otherwise} \end{bmatrix}$$

Where $|A|$ denotes the number of choices that the agent can select. Note that the optimal action can still be selected when we are randomly choosing actions with probability $\epsilon$.

This is a very popular algorithm, although in this case its very simple, it has been used to great effect. The DeepMind Atari playing agent uses an $\epsilon$-greedy policy!!!!

2.2.4 The $\epsilon$-Greedy Decay Algorithm.

Exploring with probability $\epsilon$ is great as it allows our agent to continue to explore other actions in case there is a better option out there. However, the probability of exploration is set in stone during the whole experiment; meaning as the experiment draws to a close, we are still just a likely to try other options as we were at the start. Throughout working with this project, I have seen that the $\epsilon$-Greedy algorithm has accurate estimates of the Q value for each arm at the end of experiments that are just 1000 time steps in length. Yet we continue to explore other options at a set probability.

This is why I have implemented an $\epsilon$-Greedy Decay Agent, this works in the exact same manner as the $\epsilon$-Greedy Agent, but the value of $\epsilon$ is dynamic. Early in the experiments, the epsilon value is high (the default value = 1), however at each time step, we decay $\epsilon$. We do this by multiplying epsilon by a decay rate (default value = 0.99). This means as time steps increase, epsilon decreases. This will allow the agent to explore early on, while exploiting the knowledge it has gained as time steps increase.

2.2.5 Upper Confidence Bounds (UCB) Agent.

The UCB agent, is the first agent I am implementing that shows "optimism is the face of uncertainty". What does this mean? UCB allows us to quantify not just the action value estimate but how confident the agent is about that estimate. If we are more unsure about an action, lets be optimistic about its value.

Lets look at how the UCB takes actions.

$$ a_t = \underset{a \in A}{\arg\max} Q_t(a) + U_t(a) $$

Meaning that action $a_t$ is chosen such that it maximizes the action value estimate + $U_t(a)$.

$U_t(a)$ is the quantification of certainty of our estimate of the action value. This value is dependent on the count $N_t(a)$, meaning the higher the count of the action, the smaller the value of $U_t(a)$ as we should be confident about out action value estimate. The lower the count the higher the value of $U_t$. This means actions will be selected if we have not explored them enough, or if they have a large action value. This computation allows us to explore actions based on their potential to be the optimal action.

But how do we compute our confidence of our action estimate?

Sit down, get a coffee and get ready for some math.

Hoeffding's Inequality

Consider the following.

Let $X_1, _{\cdots}, X_n$ be a set of identical and independently distributed (i.i.d) random variables in [0, 1] with a true mean $\mu = \mathbb{E}[X]$, and let $\overline{X}t = \frac{1}{n}\sum^n{i=1}X_i$ define the sample mean. Hoeffding's inequality allows us to consider how far off the sample mean is from the true mean of the random variable. Such that

$$ p(\overline{X}_n + u \le \mu) \le e^{-2nu^2} $$

The probability of our sample mean, plus some value $u$ being less than the true mean $\mu$ is bound by value $e^{-2nu^2}$. This has some intuition, as the value of $n$ climbs (the more samples we take) or as $u$ increases (we just make it a bigger number) the value will decrease, as we will less and less likely we are less than the true mean.

We can apply Hoeffding's inequality to the bandit problem.

Where the sample mean $\overline{X}_n$ is our action value estimate $Q_t(a)$. The value $u$ is our confidence of our action value estimate $U_t(a)$. The true mean $\mu$ is the true action value $q(a)$.

$$ p(Q_t(a) + U_t(a) \le q(a) ) \le e^{-2N_t(a) U_t(a)^2} $$

We want to pick the bound $e^{-2N_t(a) U_t(a)^2}$ to be small, such that the probability that the true mean being more than the bound $U_t$ away from our estimate mean is probability $p$. Lets pick a small probability $p$.

$$ e^{-2N_t(a) U_t(a)^2} = p $$

We then solve for $U_t(a)$ which allows us to determine how to compute our confidence:

$$ U_t(a) = \sqrt{\frac{-log \space p}{2N_t(a)}} $$

Now lets set $p$ to be a small value, and allow it to decrease over time, for example $p=1/t$ which when plugged into the bound, we get:

$$U_t(a) = \sqrt{\frac{log \space t}{2N_t(a)}}$$

There are other values for $p$ but we are going to use this one.

Furthermore, we can remove the 2 from the denominator and start to treat it as a hyper-parameter $c$, for example.

$$ a_t = \underset{a \in A}{\arg\max} Q_t(a) + c \sqrt{\frac{log \space t}{N_t(a)}} $$

If c is larger, we will explore more, if c is smaller we will explore less. In the code (see update_confidence function in the UCBAgent) I have set this as default to 2, feel free to explore different values for $c$ and see how it affects the performance.

2.2.6 Thompson Sampling

Thompson Sampling implements Bayesian updating in order to select actions, it is a simple computation but it works really well! In the experiments I have run, it will constantly outperform the UCB and $\epsilon$-Greedy algorithm. It is also worth noting how old Thompson Sampling is, it was produced in 1933.

Thompson Sampling selects its actions according to our belief that the action is the optimal action. To understand Thompson Sampling, I need to walk you through the Bayesian approach at multi-armed bandits and probability matching, as both of these topics should help our understanding of the Thompson Algorithm.

The Bayesian Approach

With the Bayesian approach, we are modeling distributions over the values $p(q(a) | \theta)$, we are trying to model the distribution of expected rewards we get for each action and update our distribution accordingly. The probability that we compute should be interpreted as the belief that $q(a) = x$. Theta is the parameters of the model, for example $\theta$ might contain the means and variances of the distributions if we were using Gaussian distributions.

Using these posterior distributions, we can guide which actions should be taken.

Probability Matching.

In probability matching, we select action $a$ according to what we believe is the best action. This policy is stochastic and is denoted as such:

$$ \pi_t(a) = p(q(a) = \max_{a'}q(a') \space | \space H_{t-1}) $$

Where $H_{t-1}$ is the probability distribution at time step $t-1$, because we have these probability distributions we can reason about which action could be the most optimal action. This policy is also optimistic in the face of uncertainty as actions will be selected either if they have a high value estimate, or we are really uncertain. For some intuition, if we are really uncertain of an action, the distribution we for that action should be really wide. However, it can be difficult to compute a policy analytically from these posterior distributions, so there is where Thompson Sampling comes in.

Thompson Sampling.

In Thompson Sampling, we still keep track of the posterior distributions of each action, and we will use these distributions to sample an actual action value. We sample each distribution for each action, giving us an action value for each action.

We then select action according to:

$$ A_t = \underset{a \in A}{\arg\max}Q_t(a) $$

If we follow this, Thompson Sampling will have a policy as such:

$$ \text{Thompson Sampling} = \pi_t(a) = \mathbb{E}\left[ \space I(Q_t(a) = \max_{a'}Q_t(a'))\space \right] $$

Note that this is the exact same as probability matching.

$$ \text{Probability Matching} = \pi_t(a) = \left(q(a) = \max_{a'} q(a')\right) $$

But using Thompson Sampling we do not have to compute the probabilites of each action being taken. We simply just sample the distributions and pick our actions greedily.

Thing of Thompson Sampling as a way of using the posterior distributions for each action to select and action we can take.

In the code, the prior distribtuions for each action is a uniform distribution between [0,1], and the posterior distributions are beta distributions with the parameters $a = 1$ and $b = 1$. Every time we receive a reward of 1, we increment the $a$ parameter by 1. If the reward is 0 we increment the $b$ parameter by 1. We then choose our actions using Thompson Sampling, sampling each of the distributions and greedily choosing our actions.

I am quite a visual learner, this website really helped me understand how changing the alpha and beta parameters of our posterior distributions effects the samples we will get from it. I encourage you to go here and play around with the values and understand how incrementing the values in the posterior distribution will allow us to select optimal actions.

Softmax

The softmax approach to the multi-armed bandit problem takes into account the Q values of each action, sampling an action from a distribution that is proportional to each actions value. This is such that actions with higher Q values have a higher probability of being chosen.

Softmax has an important hyperparameter called temperature, this is denoted with $ \tau $ (tau). This controls the algorithms sensitivity to differences in the Q values of each action. If $ \tau $ is approaching infinity, then all actions will be sampled from a uniform distribution. If $ \tau $ is approaching 0, then the action with the highest Q value will be selected with probability 1. Although in practice, researchers tend to just use really big or really small positive numbers as you will see below with the policy for Softmax we need to divide by $ \tau $ making 0 an impractical number. Much like $\epsilon$-greedy, we can also decay temperature such that the algorithm explores more actions at the start, exploiting the knowledge it has gained towards the end of the iterations. However, in my implementation, I have kept temperature constant, and it appears to perform really well!

The policy of the Softmax algorithm is such:

$$ \pi(a) = \frac{\exp\left( \frac{Q(a)}{\tau}\right)}{\sum_{b=0}^B \exp \left( \frac{Q(b)}{\tau} \right)} $$

Optimistic Initialization

Optimistic Initialization is a rather simple but effective approach to multi-armed bandits. I like to think of it as the Greedy algorithms clever sibling. Much like the greedy algorithm, Optimistic Initialization selects its actions by choosing the action with the highest Q value estimate at that iteration. Where it differs, is the set up of the problem itself.

When initializing the agent, instead of setting all Q values to 0, we set them to the highest reward possible (in this implementation I am using Bernoulli bandits so it is 1). Alongside the Q values, we also initialize the counts to a higher value. Why? Well as the algorithm starts to select actions, it will be consistently disappointed with the results it is getting, which will reduce the Q value of that action. But since all of the actions have been initialized to high values, the agent will go and explore another action, this repeats until the agent settles on the action with the highest source of reward. Initializing the Q value to a high number encourages the agent to explore actions that have not been explored enough.

The more the agent selects an action, the close and closer it will converge to its true value. Eventually, Optimistic Initialization will end up on the best option.

It is worth noting that we need to know the highest reward possible in the environment if we want to get this correct. This is a downside of using this algorithm, if the MDP was not available to use (it is here) we would not be able to use Optimistic Initialization effectively. If we set the value too high, we do not converge quickly enough on the correct action, if we set it too low, the algorithm will no longer be "optimistic" about the Q values so will not work.

Furthermore, setting the counts to a higher value is a representation of our uncertainty about the estimate, we find the optimal counts bonus with tuning, but we are having to place our cards down on the table at the start of each experiment which is impractical, we would much rather compute uncertainty about our estimates on the fly, like in the UCB algorithm.

Conclusion.

There we have it, we have explored quite a lot in this final project. We have spoken about multi-armed bandits, the environment for them, and the algorithms that aim to solve them. Hopefully you now feel confident enough to go through my code and see how I have implemented all of these algorithms. This repo is not aimed to make it the most efficient, I instead wanted to show that how these algorithms work and implement my first project in reinforcement learning. I hope you enjoy!!!

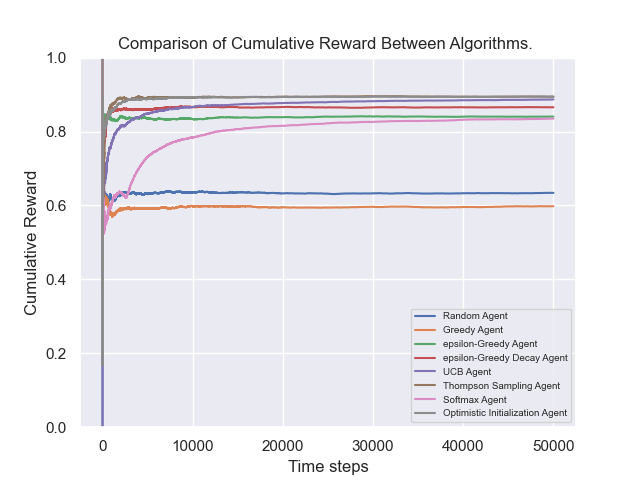
Here is the figure of the cumulative reward of each agent from an experiment I ran using this code, there are many more in the plotting code, but this give the best overview of each algorithms performance.

References

DeepMind x UCL Lectures - Lectures 1 and 2 helped my mathematical and theoretical understanding of RL, multi-armed bandits and the algorithms.
Alejandro Aristzabal - Has a great series on the multi-armed bandit problem, with code.
Edward Pie - Great explanation with some example code.
Mattia Cinelli - Has a really detailed repo of RL examples, great to look at for multi armed bandits and beyond.
Lilian Wang - Blog on the maths behind the algorithms, there is also some code she has written for an implementation of the problem.
Deep Reinforcement Learning - A great book for RL, I am currently going through it.

Cam-Wheeler/CS50_Final_Project