This project provides a solver for a N-Puzzle Game.
The game rules can be found here: http://mypuzzle.org/sliding
- Python 3.X
- No library needed
- Linux (It can works on Windows by deleting the resource library)
Note: The use of numpy could simplify and accelerate the steps of the algorithm. But we wanted to create a simple algorithm here without any extra library.
Run the test by launching the following code :
$ python3 driver.py "method" "board"
Where "method" can be :
- "bfs" : Breadth-First Search.
- "dfs" : Depth-First Search
- "ast" : A-Star Search.
"board" define the position of numbers inside the board:
- It must be a "m*m" board with "m" a positive integer
- the position of the zero define the empty tile
- all numbers must be separated by a comma
When executed, the program will create/write to a file called output.txt, containing the following statistics:
path_to_goal: the sequence of moves taken to reach the goal
cost_of_path: the number of moves taken to reach the goal
nodes_expanded: the number of nodes that have been expanded
search_depth: the depth within the search tree when the goal node is found
max_search_depth: the maximum depth of the search tree in the lifetime of the algorithm
running_time: the total running time of the search instance, reported in seconds
max_ram_usage: the maximum RAM usage in the lifetime of the process as measured by the ru_maxrss attribute in the resource module, reported in megabytes
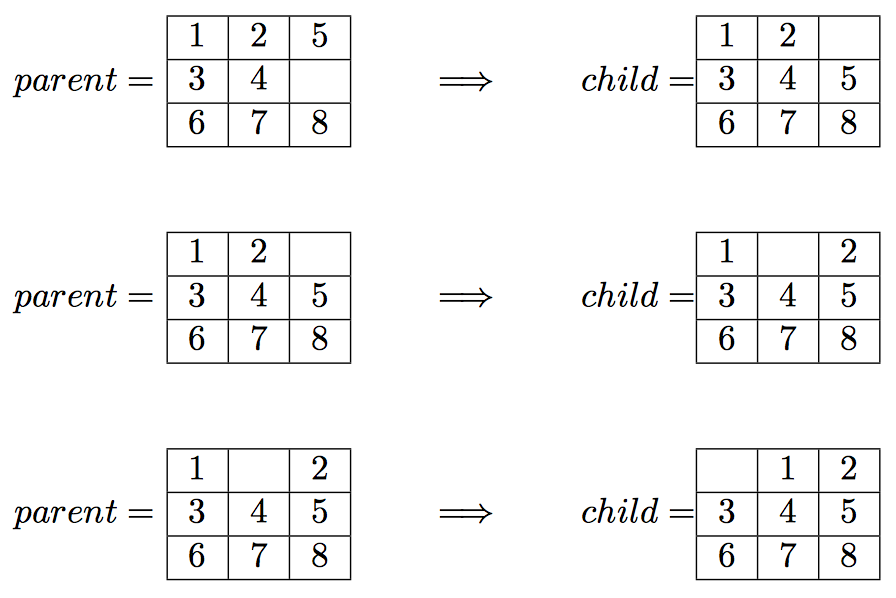
$ python3 driver.py bfs 1,2,5,3,4,0,6,7,8
The grid here is of size 3x3 = 9
The path followed by the algorithm would be:
The output file (example) will contain exactly the following lines:
path_to_goal: ['Up', 'Left', 'Left']
cost_of_path: 3
nodes_expanded: 10
search_depth: 3
max_search_depth: 4
running_time: 0.00188088
max_ram_usage: 0.07812500
BFS: https://en.wikipedia.org/wiki/Breadth-first_search
DFS: https://en.wikipedia.org/wiki/Depth-first_search
A-star: https://en.wikipedia.org/wiki/A*_search_algorithm
We used the Manhattan distance as an heuristic function.
It corresponds to the sum of the distances of the tiles from their goal positions.
Christian Tchou