Title: Jump-Diffusion Models for Financial Bubbles Modelling: A Multi-scale Type-II Bubble Model With Self-Excited Crashes
For citations in biblatex:
@article{CarKotJumpDiffusionThesis,
author = "Cariou-Kotlarek, Niels",
title = "Jump-Diffusion Models for Financial Bubbles Modelling: A Multi-scale Type-II Bubble Model With Self-Excited Crashes",
year = "2022",
month = "09",
publisher = "ETH Zurich Working Paper Preprint",
url = "https://github.com/Code-Cornelius/jump_diff_bubble_II_thesis"}
This repository gathers the work I have done during my master's thesis at ETH Zurich in 2022. This thesis was published in September 2022 as part of the completion of my degree in applied mathematics. I had the opportunity to join Prof Sornette's research group and I have worked on financial bubbles where we have developed a new bubble model of type-II. All the technical details are explained inside the thesis.
The thesis is in a PDF format at the root of this repository under the
name fin_bubbles_model_masters_thesis_carioukotlarek.pdf.
Abstract: The thesis contributes to the ongoing efforts to develop more accurate and effective models of financial bubbles. We present a novel approach to modelling financial bubbles by developing a type-II bubble model aiming at presenting both positive and negative bubble episodes. We achieve this by considering a process with features such as positive feedback, self-excitation effects, non-stationary dynamics as well as multiple regimes, integral to the complex interactions in modern, computerized markets. The first part of the thesis outlines a novel extension of the integer-valued autoregressive process from its univariate form to the multidimensional setting. This extension serves as the underpinning for the proposed bubble model. Specifically, we introduce the INVAR process as a generalisation of the integer-valued autoregressive process (INAR) to the multivariate domain to discretise the Hawkes processes used in the bubble model. In the second part, known stylized facts of financial markets are discussed, and we explain the use of temporal point processes and rough models in finance. The third part presents a first step in constructing type-II bubble model and compares it to current literature, highlighting its unique features, such as the use of a bivariate Hawkes process that has both upward and downward jumps, a multi-scale mispricing index and a regime process. The analysis reveals that adding opposite sign Hawkes processes is not a promising approach to bubble modelling, however some of the tools we developed could be useful to improve existing bubble models.
In this repository, one will find the code used to perform the experiments of the thesis.
A folder containing miscellaneous experiments for debugging purposes or to generate the plots that populate the thesis.
experiments/data_exploration contains the scripts for the plots related to data exploration as stored in data.
experiments/delayed_compensation contains the scripts for the plots related to delayed
compensation (src/stock_bubble/delay_compens.py) experiments.
ACF_bm.py and signal_processing.py compute some measurements about time series.
kernels_approx.py displays the approximation errors of certain kernels choices.
market_impact.py create the plot showing the shape of market impact as calculated by Rosenbaum et al. in Paul Jusselin
and Mathieu Rosenbaum. “No-arbitrage implies power-law market impact and rough volatility”.
compar_mispricing_byhand_approx.py compares the mispricing approximated with the exact one.
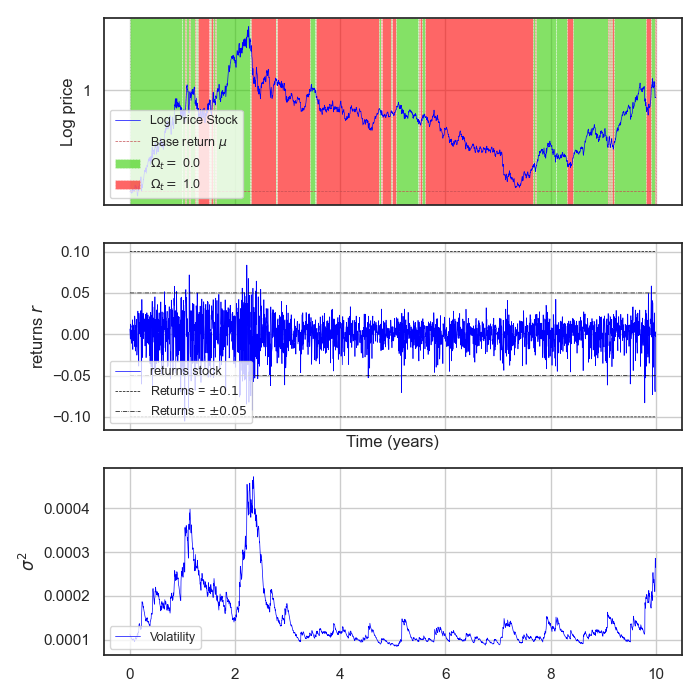
In the source code we have a file where the simulation of bubbles happen: simul_bubble_script. From it, it is possible
to sample both type-I and II bubbles. See one example of a trajectory:
All files related to INVAR are accessible on the repository of the working
paper: https://github.com/Code-Cornelius/invar_process_estimation.