This repository contains Python scripts for the simulation of CT data acquisition and for CT reconstruction. The ct_toolbox.py file contains all reusable functions and the fbp_example.py and least_squares_example.py files show how this functionality can be used to reconstruct a CT image in 2 different ways: matrix inversion and filtered back projection.
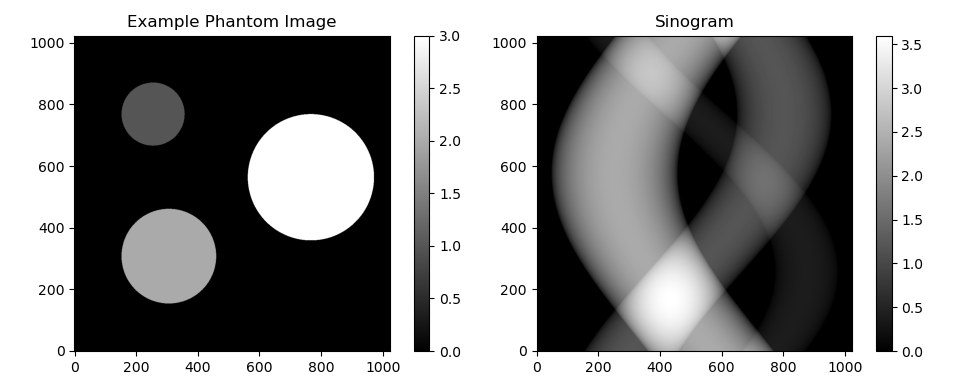
To simulate the acquisition of CT data the user can define a phantom consisting of nonoverlapping circles. From this continuous representation images can be generated at any resolution. By projecting the data stepwise in all directions a sinogram is created, where every row represents one projection. In this repository I always assume that parallel beams are used and that the source and detector are at a distance of 1 from the origin, resulting in a circle shaped reconstruction area. For ease of computation the calculations and plotting are done in a square region around this circle. However, only the results within the inscribed circle of this square should be considered when assessing the quality of the results.
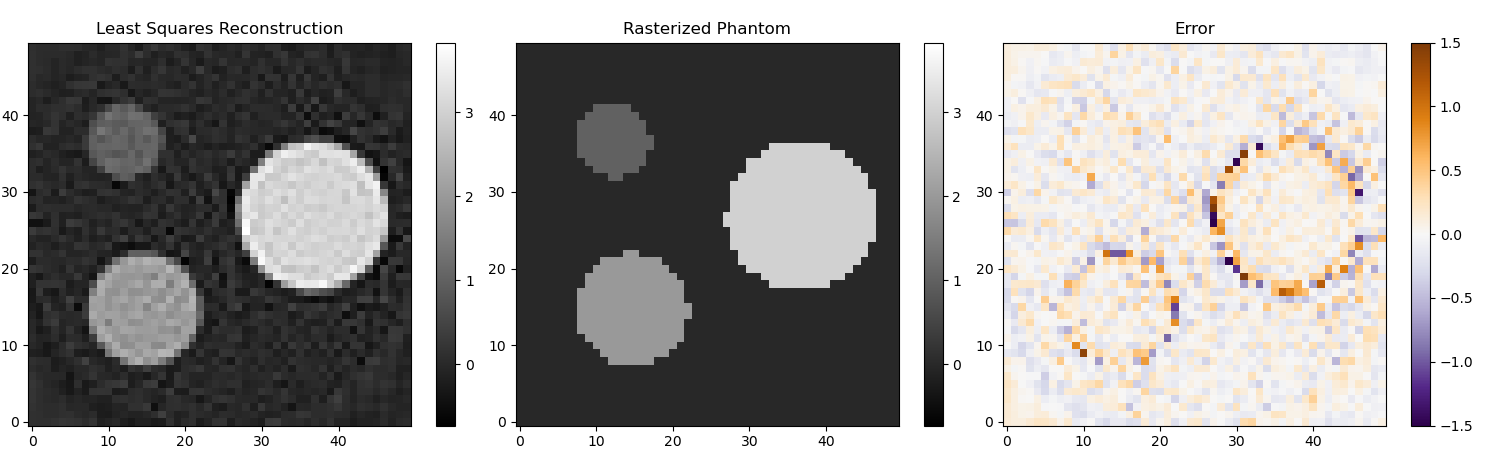
The process of calculating the projections from a given image can be modelled as a linear process: Ax = y, where x is a vector representing the image and y is a vector representing the sinogram. In a typical reconstruction setting y is measured and A can be derived from the setup, so x can be calculated by solving the equation for x in the least squares sense. Imaging problems are often very unstable, which is means that a small error in y or A can cause a large error in the solution for x. Any approach that changes the problem to make it less unstable is called a regularization. The way I calculated forward matrix A is slightly different from the way I calculated the sinogram, so some regularization is required to make sure this small mismatch doesn't cause a big error in the solution x.
A very general approach to regularization is to use the singular value decomposition (SVD) of matrix A. In simplified terms the SVD determines in which directions a small change in x can cause a big change in y and vice versa. Small singular values correspond to directions where a small change in y can cause a large change in x. By removing all singular values below a threshold from the SVD you can create a new matrix A' that is more stable. That matrix is never fully constructed in practice because the SVD is also a useful form for solving the least squares problem. The numpy function numpy.linalg.lstsq does both the thresholding and the inversion. In my example it is configured to discard all singular values that are smaller than 0.075 times the largest singular value.
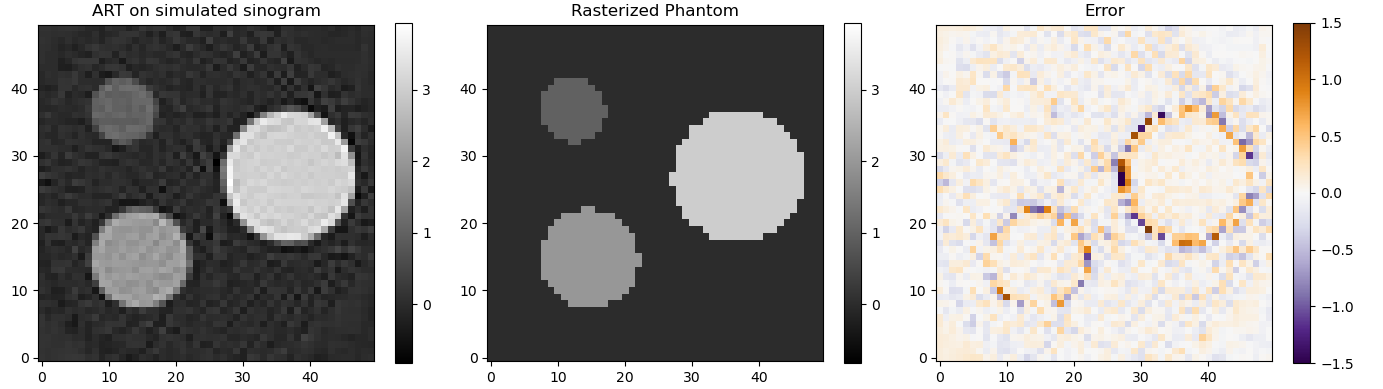
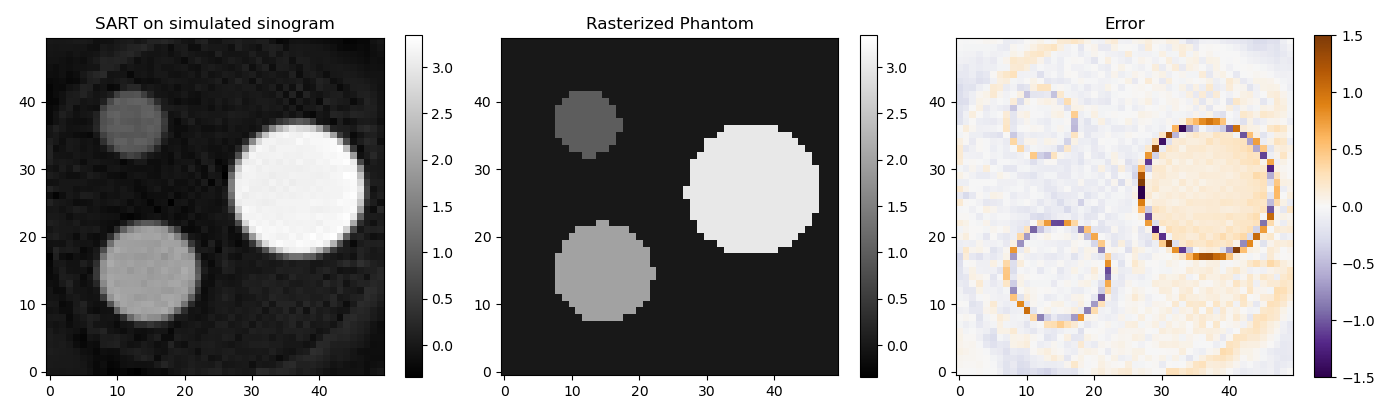
Because matrix A has dimensions all pixels in the reconstruction x all pixels in the sinogram it can grow very quickly. That's also why I showed such a low resolution example. There are algorithms such as ART and SART that solve the same equation without needing the whole matrix to be in memory.
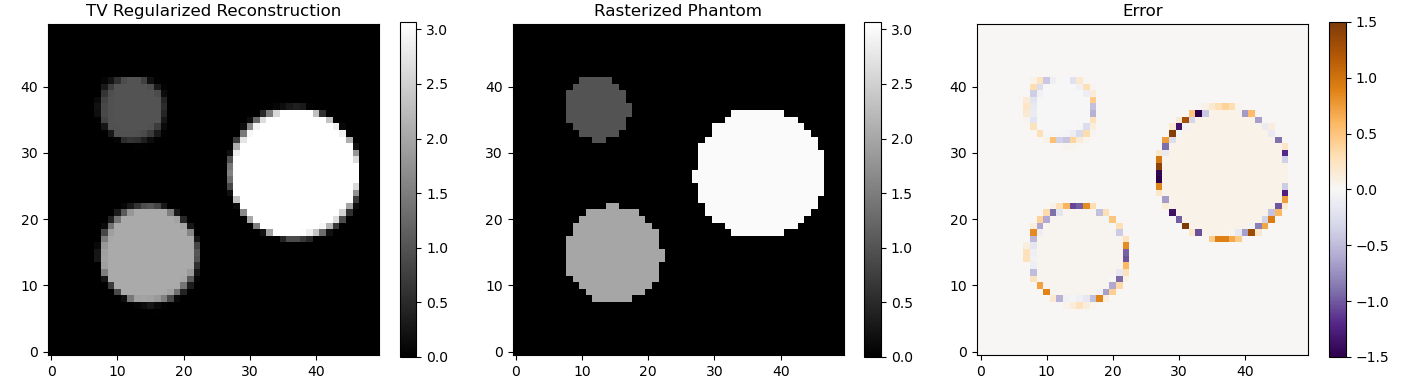
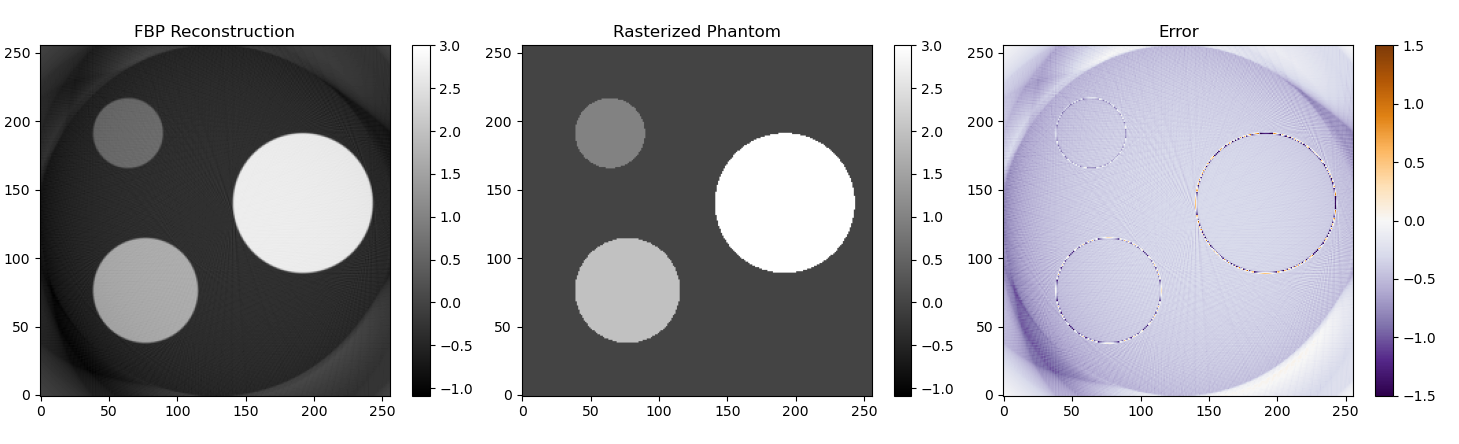
Another technique to reconstruct a CT image is filtered back projection. In this technique the sinogram is filtered using a Ram Lak filter (high pass ramp filter) and every projection (row of the sinogram) is smeared back over the image in the same direction it was acquired. Using the implementation in this repository I got the following results.
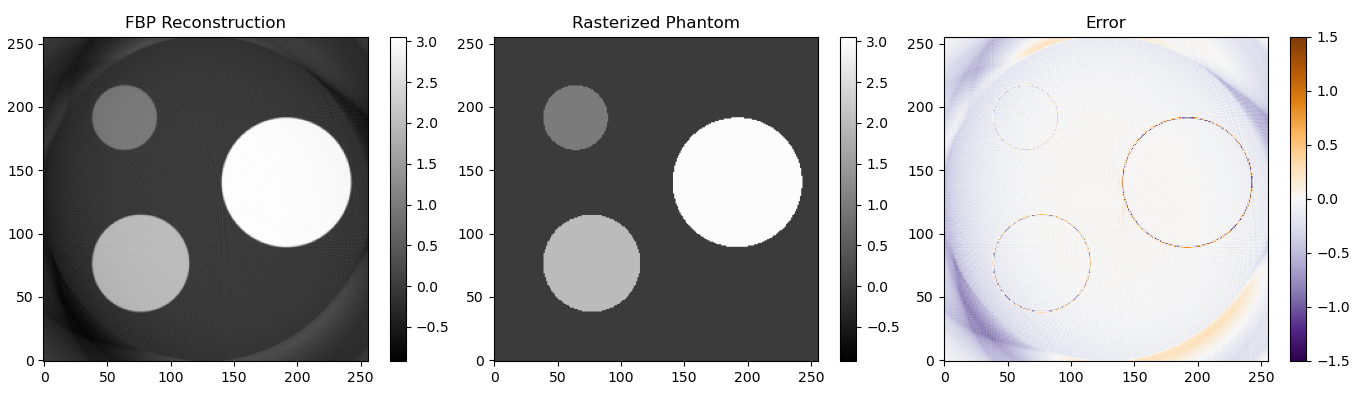
In the image above I used a straightforward ramp filter. As you can see the overall shape is reconstructed correctly, but most of the image is slightly underestimated. By looking at the implementation of filtered back projection in the Scikit-Image library I found out that they used a slightly smarter filter. I also made the filter from Scikit-Image available in my code. With that filter most of the image is correctly reconstructed.
For more information on this filter you can have a look at the Scikit-Image source code or at chapter 3 of the book they mentioned as a reference: http://www.slaney.org/pct/pct-toc.html.