QP Solvers for Python

Unified interface to Quadratic Programming (QP) solvers available in Python.

Installation

pip install qpsolvers

Check out the documentation for Python 2 or Windows instructions.

Usage

The library provides a one-stop shop solve_qp(P, q, G, h, A, b, lb, ub) function with a solver keyword argument to select the backend solver. It solves convex quadratic programs in standard form:

Vector inequalities are taken coordinate by coordinate. For most solvers, the matrix P should be positive definite.

Example

To solve a quadratic program, build the matrices that define it and call the solve_qp function:

from numpy import array, dot
from qpsolvers import solve_qp

M = array([[1., 2., 0.], [-8., 3., 2.], [0., 1., 1.]])
P = dot(M.T, M)  # this is a positive definite matrix
q = dot(array([3., 2., 3.]), M).reshape((3,))
G = array([[1., 2., 1.], [2., 0., 1.], [-1., 2., -1.]])
h = array([3., 2., -2.]).reshape((3,))
A = array([1., 1., 1.])
b = array([1.])

x = solve_qp(P, q, G, h, A, b)
print("QP solution: x = {}".format(x))

This example outputs the solution [0.30769231, -0.69230769, 1.38461538].

Solvers

The list of supported solvers currently includes:

Dense solvers:
- CVXOPT
- qpOASES
- quadprog
Sparse solvers:
- ECOS
- Gurobi
- MOSEK
- OSQP
- SCS

Frequently Asked Questions

Can I print the list of solvers available on my machine?
- Absolutely: print(qpsolvers.available_solvers)
Is it possible to solve a least squares rather than a quadratic program?
- Yes, qpsolvers also provides a solve_ls function.
I have a squared norm in my cost function, how can I apply a QP solver to my problem?
- You can cast squared norms to QP matrices and feed the result to solve_qp.
I have a non-convex quadratic program. Is there a solver I can use?
- Unfortunately most available QP solvers are designed for convex problems.
- If your cost matrix P is semi-definite rather than definite, try OSQP.
- If your problem has concave components, go for a nonlinear solver such as IPOPT e.g. using CasADi.
I get the following build error on Windows when running pip install qpsolvers.
- You will need to install the Visual C++ Build Tools to build all package dependencies.

Performances

On a dense problem, the performance of all solvers (as measured by IPython's %timeit on an Intel(R) Core(TM) i7-6700K CPU @ 4.00GHz) is:

Solver	Type	Time (ms)
quadprog	Dense	0.01
qpoases	Dense	0.02
osqp	Sparse	0.03
scs	Sparse	0.03
ecos	Sparse	0.27
cvxopt	Dense	0.44
gurobi	Sparse	1.74
cvxpy	Sparse	5.71
mosek	Sparse	7.17

On a sparse problem with n = 500 optimization variables, these performances become:

Solver	Type	Time (ms)
osqp	Sparse	1
scs	Sparse	4
cvxpy	Sparse	11
mosek	Sparse	17
ecos	Sparse	33
cvxopt	Dense	51
gurobi	Sparse	221
quadprog	Dense	427
qpoases	Dense	1560

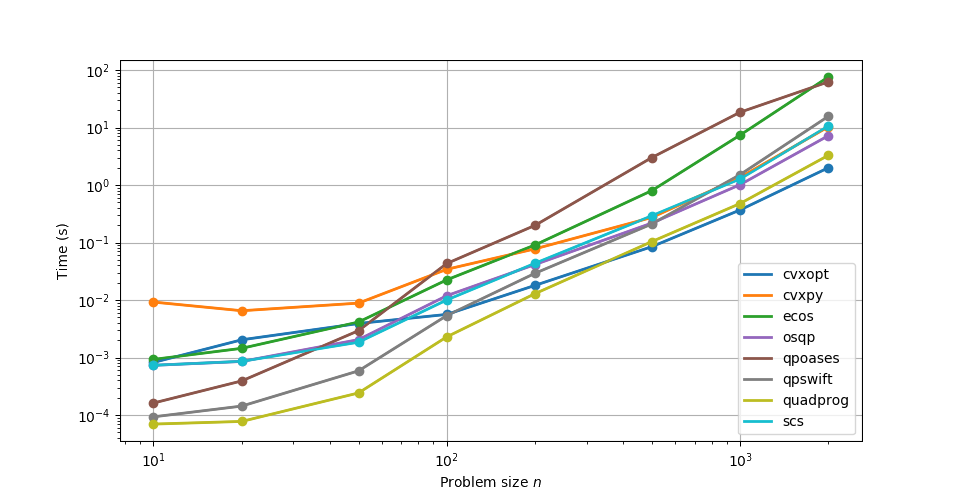
Finally, here is a small benchmark of random dense problems (each data point corresponds to an average over 10 runs):

Note that performances of QP solvers largely depend on the problem solved. For instance, MOSEK performs an automatic conversion to Second-Order Cone Programming (SOCP) which the documentation advises bypassing for better performance. Similarly, ECOS reformulates from QP to SOCP and works best on small problems.