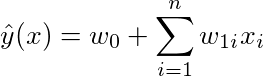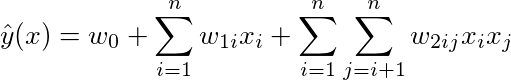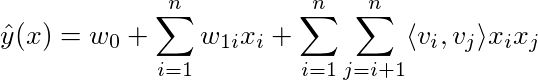A library for factorization machines in pytorch. A factorization machine is like a linear model, except multiplicative interaction terms between the variables are modeled as well.
The input to a factorization machine layer is a vector, and the output is a scalar. Batching is fully supported.
This is a work in progress. Feedback and bugfixes welcome! Hopefully you find the code useful.
The factorization machine layers in fmpytorch can be used just like any other built-in module. Here's a simple feed-forward model using a factorization machine that takes in a 50-D input, and models interactions using k=5 factors.
import torch
from fmpytorch.second_order.fm import FactorizationMachine
class MyModel(torch.nn.Module):
def __init__(self):
super(MyModel, self).__init__()
self.linear = torch.nn.Linear(100, 50)
self.dropout = torch.nn.Dropout(.5)
# This makes a fm layer mapping from 50-D to 1-D.
# The number of factors is 5.
self.fm = FactorizationMachine(50, 5)
def forward(self, x):
x = self.linear(x)
x = self.dropout(x)
x = self.fm(x)
return x
See examples/toy.py or examples/regression.py for fuller examples.
This package requires pytorch, numpy, and cython.
To install, you can run:
cd fmpytorch
sudo python setup.py install
A linear model, given a vector x models its output y as
where w are the learnable weights of the model.
However, the interactions between the input variables x_i are purely additive. In some cases, it might be useful to model the interactions between your variables, e.g., x_i * x_j. You could add terms into your model like
However, this introduces a large number of w2 variables. Specifically, there are O(n^2) parameters introduced in this formulation, one for each interaction pair. A factorization machine approximates w2 using low dimensional factors, i.e.,
where each v_i is a low-dimensional vector. This is the forward pass of a second order factorization machine. This low-rank re-formulation has reduced the number of additional parameters for the factorization machine to O(k*n). Magically, the forward (and backward) pass can be reformulated so that it can be computed in O(k*n), rather than the naive O(k*n^2) formulation above.
Currently, only a second order factorization machine is supported. The forward and backward passes are implemented in cython. Compared to the autodiff solution, the cython passes run several orders of magnitude faster. I've only tested it with python 2 at the moment.
- Support for sparse tensors.
- More interesting useage examples
- More testing, e.g., with python 3, etc.
- Make sure all of the code plays nice with torch-specific stuff, e.g., GPUs
- Arbitrary order factorization machine support
- Better organization/code cleaning
Vlad Niculae (@vene) for his sage wisdom.
The original factorization machine citation, which this layer is based off of, is
@inproceedings{rendle2010factorization,
title={Factorization machines},
author={Rendle, Steffen},
booktitle={ICDM},
pages={995--1000},
year={2010},
organization={IEEE}
}