Exploring Differential Geometry in Neural Implicits

Tiago Novello [1], Guilherme Schardong [3], Luiz Schirmer [3], Vinícius da Silva [2], Hélio Lopes [2], Luiz Velho [1]
[1] Institute for Pure and Applied Mathematics (IMPA), [2] Pontifical Catholic University of Rio de Janeiro (PUC-Rio), [3] University of Coimbra (UC)

This is the official implementation of "Exploring Differential Geometry in Neural Implicits".

Get started

Prerequisites

Anaconda, alternativelly you can use PyEnv and PyEnv-VirtualEnv on UNIX based/like systems
Git
Integrate Git Bash with conda (If on Windows)
MeshLab

Code organization

dataset.py - contains the sampling and data classes
diff_operators.py - implementation of differential operators (gradient, hessian, jacobian, curvatures)
loss_functions.py - contains loss functions for different experimental settings
main.py - main function and point-of-entry to our code
meshing.py - mesh creation through marching cubes
model.py - network and layers implementations
util.py - miscelaneous functions and utilities

Additionally, under the experiment_scripts folder, there are three scripts with experiments and other auxiliary code that is generally independent of the main code.

comparison_analytic.py - comparison experiments of RBF, SIREN and our approach for analytic models of a sphere and torus
comparison_ply.py - comparison experiments of RBF, SIREN and our approach for PLY models
mesh2sdf_open3d_performance_test.py - performance test using SDF querying implemented in mesh2sdf and open3d. Not used in the paper, only testing if it was worth replacing the sampling code implemented using mesh2sdf with open3d.

In the tools folder, there are two scripts:

estimate_mesh_curvatures.py: Given a trained model (pth) and the original mesh, we estimate the vertex curvatures using the trained model.
reconstruct.py: Given a trained model (pth) reconstructs the mesh using marching cubes.

Setup and sample run

Open a terminal (or Git Bash if using Windows)
Clone the repository: git clone git@github.com:dsilvavinicius/differential_geometry_in_neural_implicits.git i3d.
Enter project folder: cd i3d.
Create the environment and setup project dependencies:

conda env create -f environment.yml
conda activate i3d
pip install -e .

or, if using pyenv (with pyenv-virtualenv):

pyenv virtualenv 3.9.9 i3d
pyenv local i3d
pip install -r requirements
pip install -e .

Download the datasets (available here) and extract them into the data folder of the repository
Train a network for the armadillo mesh:

python main.py experiments/armadillo_curvature_batch_sdf.json

The results will be stored in results/armadillo_biased_curvatures_sdf.
To visualize the output mesh by opening the output PLY using MeshLab:

meshlab results/armadillo_biased_curvatures_sdf/reconstructions/model_best.ply

End Result

If everything works, MeshLab should show the following image (or an image similar to it):

Linux

We tested the build steps stated above on Ubuntu 20.04. The prerequisites and setup remain the same, since all packages are available for both systems. We also provide a Makefile to cover the data download and network training and visualization (steps 5 through 8) above.

Running on a headless server

If you are training your model in a remote server with no graphical environment, you will probably end up with the following error: pyglet.canvas.xlib.NoSuchDisplayException: Cannot connect to "None". This will happen during the sampling step when loading a mesh. Basically, this means that pyglet needs a graphical display, which does not exist. You can work around this error by creating a virtual framebuffer, which can be done by prepending your python command with: xvfb-run -s "-screen 0 1400x900x24", as in:

xvfb-run -s "-screen 0 1400x900x24" python main.py experiments/armadillo_sdf.json

Citation

If you find our work useful in your research, please cite:

@article{novello:i3d:2022,
  title = {Exploring differential geometry in neural implicits},
  journal = {Computers & Graphics},
  volume = {108},
  pages = {49-60},
  year = {2022},
  issn = {0097-8493},
  doi = {https://doi.org/10.1016/j.cag.2022.09.003},
  url = {https://www.sciencedirect.com/science/article/pii/S0097849322001649},
  author = {Tiago Novello and Guilherme Schardong and Luiz Schirmer and Vinícius {da Silva} and Hélio Lopes and Luiz Velho},
  keywords = {Implicit surfaces, Neural Implicits, Neural Networks, Curvatures},
}

Contributors

Besides the paper authors, we list other contributors below. Thank you for helping make our code better!

DavidXu-JJ - Handling the U=W=0 case on diff_operators.principal_directions

Contact

If you have any questions, please feel free to email the authors, or open an issue.

Other examples

Principal curvatures and directions overlaid on the Armadillo.

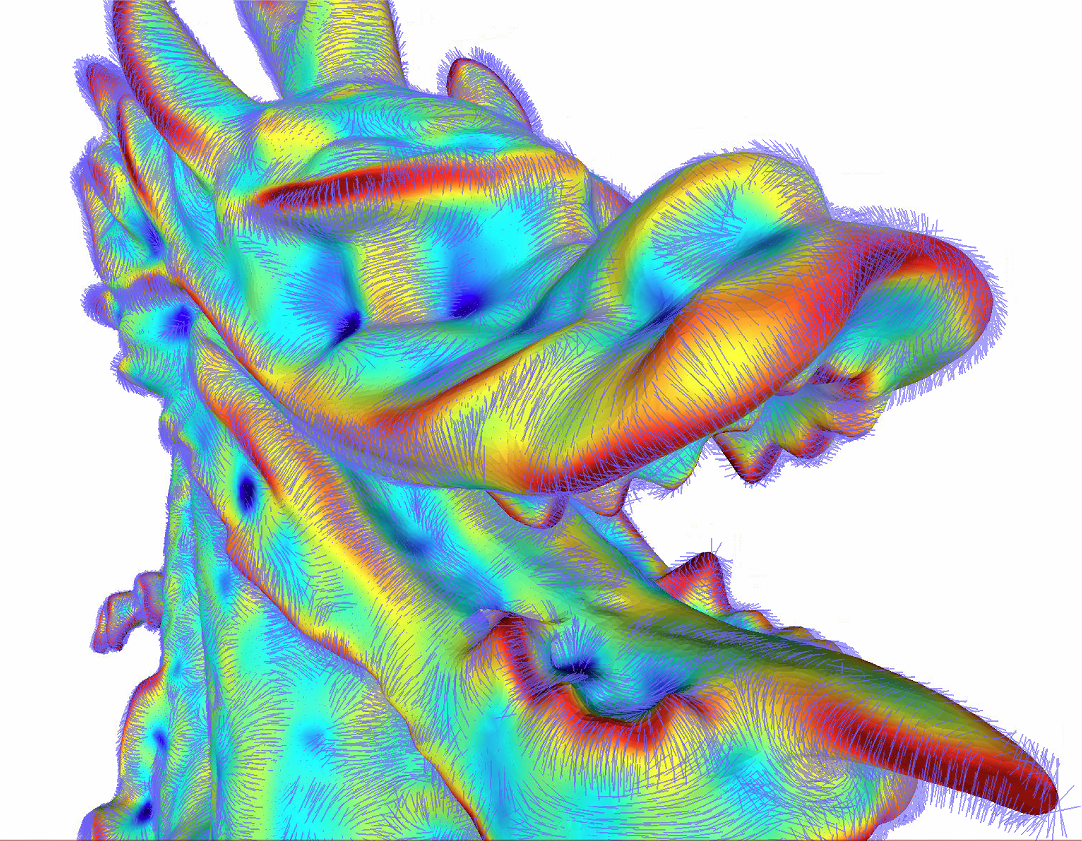Maximum curvature and corresponding direction on the Stanford Dragon.

DavidXu-JJ/differential_geometry_in_neural_implicits