You can also find all 53 answers here 👉 Devinterview.io - Recursion Algorithm
Dynamic Programming (DP), Recursion, and Memoization are techniques for solving problems that can be divided into smaller, overlapping sub-problems. While they share this commonality, they each offer unique advantages and limitations.
-
Efficiency: DP typically leads to polynomial-time algorithms, whereas Recursion and Memoization can result in higher time complexities.
-
Problem-Solving Direction: DP builds solutions from the ground up, focusing on smaller sub-problems first. In contrast, Recursion and Memoization usually adopt a top-down approach.
-
Implementation Style: DP and Memoization can be implemented either iteratively or recursively, while Recursion is, by definition, a recursive technique.
-
Sub-Problem Coverage: DP aims to solve all relevant sub-problems, whereas Memoization and Recursion solve sub-problems on an as-needed basis.
-
Memory Use: DP often requires less memory than Memoization, as it doesn't store every state reached through recursive calls.
Let's look into some examples and see how they utilize the core concepts of recursion.
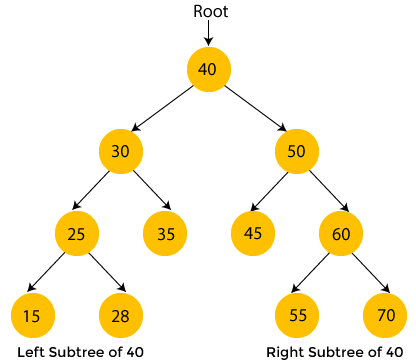
In binary tree traversal, nodes are visited recursively, exploring the left and right subtrees in various orders.
class Node:
def __init__(self, value):
self.value = value
self.left = None
self.right = None
def in_order_traversal(node):
if node is not None:
in_order_traversal(node.left)
print(node.value)
in_order_traversal(node.right)A palindrome is a word, phrase, number, or other sequence of characters that reads the same forward and backward. To determine a palindrome, the outer characters of a word are compared. If they match, the inner substring is checked recursively.
def is_palindrome(word):
if len(word) <= 1:
return True
if word[0] == word[-1]:
return is_palindrome(word[1:-1])
return FalseThe factorial of a number is calculated using a base and recursive case.
def factorial(n):
if n == 0:
return 1
return n * factorial(n-1)A folder hierarchy in a file system can be traversed recursively, exploring the contents of each directory.
import os
def folder_contents(path):
for item in os.listdir(path):
item_path = os.path.join(path, item)
if os.path.isfile(item_path):
print(f"Found a file: {item_path}")
elif os.path.isdir(item_path):
print(f"Entering folder: {item_path}")
folder_contents(item_path)The Towers of Hanoi is a mathematical puzzle that involves three pegs and a set of disks of different sizes, which can be moved from one peg to another following a set of rules. It's often used as an example in computer science textbooks to illustrate how recursion can be used to solve problems.
def tower_of_hanoi(n, source, target, auxiliary):
if n == 1:
print(f"Move disk 1 from {source} to {target}")
return
tower_of_hanoi(n-1, source, auxiliary, target)
print(f"Move disk {n} from {source} to {target}")
tower_of_hanoi(n-1, auxiliary, target, source)This sorting algorithm follows the divide-and-conquer paradigm, using recursion to split and then merge lists.
def merge_sort(arr):
if len(arr) <= 1:
return arr
mid = len(arr) // 2
left_half = arr[:mid]
right_half = arr[mid:]
left_half = merge_sort(left_half)
right_half = merge_sort(right_half)
return merge(left_half, right_half)The Catalan numbers form a sequence of natural numbers that occur in various counting problems, often involving recursive structures. The recursive formula for the
where the base case is
Backtracking often employs recursion to explore the vast space of possible solutions. However, not all recursive algorithms involve backtracking.
Think of recursion as the mechanism that enables a function to call itself, and backtracking as a strategy where you make a choice and explore the possibilities.
-
Recursion: Utilizes a divide-and-conquer approach, breaking the main problem into smaller, self-similar subproblems. Recursive calls work towards solving these subproblems, relying on defined base cases for termination.
-
Backtracking: Operates as an advanced form of recursion by building solutions incrementally. When a partial solution is deemed unsuitable, it "backtracks" to modify previous choices, ensuring an efficient traversal through the solution space.
- Tree Traversals: Visiting all nodes in a tree, like in binary search trees.
- Divide and Conquer Algorithms: Such as merge sort or quick sort.
- Dynamic Programming: Solving problems like the coin change problem by breaking them down into smaller subproblems.
- Puzzle Solvers: Solving games like Sudoku or crossword puzzles.
- Combinatorial Problems: Generating all permutations or combinations of a set.
- Decision-making Problems: Such as the knapsack problem, where decisions are made on whether to include items.
Base Case is a pivotal concept in recursive functions, serving as the stopping condition. Without this safeguard, the function can enter an infinite loop, possibly crashing your program.
In mathematical terms, a function is said to operate recursively when:
And it has a defined starting point when
The base case typically addresses the smallest input or the simplest problem state. In the factorial function, the base case is when
Here is the Python code:
def factorial(n):
# Base Case
if n in (0, 1):
return 1
# Recursive Step
return n * factorial(n - 1)- Identify the Simplest Problem: Pinpoint the characteristics of a problem that can be solved directly and quickly without further reduction.
- Establish the Stopping Criterion: Define a condition that, once met, triggers the direct solution without the need for further recursive calls.
- Handle the Base Case Directly: Upon satisfying the stopping condition, solve the problem directly and return the result.
Tip: Explicitly stating the base case at the beginning of the function can enhance code clarity.
Recursion depth refers to the number of times a function calls itself, typically visualized as a call stack.
As functions recursively call themselves, a stack of queued, yet-to-complete recursive function calls forms. When the limit of recursive calls is reached or excessive memory isn't available, you encounter a "stack overflow."
The time and space complexities of an algorithm can be linked to its recursion depth.
-
Best-Case: The algorithm might have constant time complexity, but if the recursion depth reaches
$k$ , then the overall time complexity is$O(k)$ . -
Worst-Case: If the recursion depth is
$n$ , the time complexity is typically$O(n)$ .
- The space complexity is calculated in
$O(1)$ or$O(n)$ terms, depending on whether the stack remains bounded by a small constant or grows with$n$ , respectively.
-
Tail-Call Optimization (TCO): Certain programming languages optimize tail-recursive calls, ensuring that they don't add to the call stack. This effectively converts a recursive function into an iterative one.
-
Explicit Control: In some situations, you can avoid or reduce recursion depth by using loops or memoization.
-
Iterative Alternatives: Algorithms initially implemented using recursion can often be transformed to use loops instead, circumventing the need for stack memory.
Call Stacks provide a strategy for tracking active function calls and managing local variables.
Let's see how the call stack operates in the context of recursive functions and go through an example:
Here is the Python code:
def factorial(n):
if n <= 1:
return 1
return n * factorial(n - 1)
result = factorial(5)
print(result)In the example, result will be 120.
-
Function Call: When
factorialis invoked with5, a new frame is created and pushed onto the stack.factorial(5) -
Base Case Check: Upon each function call, the
Ifcondition checks ifn <= 1. If it is, the top frame is popped from the stack, and the result is returned, terminating the sequence. -
Recursion: If the base case doesn't apply, the function calls itself with a reduced argument. This "recursive" call is pushed onto the stack:
factorial(4)The stack might look like this:
factorial(5) factorial(4) -
Backtracking: After the base case is met, the call stack starts unwinding and calculating results. This process unwinds the call stack, returning the factorial result for each frame in the call sequence.
The call stack for our factorial example will look like this during its lifecycle:
Empty Stack
Push factorial(5)
factorial(5)
Push factorial(4)
factorial(4) -> factorial(5) (top)
Push factorial(3)
factorial(3) -> factorial(4) -> factorial(5) (top)
Push factorial(2)
factorial(2) -> factorial(3) -> factorial(4) -> factorial(5) (top)
Push factorial(1)
factorial(1) -> factorial(2) -> factorial(3) -> factorial(4) -> factorial(5) (top)
Push return 1
return 1 -> factorial(2) -> factorial(3) -> factorial(4) -> factorial(5) (top)
Push return 2
return 1 -> factorial(2) -> factorial(3) -> factorial(4) -> factorial(5) (top)
Push return 6
return 2 -> factorial(3) -> factorial(4) -> factorial(5) (top)
Push return 24
return 6 -> factorial(4) -> factorial(5) (top)
Push return 120
return 24 -> factorial(5) (top)
Pop Final Factorial
Empty Stack
After factorial(1) returns 1, each frame multiplies its return value by the respective n before returning. This results in the final 120 on top of the stack before being returned and popping all the frames from the stack.
7. Are there any safety considerations when determining the Recursion Depth? If yes, provide an example.
When dealing with recursion, excessive recursion depth can lead to stack overflow errors or, in rare cases, security vulnerabilities.
Excessive recursion can lead to stack overflow, a condition where the program runs out of stack space and crashes. Each recursive call contributes to the stack, and if there are too many calls, the stack can't keep up.
Consider the following Python example, which gets increasingly slower as n grows:
def countdown(n):
if n <= 0:
return
else:
countdown(n-1)
countdown(10000) # This will failIn web development, excessively deep recursion can burden the UI.
Let's say you have a webpage where an onClick event triggers a JavaScript function handleClick(). If handleClick() makes recursive calls without an exit condition, the browser might stop responding because each function call hogs a portion of the call stack, potentially impacting the entire UI.
In a multi-user environment, such as a web server handling multiple client requests, insufficient resource allocation for handling recursive calls can lead to resource exhaustion and, in extreme situations, open the door to attacks, like a Denial of Service (DoS).
For example, consider a web server that is designed to execute a recursive algorithm to process client requests. If the server has a strict limit on the maximum recursion depth, an attacker could send crafted requests, exploiting the maximum depth and causing the server to crash, rejecting legitimate requests.
In the given Python example, you can experiment with higher values for n and observe how the program exhausts its resources.
def countdown(n):
if n <= 0:
return
else:
countdown(n-1)
# Try with a very high value for n
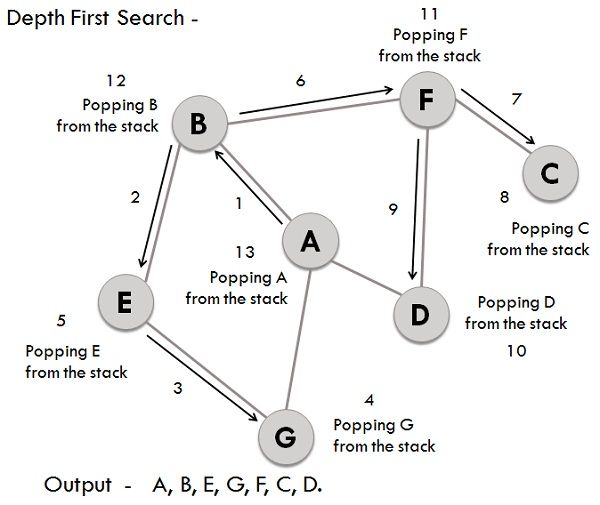
countdown(1000000) # Monitor the memory consumption as an illustrationDepth-First Search (DFS) is a graph traversal algorithm that's simpler and often faster than its breadth-first counterpart (BFS). While it might not explore all vertices, DFS is still fundamental to numerous graph algorithms.
- Initialize: Select a starting vertex, mark it as visited, and put it on a stack.
- Loop: Until the stack is empty, do the following:
- Remove the top vertex from the stack.
- Explore its unvisited neighbors and add them to the stack.
- Finish: When the stack is empty, the algorithm ends, and all reachable vertices are visited.
Here is the Python code:
def dfs(graph, start):
visited = set()
stack = [start]
while stack:
vertex = stack.pop()
if vertex not in visited:
visited.add(vertex)
stack.extend(neighbor for neighbor in graph[vertex] if neighbor not in visited)
return visited
# Example graph
graph = {
'A': {'B', 'G'},
'B': {'A', 'E', 'F'},
'G': {'A'},
'E': {'B', 'G'},
'F': {'B', 'C', 'D'},
'C': {'F'},
'D': {'F'}
}
print(dfs(graph, 'A')) # Output: {'A', 'B', 'C', 'D', 'E', 'F', 'G'}The objective is to write a recursive algorithm that conducts a binary search on an array of
While a recursive solution may not be the most efficient for binary search, as it can lead to stack overflow with long lists, it's essential for practice and understanding of recursion.
-
Base Case: If the array is empty, return
False. -
Recursive Step: Inspect the midpoint. If it matches
$x$ , returnTrue. Otherwise, probe the appropriate half of the array based on the comparison of the midpoint value with$x$ .
-
Time Complexity:
$O(\log n)$ -
Space Complexity:
$O(\log n)$
Here is the Python code:
def binary_search_recursive(arr, low, high, x):
if high >= low:
mid = (high + low) // 2
# If element is present at the middle
if arr[mid] == x:
return True
# Search left subarray
elif arr[mid] > x:
return binary_search_recursive(arr, low, mid - 1, x)
# Search right subarray
else:
return binary_search_recursive(arr, mid + 1, high, x)
else:
# Element is not present in array
return FalseThe Tower of Hanoi puzzle consists of three rods and a number of disks of different sizes, which can slide onto any rod. The puzzle starts with all disks stacked in increasing sizes on the first rod in ascending order, with the smallest on top. The objective is to move the entire stack to the last rod following these rules:
- Only one disk must be moved at a time.
- A disk must never be placed on top of a smaller disk.
The Tower of Hanoi puzzle can be elegantly solved using recursion. By assuming you have a function hanoi to handle moving disks from one peg to another, you can construct the recursion.
- Move
n-1disks from the start peg to the extra peg, using the destination peg as the temporary peg. - Move the remaining largest disk from the start peg to the destination peg.
- Move the
n-1disks from the extra peg to the destination peg, using the start peg as the temporary peg.
-
Time Complexity:
$O(2^n)$ . Although each disk is only moved once, the pattern of recursive calls results in an exponential number of moves. -
Space Complexity:
$O(n)$ due to the function call stack.
Here is the Python code:
def hanoi(start, dest, extra, n):
if n == 1:
# Base case: move the smallest disk
print(f"Move from {start} to {dest}")
return
# Move n-1 disks to the extra peg
hanoi(start, extra, dest, n-1)
# Move the largest disk to the destination peg
print(f"Move from {start} to {dest}")
# Move the n-1 disks from the extra peg to the destination peg
hanoi(extra, dest, start, n-1)
# Test the function with 3 disks
hanoi('A', 'C', 'B', 3)The task is to determine whether a given string,
-
$s = \text{"radar"}$ : Palindrome -
$s = \text{"hello"}$ : Not a palindrome
We can solve this recursively by comparing characters from the start and end of the string.
- Base Case: For strings of length 0 or 1, return true.
- Recursion Step: Compare the first and last characters. If they are equal, check if the substring between them is a palindrome.
-
Time Complexity:
$O(n)$ where$n$ is the string's length. This is due to the$n/2$ comparisons made in each recursive call. -
Space Complexity:
$O(n)$ due to the recursive stack.
Here is the Python code:
def is_palindrome(s):
s = s.lower() # convert to lowercase to handle cases like "Aa"
if len(s) <= 1:
return True
if s[0] != s[-1]:
return False
return is_palindrome(s[1:-1])
# Test the function
print(is_palindrome("radar")) # Output: True
print(is_palindrome("hello")) # Output: FalseThe in-order tree traversal, often referred to as the "left-root-right" traversal, is a classic example of recursion in action. It involves visiting nodes in a binary tree in a specific order.### Traversal Steps
-
Visit the Left Subtree: Recursively traverse the left subtree.
-
Visit the Root Node: The node where traversal starts.
-
Visit the Right Subtree: Recursively traverse the right subtree.
Here is the Python code:
def in_order_traversal(node):
if node:
in_order_traversal(node.left)
print(node.data)
in_order_traversal(node.right)The task is to compute the
Tail recursion offers an optimized approach to compute the Fibonacci series. In this method, the function updates parameters and makes a single recursive call as its last operation, effectively transforming the recursion into a loop.
The function utilizes two accumulators, a and b, to store Fibonacci values and recursively computes the series.
-
Time Complexity:
$O(n)$ -
Space Complexity:
$O(1)$ due to the optimized call stack. It suitable for larger values of$n$ .
Here is the Python code:
def fib_tail(n, a=0, b=1):
if n == 0:
return a
return fib_tail(n - 1, b, a + b)Tail call optimization (TCO) is a compiler feature that promotes efficient memory usage in languages like Erlang, Haskell, and Scheme. It does so by converting certain types of recursive functions, known as "tail-recursive calls," into a looping structure, rather than employing a traditional call stack.
-
Traditional Recursion: Each function call uses stack memory, which can lead to stack overflow if the depth of recursion is too high.
-
Tail Recursion with TCO: The compiler reuses the same stack frame and can, in some cases, eliminate the need for stack memory altogether.
-
What is a Tail Call?: A function call is a tail call if it's the last operation before the current function returns.
-
When Does TCO Occur?: The compiler applies TCO when it recognizes tail calls, ensuring the recursive function doesn't leave any work to be done after the recursive call.
-
Comparing Tail Calls: In non-tail-recursive calls, the returned value and any other operations often require further processing by the calling function, which isn't the case for tail-call-optimized functions.
Here is the Ruby code:
# Non-tail-recursive function
def factorial_non_tail(n)
return 1 if n == 0
n * factorial_non_tail(n - 1)
end
# Tail-recursive function
def factorial_tail(n, accumulator = 1)
return accumulator if n == 0
factorial_tail(n - 1, n * accumulator)
endWhile TCO might not be guaranteed in languages like Java or C++, many modern compilers extend this feature to support both tail-call optimized and general tail-recursive functions.
-
Real-World Example: The Mars Rover Kata demonstrates TCO. A primary advantage is that it helps in managing program state.
-
Safe for Large Inputs: Tail call-optimized functions allow for safe handling of large inputs, which can be especially beneficial in domains like scientific computing or data processing.
-
Discreet Implementation: Shepherd resource usage by keeping the call stack more compact.
-
Functional Programming: It is especially relevant to functional programming styles, where recursive definition is common.
Let's explore the concepts of Head Recursion and Tail Recursion.
- Head Recursion: Like James Bond, it gets "right to the action," leaving the "clean-up" for last.
- Tail Recursion: Follows actions on the "go," much like James Bond racing through an action scene.
Suppose you, as Bond, need to navigate a maze, represented as a sequence of instructions (each with a code name), and perform specific actions:
- Head Recursion: Upon finding an instruction, Bond plans to apply it to the next target in the endless sequence. He first solves the whole maze, recording the actions needed, and then executes the actions in the reverse order.
- Tail Recursion: When Bond first locates an instruction, he adapts it to the current target and then hastens to the next location, repeating this process until he reaches the end of the maze or finds a better course of action.
Bond covertly records his actions as a strategist provides instructions to demonstrate each technique.
Maze Sequence: A -> B -> C -> D
Action Order: Left (A), Left (B), Left (C), Left (D)
James Bond: "I'll analyze the entire sequence initially and follow it step-by-step, but in reverse."
Maze Sequence: A -> B -> C -> D
Action Order: Left (A)
James Bond: "I'll adapt my actions at each point, operating in real-time for the best outcome."
Both Head and Tail Recursion strategies frequently employ recursive functions, which call themselves to process smaller segments of data.
- The head-recursive method affixes its adversarial "action" before the recursive call, leaving the "clean-up" for the resolve phase.
- The tail-recursive function "deal with the mess" before the recursive invocation, ensuring a smoother operation with each iteration.
The Bond agent will navigate the maze as shown:
A -> B -> C -> D
Here is the Python code for the Head Recursion:
def head_recursion(maze_sequence, action_order):
if maze_sequence:
head_recursion(maze_sequence[:-1], action_order) # Recursive call
action_order.append(f"Left {maze_sequence[-1]}") # Action before call
# Initial setup
maze_sequence = ["A", "B", "C", "D"]
actions = []
head_recursion(maze_sequence, actions)
print(actions) # Expected: ["Left A", "Left B", "Left C", "Left D"]The Bond agent navigates the maze as:
Arrives at A, action: "Left A", move to B
Arrives at B, action: "Left B", move to C
Arrives at C, action: "Left C", move to D
Arrives at D, action: "Left D", end of maze
Here is the Python code for Tail Recursion:
def tail_recursion(maze_sequence, action_order):
if maze_sequence:
action_order.append(f"Left {maze_sequence[0]}") # Action before call
tail_recursion(maze_sequence[1:], action_order) # Recursive call
# Initial setup
maze_sequence = ["A", "B", "C", "D"]
actions = []
tail_recursion(maze_sequence, actions)
print(actions) # Expected: ["Left A", "Left B", "Left C", "Left D"]Explore all 53 answers here 👉 Devinterview.io - Recursion Algorithm