PyTorch implementation for the Neuro-Symbolic Sudoku Solver leveraging the power of Neural Logic Machines (NLM). Please note that this is not an officially supported Google product. This project is a direct application of work done as part of original NLM project. We have applied NLM concept to solve more complex (Solving Sudoku) problems. We have also described the internal workings in Medium Blog.
⭐ Star us on GitHub — it helps!
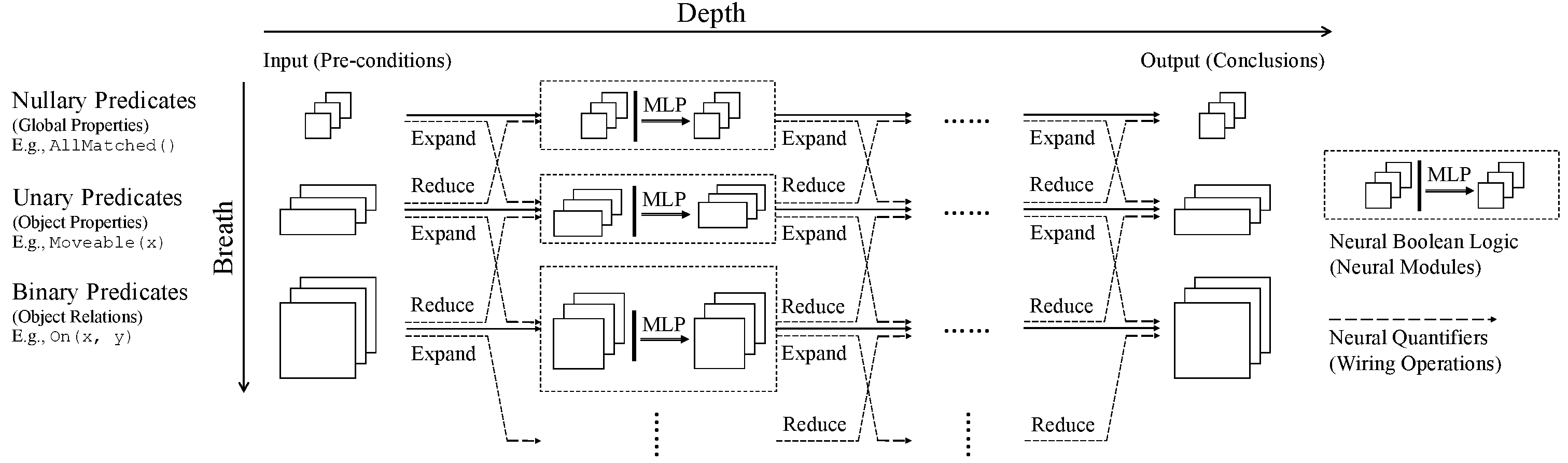
Neural Logic Machine (NLM) is a neural-symbolic architecture for both inductive learning and logic reasoning. NLMs use tensors to represent logic predicates. This is done by grounding the predicate as True or False over a fixed set of objects. Based on the tensor representation, rules are implemented as neural operators that can be applied over the premise tensors and generate conclusion tensors. Learn more about NLM from the paper.
We have used below boolean predicates as inputs to NLM architecture:
isRow(r, num): Does numbernumpresent in rowrinside Sudoku grid?isColumn(c, num): Does numbernumpresent in columncinside Sudoku grid?isSubMat(r, c, num): Does numbernumpresent in 3x3 sub-matrix starting with rowrand columnc.
Note here that isRow and isColumn are binary predicates and isSubMat is ternary predicate. We have stacked the results of isRow and isColumn and inputted as binary predicate.
The core architecture of the model contains deep reinforcement learning leveraging representation power of first order logic predicates.
- Python 3.x
- PyTorch 0.4.0
- Jacinle. We use the version ed90c3a for this repo.
- Other required python packages specified by
requirements.txt. See the Installation.
Clone this repository:
git clone https://github.com/ashutosh1919/neuro-symbolic-sudoku-solver.git --recursive
Install Jacinle included as a submodule. You need to add the bin path to your global PATH environment variable:
export PATH=<path_to_neural_logic_machines>/third_party/Jacinle/bin:$PATH
Create a conda environment for NLM, and install the requirements. This includes the required python packages
from both Jacinle and NLM. Most of the required packages have been included in the built-in anaconda package:
conda create -n nlm anaconda
conda install pytorch torchvision -c pytorch
This repo is extension of original NLM repository. We haven't removed the codebase of problems solved in the base repository but we are only maintaining the Sudoku codebase in this repository.
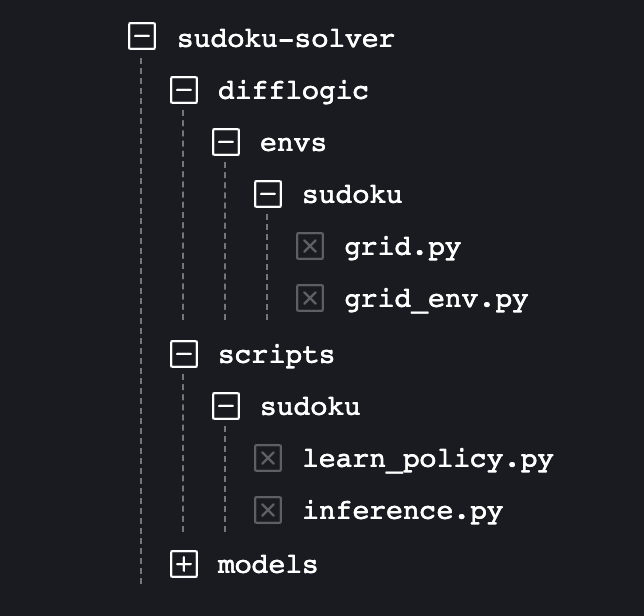
Below is the file structure for the code we have added to original repository to understand things better.
The code in difflogic/envs/sudoku contains information about the environment for reinforcement learning. grid.py selects dataset randomly from 1 Million Sudoku Dataset from Kaggle. grid_env.py creates reinforcement learning environment which can perform actions.
The code in scripts/sudoku/learn_policy.py trains the model whereas scripts/sudoku/inference.py generates prediction from trained model.
We also provide code to download dataset and pre-trained models.
Taking the Sudoku task as an example.
# To download dataset and pre-trained models
$ jac-run scripts/sudoku/download_data_mode.py
# To train the model:
$ jac-run scripts/sudoku/learn_policy.py --task sudoku --dump-dir models
# To infer the model:
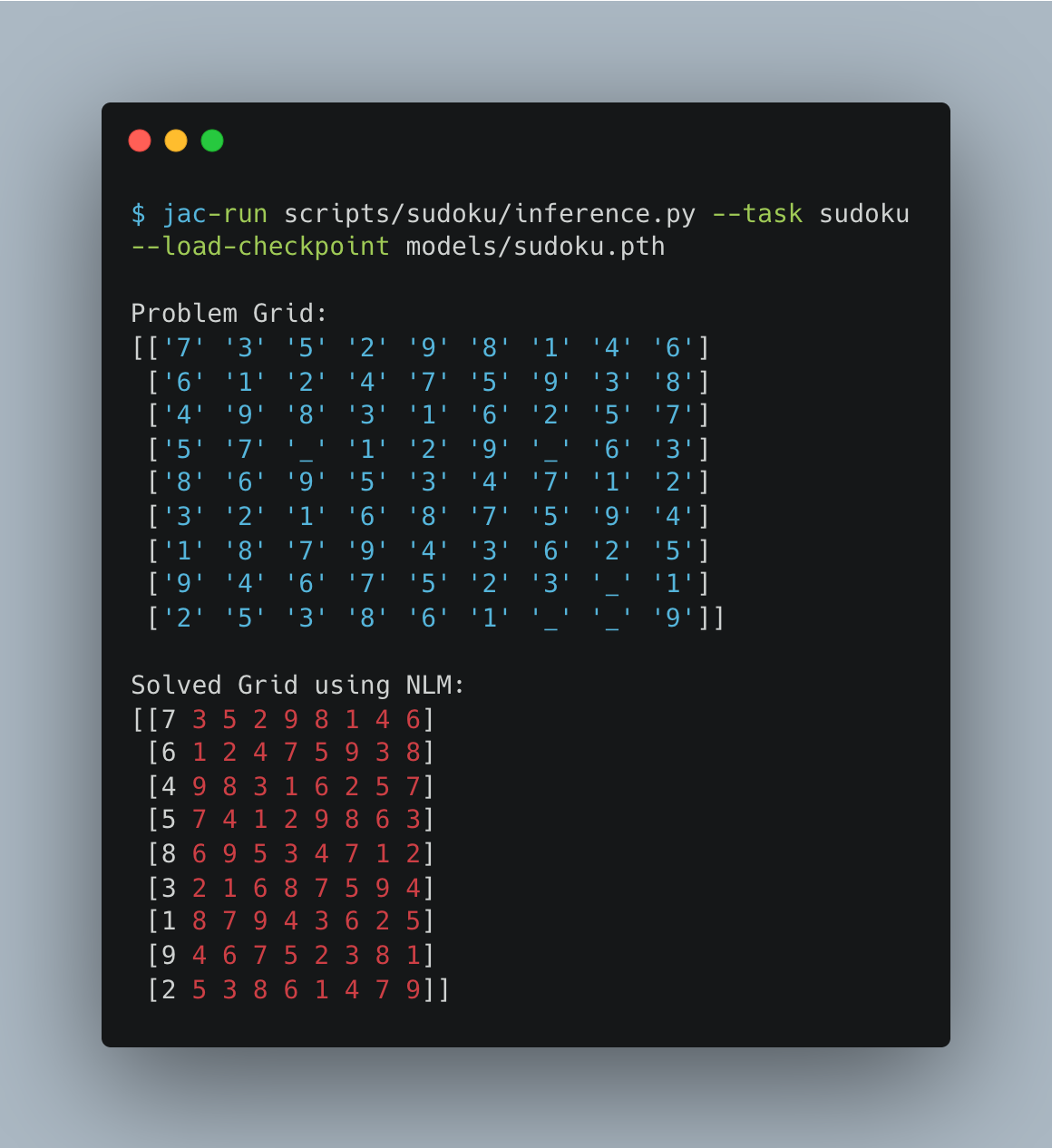
$ jac-run scripts/sudoku/inference.py --task sudoku --load-checkpoint models/sudoku.pthBelow is the sample output that you should get after running inference.py where the program will generate a problem
Sudoku grid and NLM model will solve it.
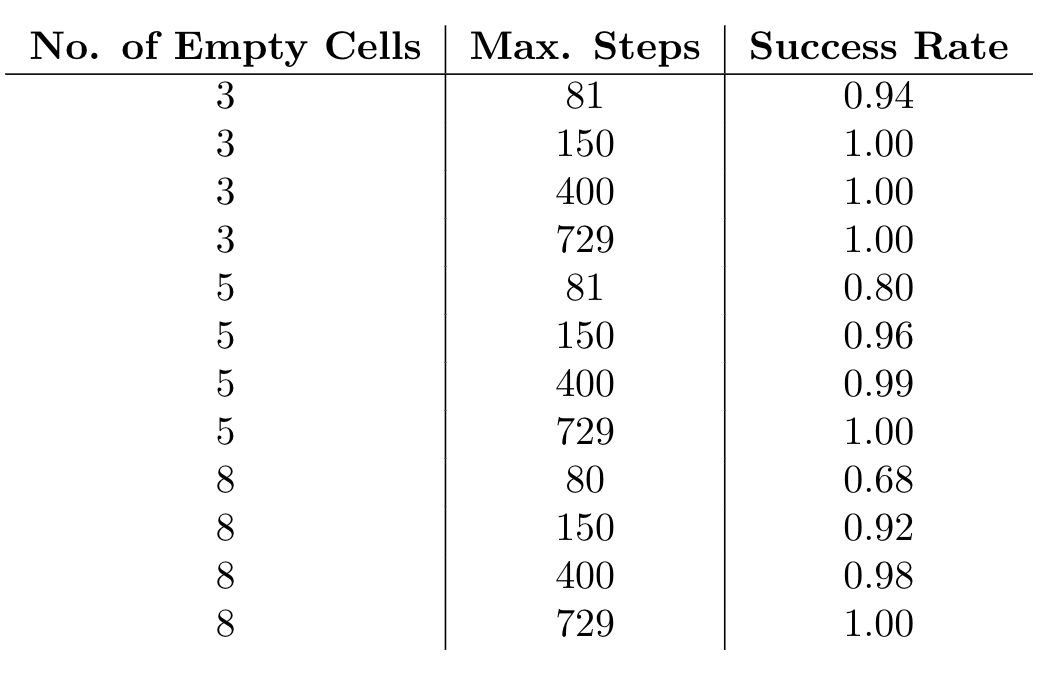
We have trained model with tuning with different parameters and we got below results.
Thanks goes to these wonderful people (emoji key):
Ashutosh Hathidara 💻 🤔 🚧 🎨 📖 💬 🔬 |
Lalit Pandey 💻 📖 🤔 🚧 🎨 💬 🔬 |
This project follows the all-contributors specification. Contributions of any kind welcome!
- Neural Logic Machines Paper and GitHub Repository.
- Reinforce Algorithm & Policy Gradient paper
- 1 Million Sudoku Dataset