- data.C-TSP问题**34个城市的经纬度。
- ga.遗传算法求解TSP问题代码。
对应博文链接:https://blog.csdn.net/zw__chen/article/details/84074000
- 问题描述
行商问题(Travelling Salesman Problem, 简记TSP,亦称货郎担问题):设有n个城市和距离矩阵,其中表示城市i到城市j的距离,i,j=1,2 ... n,则问题是要找出遍访每个城市恰好一次的一条回路并使其路径长度为最短。
- 算法设计
遗传算法是通过模拟生物进化过程来完成优化搜索的,由J. Holland提出的一类借鉴生物界自然选择和自然遗传机制的随机化搜索算法。它起源于达尔文的进化论,是模拟达尔文的遗传选择和自然淘汰的生物进化过程的计算模型。其主要特点是群体搜索策略和群体中个体之间的信息交换,搜索不以梯度信息为基础。“优胜劣汰”这一自然规律的生物进化过程本身是一个自然的、并行发生的、鲁棒的优化过程,生物种群通过生物体的遗传、变异来提高对环境的适应性,从而达到优化的目的。整个遗传算法的过程主要包括了如下步骤:
1)参数的设置:确定个体编码方式,这里即为使用节点编号组成TSP路径。 2)初始随机解的生成:随机生成可行路径,路径中不能有重复节点。 3)选择算子:选择父代的策略。 4)交叉算子:交叉父代并产生新个体,同时需要考虑解决节点冲突。 5)变异算子:对新个体进行变异操作 6)保留策略:精英保留或者父代完全不参与子代。
- 核心伪代码
def initPopulation(self):
"""初始化种群"""
for i in 种群数量
gene = [x for x in 染色体长度]
打乱染色体排序
def cross(self, parent1, parent2):
"""交叉"""
随机坐标 index1
随机坐标index2
获取parent2上index1到index2之间的基因片段
for g in parent1基因:
if 当前位置==index1:
将index1到index2之间的基因片段插入 # 插入基因片段
当前位置+1
if g not in index1到index2之间的基因片段:
将parent1基因插入
当前位置+1
交叉变异次数 + 1
return 新的染色体
def mutation(self, gene):
"""突变"""
随机突变基因位置 index1
随机突变基因位置 index2
染色体index1和index2位置基因互换位置
突变次数 + 1
return 新的染色体
def newChild(self):
"""产生新的后代"""
在种群中获取好的染色体作为parent1
随机交叉概率rate
# 按概率交叉
if rate < 初始化的交叉概率:
# 交叉
在种群中获取好的染色体作parent2
交叉(parent1, parent2)
else:
parent1直接复制给后代
# 按概率突变
随机突变概率rate
if rate < 初始化的突变概率:
突变(gene)
return 新的后代
- 代码运行及测试
相关代码请见:GitHub:https://github.com/zhiweichen12/python-GA-TCP
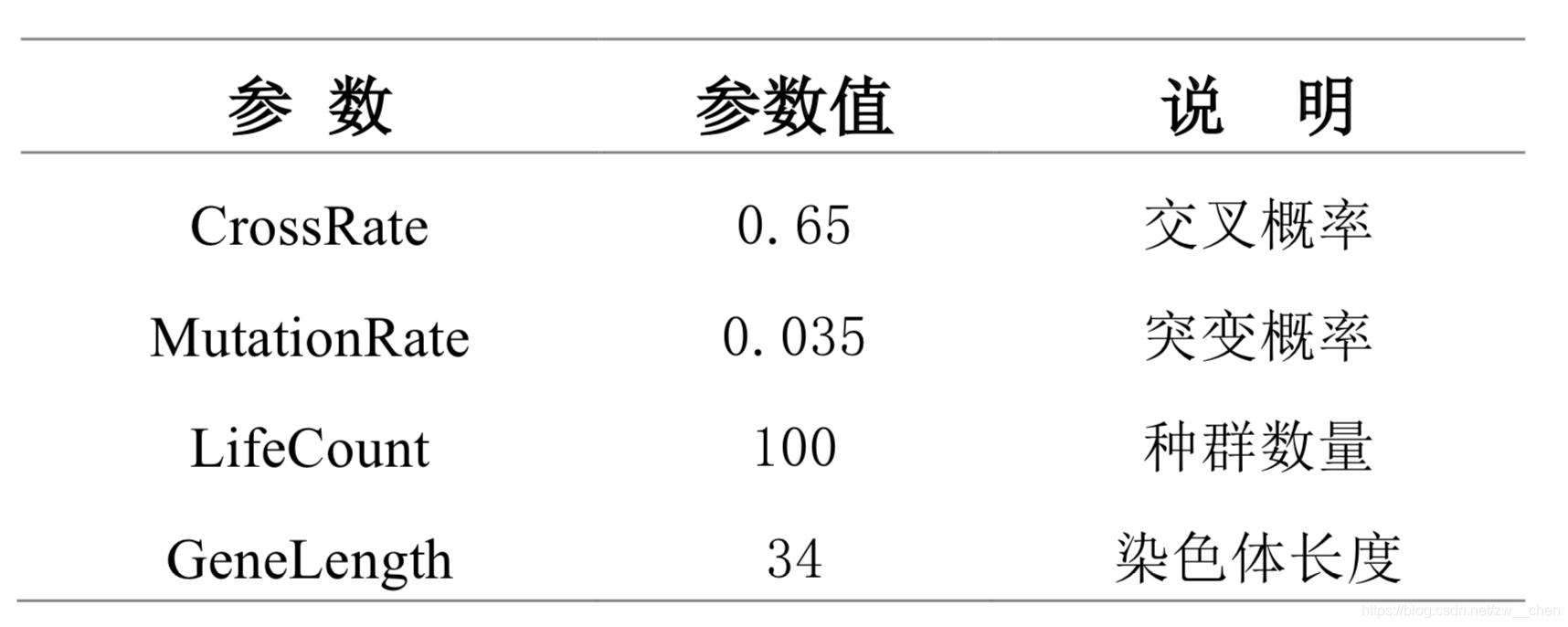
遗传算法因其随机算法的性质,不一定每次都能运行到最优解。同时运行参数的设置对运行结果影响也很大。本实验具体初始化的参数如下表:
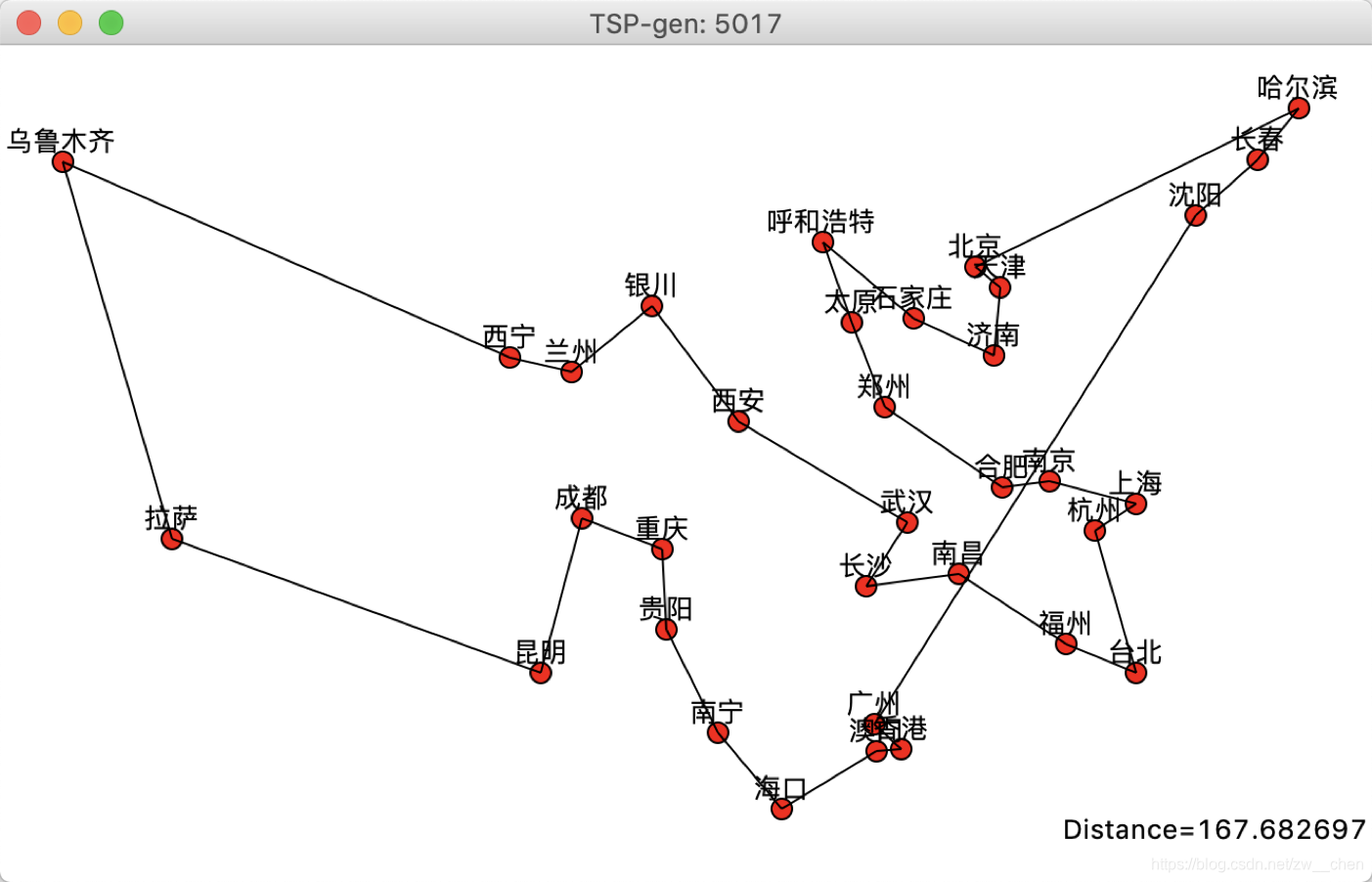
实验数据采用了**34个城市(23个省会、4个直辖市、5个自治区及2个特别行政区)的坐标数据,从经纬度计算欧式距离,作为两两城市间的距离开销。


- 结论
本实验采用的是遗传算法的方式来实现旅行商问题。遗传算法是一种群体性 算法,具有并行性,全局搜索能力极强,局部搜索能力差。参数的选择对算法性 能影响很大,并且需要对问题进行编码。根据前面的实验数据,在处理数据量大 的问题时,需要增大种群大小和增大迭代次数才能使优化值更接近最优解。算法 前期收敛较快,但随着迭代次数的增加,种群陷入局部较优解,需要长时间的迭 代才能继续下降,且越接近最优解越难下降。在核心算子的选择上,本实验采用 了相对特殊的操作方式,在适应性函数和选择操作上,可以做一定的修改,增加 更多的随机因素,而不仅仅依据排序的结果。在交叉操作上,使用到的启发式三 交叉方式产生后两个子代的方式相对朴素,也有改进空间。总体而言,本实验实 现的算法,收敛性能较差,容易陷入局部早熟,这在今后可以调整整体流程,进 一步完善。