Bezier2.m 包含了构建二阶(二次)贝塞尔曲线的源代码,而 Bezier3.m 专用于创建三阶(三次)贝塞尔曲线。BSpline.m 允许通过调整次数(Degree)和控制点的数量(N),生成B样条曲线。设置这些参数后,可以使用鼠标输入 N 个点来可视化结果B样条曲线。
-
$P_i(i=0,1 \ldots n)$ 是控制N边形的$\mathrm{n}+1$ 个顶点。 -
$B_{i, n}(t)$ 是Bernstein基函数,$P_i$ 代表空间中的点,$t \in[0,1]$ ,把$t$ 代进去可以算出一个数, 就是平面或空间的一个点。 - 随着
$t$ 值的变化, 点也在变化,当$t$ 从 0 到 1 , 就得到了 Bezier曲线
公认的是de Boor-Cox递推定义。其内容简单来说是由0次构造 1 次, 由1次构造 2 次, 由 2 次构造 3 次,以此类推。
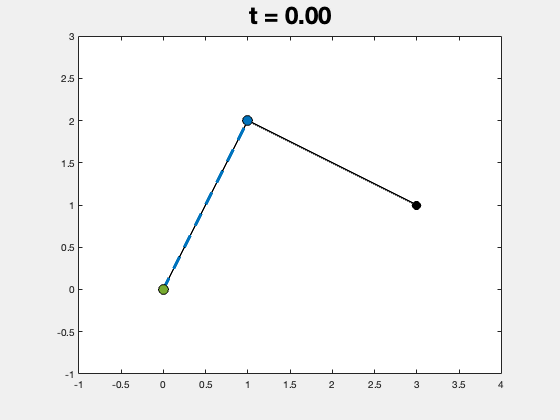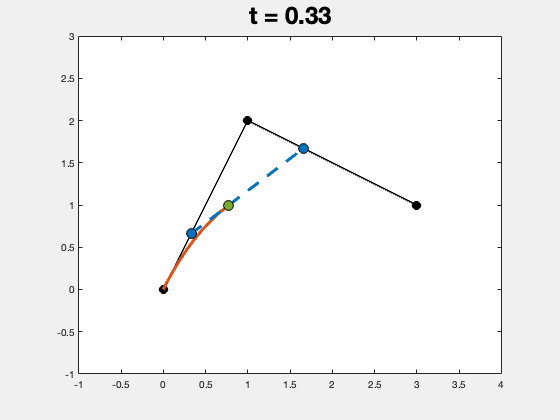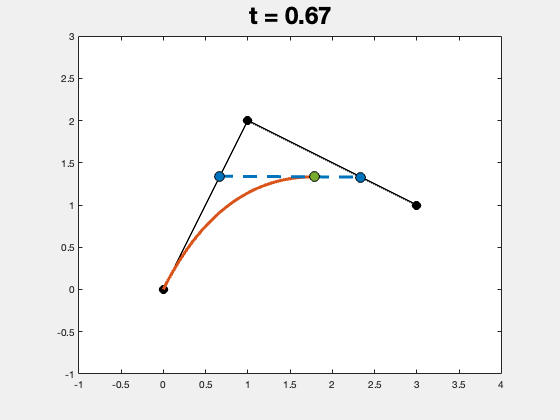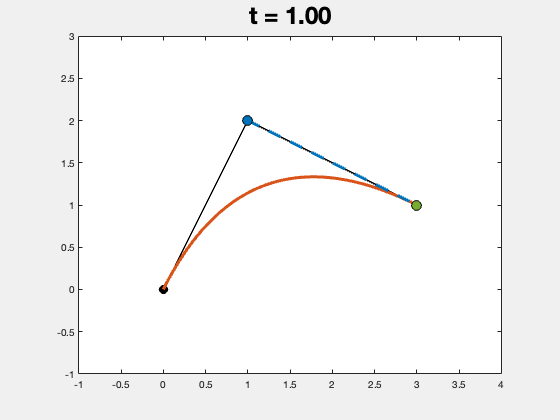
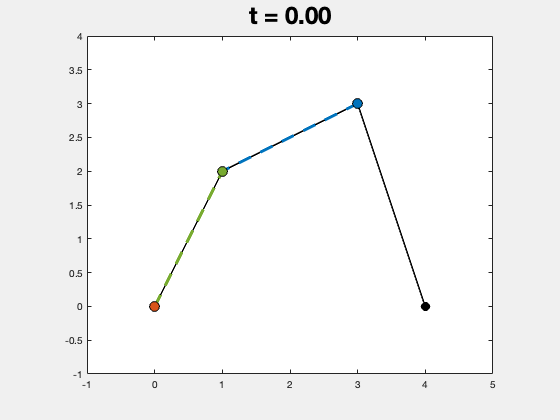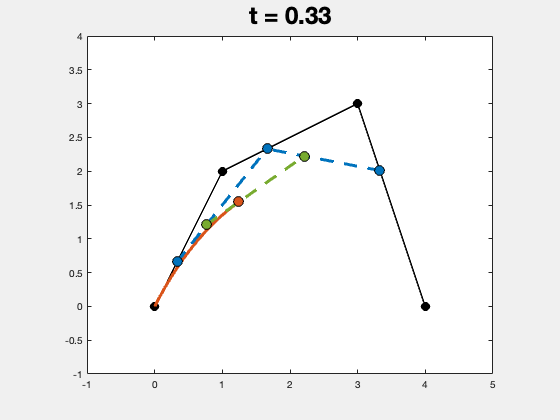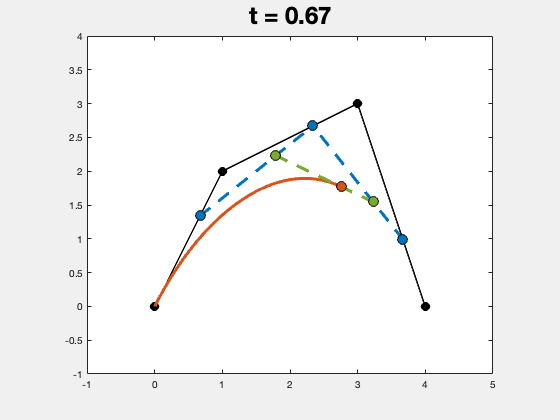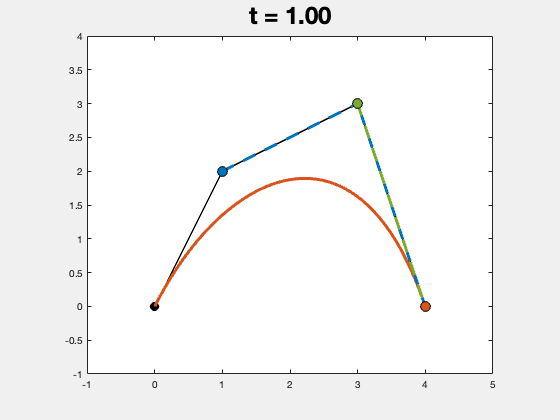
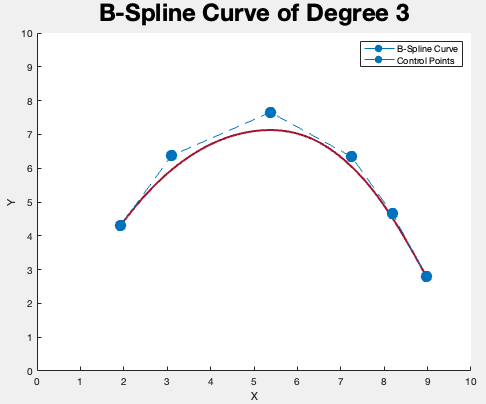
实际的程序运行结果如下图所示,
3次BSpline
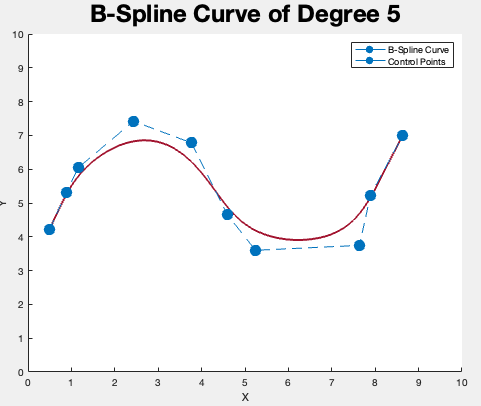
5次BSpline,