/Prolog-Trees

Primary LanguageProlog

A04 - Programming Paradigm: Logic

Student Info

Your name: Edric Yu

Operating system: GalliumOS

Lab computer or your own computer: my own

Did you receive help from your instructor? No

Test Data

tree1(tree(1,tree(2,void,void),tree(3,void,void))).
tree2(tree(4,tree(5,void,void),tree(6,void,void))).
tree3(
        tree(   1,
                tree(   2,
                        tree(5,void,void),
                        tree(   6,
                                tree(7,void,void),
                                void
                        )
                ),
                tree(3,void,void)
        )
).

tree4(tree(42,void,void)).
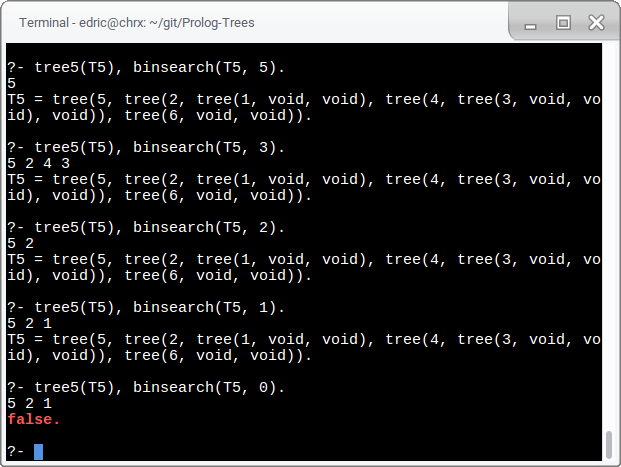
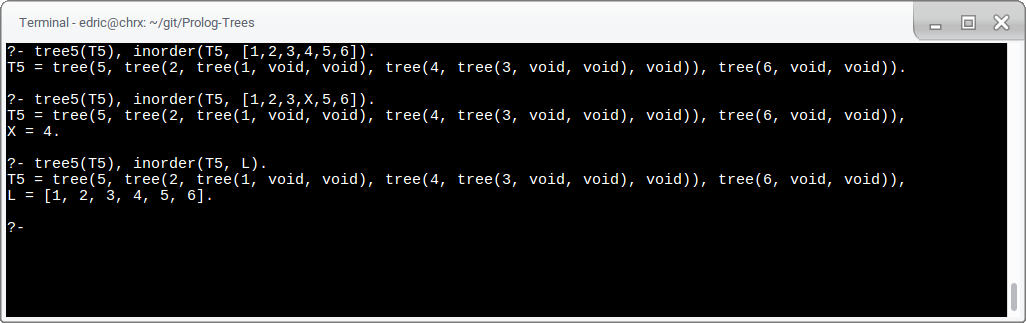
tree5(tree(5,tree(2,tree(1,void,void),tree(4,tree(3,void,void),void)),tree(6,void,void))).
tree6(tree(6,tree(2,tree(1,void,void),tree(4,tree(3,void,void),void)),tree(6,void,void))).
tree7(tree(7,tree(2,tree(1,void,void),tree(4,tree(3,void,void),void)),tree(6,void,void))).
tree8(tree(8,tree(8,tree(8,void,void),tree(8,void,void)),tree(8,void,void))).
tree9(tree(8,tree(8,tree(9,void,void),tree(9,void,void)),tree(9,void,void))).

Rule Implementations

inorder/2

inorder(Tree, List) is true when List is the inorder traversal of Tree.

The first line is interesting to read. It's saying that the statement is true when T5 is equal to that tree. This kind of response happens throughout the rest of the demonstrations.

subtree/2

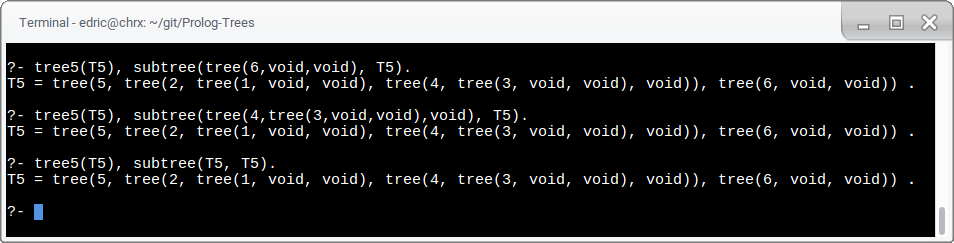
inorder(Subtree, Tree) is true when Subtree is a subtree of Tree.

Notice the "." after each answer. Prolog will keep looking for answers and report false if ";" is used instead

This rule can also be used to generate all subtrees of Tree.

sumtree/2

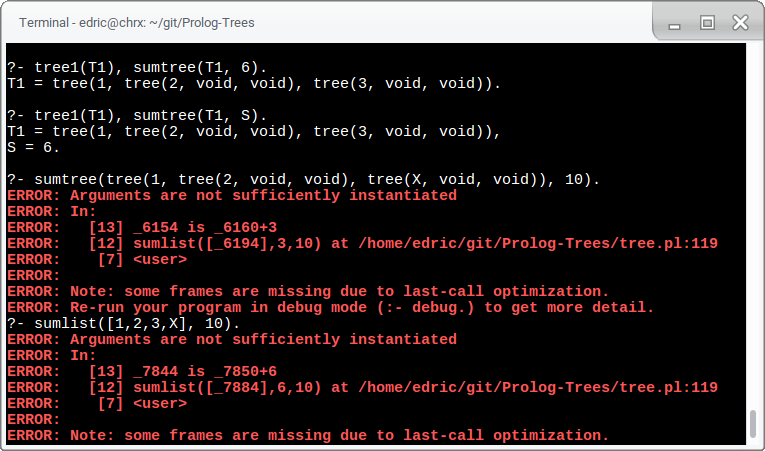
sumtree(Tree, Sum) is true when the elements of Tree sum to Sum. It uses a helper rule sumlist/2 to compute the sum of the list generated from inorder/2.

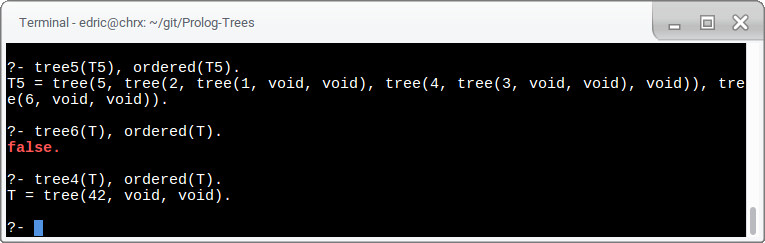
It can compute/verify the sum, but it can't generate a tree based on the sum. sumlist/2 has a similar shortcoming.

ordered/1

ordered(Tree) checks if Tree is ordered like a binary search tree.

search/2

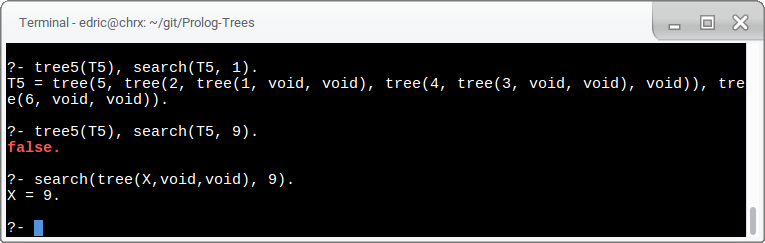
search(Tree, Key) finds if Key is in Tree. It actually invokes the provided tree_member/2.

substitute/4

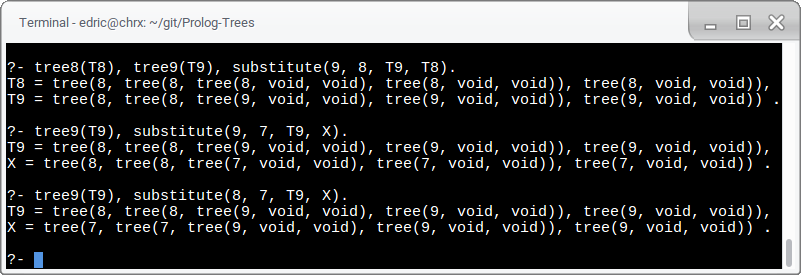
The trickiest rule to implement. substitute(X, Y, TreeX, TreeY) checks if TreeY is the result of replacing all occurrences of X in TreeX with Y.

I noticed that I needed a double implication, which doesn't really exist in prolog except for rule declarations. So I made substituted/4. substituted(XValue, YValue, X, Y) makes sure

XValue = YValue

(x)or

XValue = X and YValue = Y.

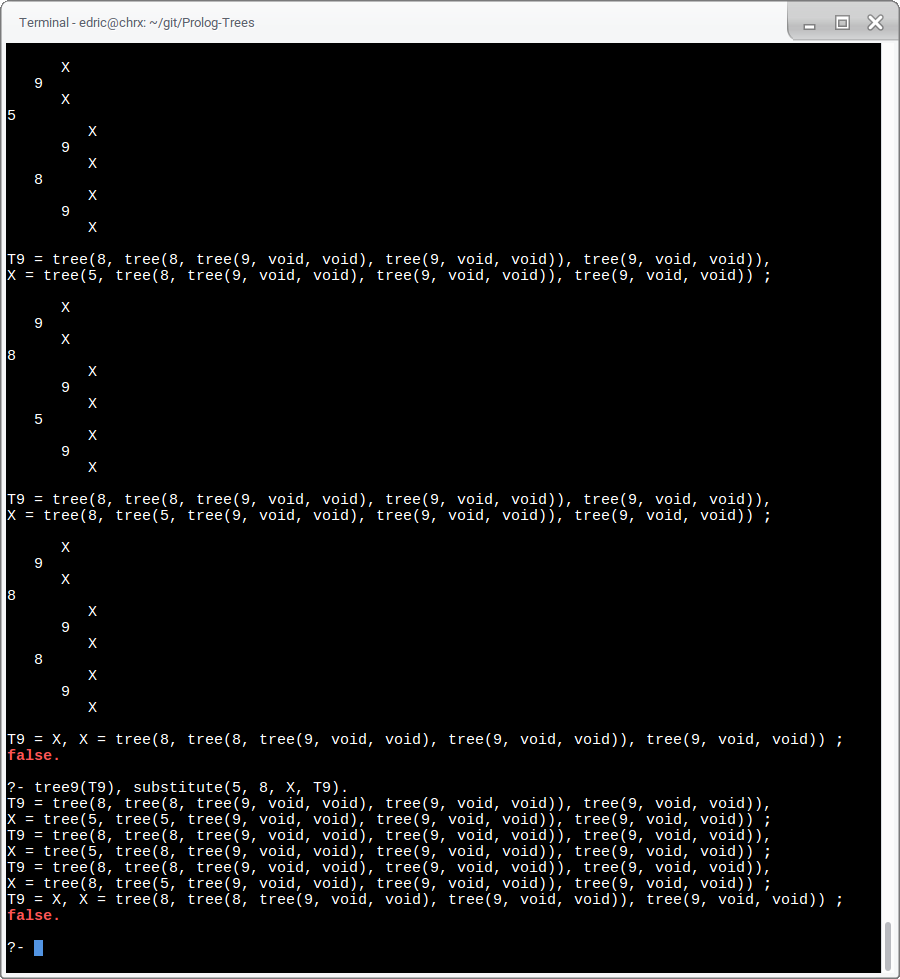
Remember, T8 is a tree of all 8s, and T9 is like T8 but with 9s at each leaf.

substitute/4 can verify or find trees with substitutions made.

substitute/4 can also find the trees that would make the substitute result in the desired tree.

The command was first run with prettyprint. There are 4 answers, and you can see the last 3 from the first run.

Extra credit

prettyprint/1

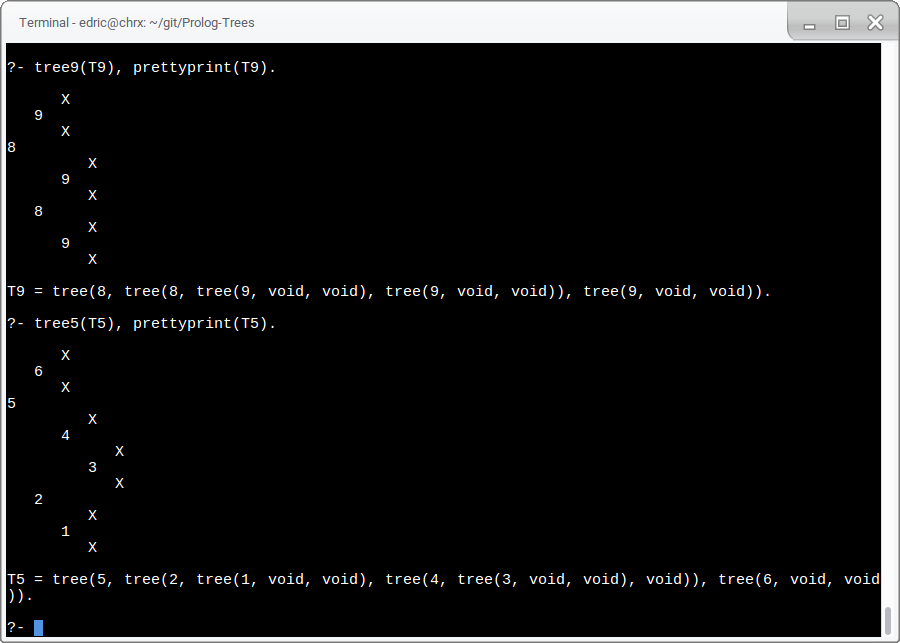
It works! It was never explicitly stated that we could use tab/1, so I made my own tab_over/1.

binsearch/2

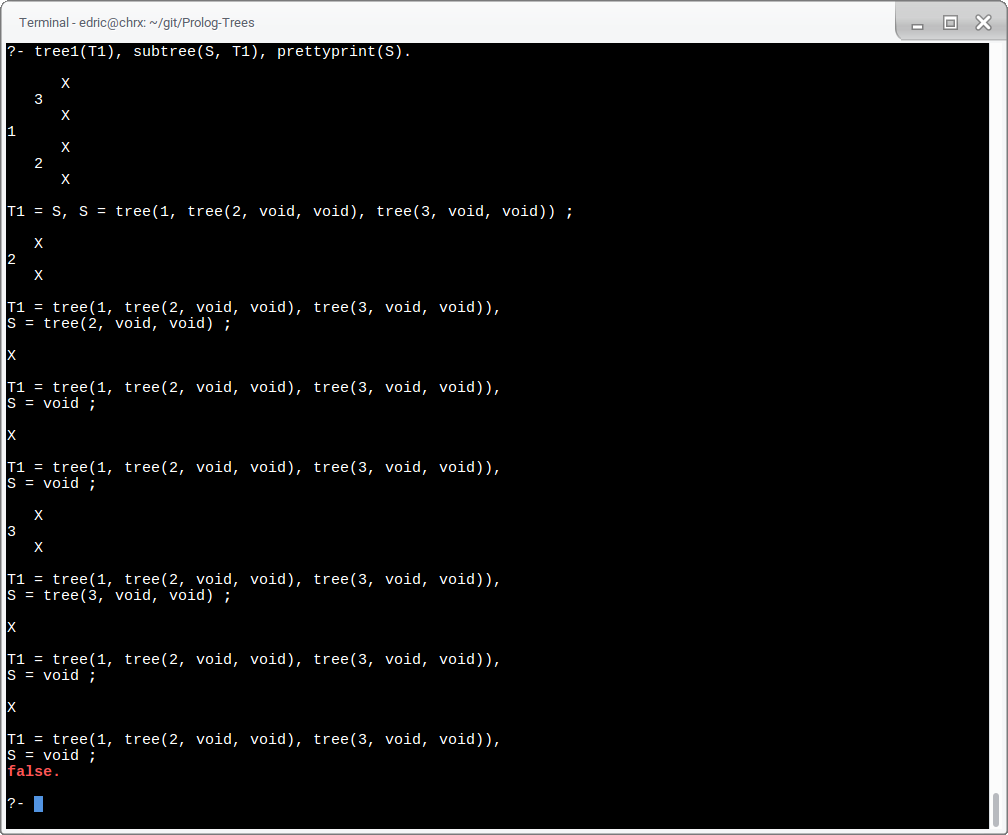
(refer to T5 prettyprint from above)

Assignment Reflection

Hours to complete assignment: ~4

Understanding prolog is pretty cool! I'm not sure if I was supposed to just use tree_member to implement search.

<style class="fallback">body{visibility:hidden;white-space:pre;font-family:monospace}</style><script src="https://casual-effects.com/markdeep/latest/markdeep.min.js"></script><script>window.alreadyProcessedMarkdeep||(document.body.style.visibility="visible");</script>