EiffL/s2fft

Differentiable and accelerated spherical transforms with JAX

Differentiable and accelerated spherical transforms with JAX

S2FFT is a JAX package for computing Fourier transforms on the sphere and rotation group. It leverages autodiff to provide differentiable transforms, which are also deployable on modern hardware accelerators (e.g. GPUs and TPUs).

More specifically, S2FFT provides support for spin spherical harmonic and Wigner transforms (for both real and complex signals), with support for adjoint transformations where needed, and comes with different optimisations (precompute or not) that one may select depending on available resources and desired angular resolution L.

Algorithms ⚡

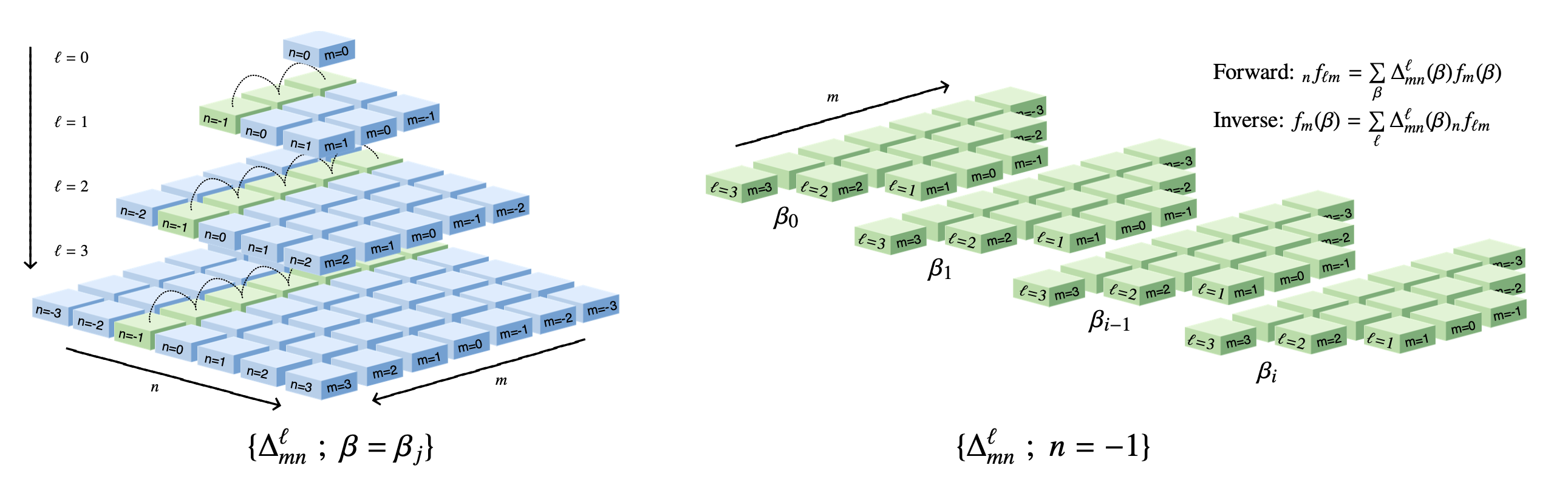
S2FFT leverages new algorithmic structures that can he highly parallelised and distributed, and so map very well onto the architecture of hardware accelerators (i.e. GPUs and TPUs). In particular, these algorithms are based on new Wigner-d recursions that are stable to high angular resolution L. The diagram below illustrates the recursions (for further details see Price & McEwen, in prep.).

Sampling 🌍

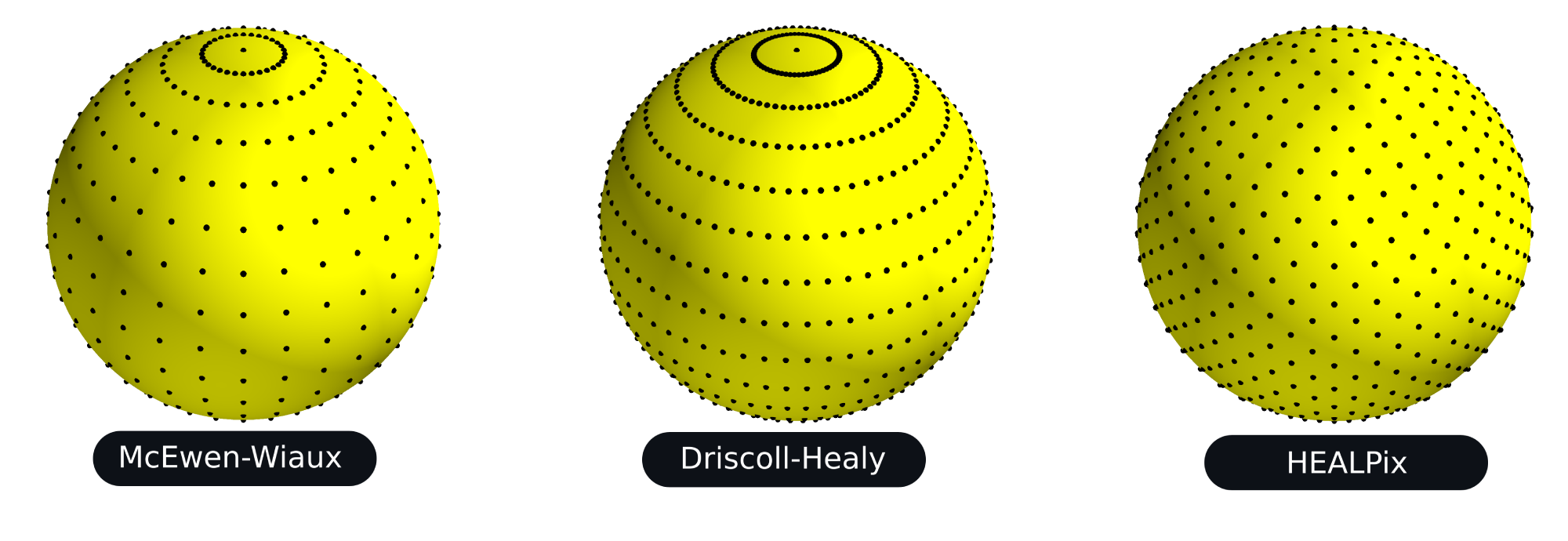
The structure of the algorithms implemented in S2FFT can support any isolattitude sampling scheme. A number of sampling schemes are currently supported.

The equiangular sampling schemes of McEwen & Wiaux (2012) and Driscoll & Healy (1995) are supported, which exhibit associated sampling theorems and so harmonic transforms can be computed to machine precision. Note that the McEwen & Wiaux sampling theorem reduces the Nyquist rate on the sphere by a factor of two compared to the Driscoll & Healy approach, halving the number of spherical samples required.

The popular HEALPix sampling scheme (Gorski et al. 2005) is also supported. The HEALPix sampling does not exhibit a sampling theorem and so the corresponding harmonic transforms do not achieve machine precision but exhibit some error. However, the HEALPix sampling provides pixels of equal areas, which has many practical advantages.

Installation 💻

The Python dependencies for the S2FFT package are listed in the file requirements/requirements-core.txt and will be automatically installed into the active python environment by pip when running

pip install .

from the root directory of the repository. Unit tests can then be executed to ensure the installation was successful by running

pytest tests/         # for pytest
tox -e py38           # for tox

In the very near future one will be able to install S2FFT directly from PyPi by pip install s2fft but this is not yet supported. Note that to run JAX on NVIDIA GPUs you will need to follow the guide outlined by Google.

Usage 🚀

To import and use S2FFT is as simple follows:

For a signal on the sphere # Compute harmonic coefficients flm = s2fft.forward_jax(f, L) # Map back to pixel-space signal f = s2fft.inverse_jax(flm, L)

For a signal on the rotation group # Compute Wigner coefficients flmn = s2fft.wigner.forward_jax(f, L, N) # Map back to pixel-space signal f = s2fft.wigner.inverse_jax(flmn, L, N)

Benchmarking ⏳

We benchmarked the spherical harmonic and Wigner transforms implemented in S2FFT against the C implementations in the SSHT pacakge.

A brief summary is shown in the table below for the recursion (left) and precompute (right) algorithms, with S2FFT running on GPUs (for further details see Price & McEwen, in prep.). Note that our compute time is agnostic to spin number (which is not the case for many other methods that scale linearly with spin).

	Recursive Algorithm			Precompute Algorithm
L	Wall-Time	Speed-up	Error	Wall-Time	Speed-up	Error	Memory
64	3.6 ms	0.88	1.81E-15	52.4 μs	60.5	1.67E-15	4.2 MB
128	7.26 ms	1.80	3.32E-15	162 μs	80.5	3.64E-15	33 MB
256	17.3 ms	6.32	6.66E-15	669 μs	163	6.74E-15	268 MB
512	58.3 ms	11.4	1.43E-14	3.6 ms	184	1.37E-14	2.14 GB
1024	194 ms	32.9	2.69E-14	32.6 ms	195	2.47E-14	17.1 GB
2048	1.44 s	49.7	5.17E-14	N/A	N/A	N/A	N/A
4096	8.48 s	133.9	1.06E-13	N/A	N/A	N/A	N/A
8192	82 s	110.8	2.14E-13	N/A	N/A	N/A	N/A

Contributors 🔨

S2FFT has been developed at UCL, predominantly by Matt Price and Jason McEwen, with support from UCL's Advanced Research Computing (ARC) Centre. The software was funded in part by a UCL-ARC Open Source Software Sustainability grant.

We encourage contributions from any interested developers. A simple first addition could be adding support for more spherical sampling patterns!

Attribution 📚

Should this code be used in any way, we kindly request that the following article is referenced. A BibTeX entry for this reference may look like:

@article{price:s2fft,
   AUTHOR      = "Matthew A. Price and Jason D. McEwen",
   TITLE       = "TBA",
   YEAR        = "2023",
   EPRINT      = "arXiv:0000.00000"
}

You might also like to consider citing our related papers on which this code builds:

@article{mcewen:fssht,
    AUTHOR      = "Jason D. McEwen and Yves Wiaux",
    TITLE       = "A novel sampling theorem on the sphere",
    JOURNAL     = "IEEE Trans. Sig. Proc.",
    YEAR        = "2011",
    VOLUME      = "59",
    NUMBER      = "12",
    PAGES       = "5876--5887",
    EPRINT      = "arXiv:1110.6298",
    DOI         = "10.1109/TSP.2011.2166394"
}

@article{mcewen:so3,
    AUTHOR      = "Jason D. McEwen and Martin B{\"u}ttner and Boris ~Leistedt and Hiranya V. Peiris and Yves Wiaux",
    TITLE       = "A novel sampling theorem on the rotation group",
    JOURNAL     = "IEEE Sig. Proc. Let.",
    YEAR        = "2015",
    VOLUME      = "22",
    NUMBER      = "12",
    PAGES       = "2425--2429",
    EPRINT      = "arXiv:1508.03101",
    DOI         = "10.1109/LSP.2015.2490676"
}

License 📝

We provide this code under an MIT open-source licence with the hope that it will be of use to a wider community.

Copyright 2023 Matthew Price, Jason McEwen and contributors.

S2FFT is free software made available under the MIT License. For details see the LICENSE file.