XPKeygen

A Windows XP / Windows Server 2003 VLK key generator. This tool allows you to generate valid Windows XP keys based on the Raw Product Key, which can be random. The Raw Product Key (RPK) is supplied in form of 9 digits XXX-YYYYYY and is only necessary to generate a Windows XP Key.

Download

Head over to the Releases tab and download the latest version from there.

The problem

In general, the only thing that separates us from generating valid Windows XP keys for EVERY EDITION and EVERY BUILD is the lack of respective private keys generated from their public counterparts inside pidgen.dll. There's no code for the elliptic curve discrete logarithm function widely available online, there's only vague information on how to do it.

As time went on, the problem has been partially solved.

The BINK resource was not encoded in any way and the data was just sequentially written to the resource. sk00ter also fully explained the BINK format on the MDL forums. Utilizing prior community knowledge on the subject, I wrote a BINK Reader in Python 3. The file is public in this repository, click here to view the source code.

The discrete logarithm solution is the most unexplored area of research as of May 28th, 2023. However, my friend nephacks did find that elusive tool to solve that difficult problem in the darkest corners of the internet. It's called ECDLP (Elliptic Curve Discrete Logarithm Problem) Solver by Mr. HAANDI. Since it was extremely frustrating to find online, I did reupload it on my website. You can download the tool here.

The ReadMe file that comes with the version 0.2a of the solver is good enough by itself, so anyone with a brain will be able to set that tool up. However, it's not open-source, so integrating it into my keygen is proven impossible.

In the ideal scenario, the keygen would ask you for a BINK-resource extracted from pidgen.dll, which it would then unpack into the following segments:

Public key (pubX; pubY)
Generator (genX; genY)
Base point (a; b)
Point count p

Knowing these segments, the keygen would bruteforce the geneator order genOrder using Schoof's algorithm followed by the private key privateKey, leveraging the calculated genOrder to use the most optimal Pollard's Rho algorithm. There's no doubt we can crack any private key in a matter of 20 minutes using modern computational power, provided we have the working algorithm.

Once the keygen finishes bruteforcing the correct private key, the task boils down to actually generating a key, which this keygen does. To give you a better perspective, I can provide you with the flow of the ideal keygen. Crossed out is what my keygen implements:

~~BINK resource extraction~~
Bruteforce Elliptic Curve discrete logarithm solution (genOrder, privateKey)
~~Product Key processing mechanism~~
~~Windows XP key generation~~
~~Windows XP key validation~~
~~Windows Server 2003 key generation~~

Principle of operation

We need to use a random Raw Product Key as a base to generate a Product ID in a form of AAAAA-BBB-CCCCCCS-DDEEE.

Product ID

Digits	Meaning
AAAAA	OS Family constant
BBB	Channel ID
CCCCCC	Sequence Number
S	Check digit
DD	Public key index
EEE	Random 3-digit number

The OS Family constant AAAAA is different for each series of Windows XP. For example, it is 76487 for SP3.

The BBB and CCCCCC sections essentially encode the Raw Product Key. For example, if the first section is equal to XXX and the second section is equal to YYYYYY, the Raw Product Key will be encoded as XXX-YYYYYY.

The check digit S is picked so that the sum of all C digits with it added makes a number divisible by 7.

The public key index DD lets us know which public key was used to successfully verify the authenticity of our Product Key. For example, it's 22 for Professional keys and 23 for VLK keys.

A random number EEE is used to generate a different Installation ID each time.

Product Key

The Product Key itself (not to confuse with the RPK) is in form FFFFF-GGGGG-HHHHH-JJJJJ-KKKKK, encoded in Base-24 with the alphabet BCDFGHJKMPQRTVWXY2346789 to exclude any characters that can be easily confused, like I and 1 or O and 0.

As per the alphabet capacity formula, the key can at most contain 114 bits of information. $$N = \log_2(24^{25}) \approx 114$$

Based on that calculation, we unpack the 114-bit Product Key into 4 ordered segments:

Segment	Capacity	Data
Upgrade	1 bit	Upgrade version flag
Serial	30 bits	Raw Product Key (RPK)
Hash	28 bits	RPK hash
Signature	55 bits	Elliptic Curve signature for the RPK hash

For simplicity' sake, we'll combine Upgrade and Serial segments into a single segment called Data. By that logic we'll be able to extract the RPK by shifting Data right and pack it back by shifting bits left, because most a priori valid product keys I've checked had the Upgrade bit set to 1.

Microsoft redid their Product Key format with Windows Server 2003 to include a backend server authentication key, which was an actually secure approach to license validation, as no one could ever make a guess on which validation algorithm they had employed on their private server. Besides adding the online validation mechanism, they also cranked up the overall arithmetic from 384 to 512 bits, and the signature scalar to 62 bits of information.

Segment	Capacity	Data
Upgrade	1 bit	Upgrade version flag
Channel ID	10 bits	The `BBB` part of the RPK
Hash	31 bits	RPK hash
Signature	62 bits	Elliptic Curve signature for the RPK hash
Auth Key	10 bits	Backend authentication value

However, if we generated a key without the online activation in mind, we still could generate valid keys that would let us through the setup of the operating system. And that's exactly what the code does - it generates a random 10-bit authentication key. Nowadays it doesn't matter at all, as activation servers are down and Server 2003 is considered abandonware, the same way this entire project shouldn't be considered piracy.

Elliptic Curves

Elliptic Curve Cryptography (ECC) is a type of public-key cryptographic system. This class of systems relies on challenging "one-way" math problems - easy to compute one way and intractable to solve the "other" way. Sometimes these are called "trapdoor" functions - easy to fall into, complicated to escape.^[5]

ECC relies on solving equations of the form $$y^2 = x^3 + ax + b$$

In general, there are 2 special cases for the Elliptic Curve leveraged in cryptography - F_2m and F_p. They differ only slightly. Both curves are defined over the finite field, F_p uses a prime parameter that's larger than 3, F_2m assumes $p = 2m$. Microsoft used the latter in their algorithm.

An elliptic curve over the finite field F_p consists of:

a set of integer coordinates ${x, y}$, such that $0 \le x, y < p$;
a set of points $y^2 = x^3 + ax + b \mod p$.

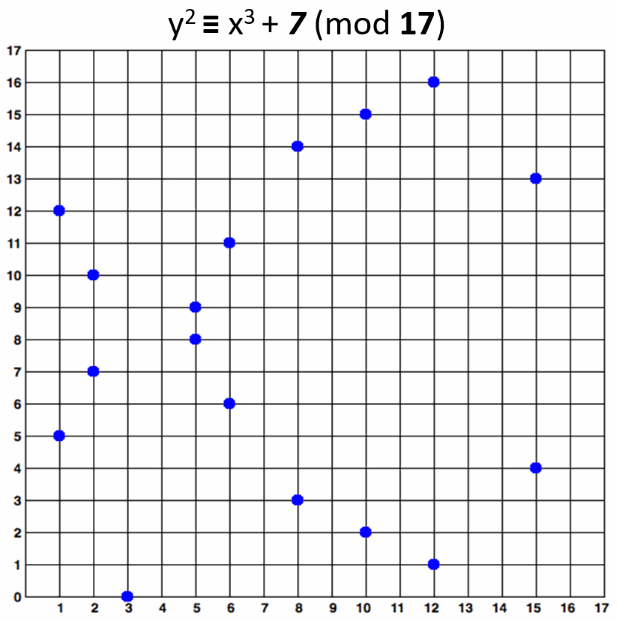
An elliptic curve over F₁₇ would look like this:

The curve consists of the blue points in above image. In practice the "elliptic curves" used in cryptography are "sets of points in a square matrix".

The above curve is "educational". It provides very small key length (4-5 bits). In real world situations developers typically use curves of 256-bits or more.

BINK resource

Since it is a public-key cryptographic system, Microsoft had to share the public key with their Windows XP release to check entered product keys against. It is stored within pidgen.dll in a form of a BINK resource. The first set of BINK data is there to validate retail keys, the second is for the OEM keys respectively.

The structure of the BINK resource for Windows 98 and Windows XP is as follows:

Offset	Value
`0x0000`	BINK ID
`0x0004`	Size of BINKEY structure in bytes (always `0x16C` in practice)
`0x0008`	Header length (always `7` in practice)
`0x000C`	Checksum
`0x0010`	Number-encoded date - BINKEY version (always `19980206` in practice)
`0x0014`	ECC curve order size (always `12` in practice)
`0x0018`	Hash length (always `28` in practice)
`0x001C`	Signature length (always `55` in practice)
`0x0020`	Finite Field Order `p`
`0x005C`	Curve Parameter `a`
`0x0098`	Curve Parameter `b`
`0x00D4`	Base Point x-coordinate `Gx`
`0x0110`	Base Point y-coordinate `Gy`
`0x014C`	Public Key x-coordinate `Kx`
`0x0188`	Public Key y-coordinate `Ky`

Each segment is marked with a different color, the BINK header values are the same.

Windows Server 2003 and Windows XP x64 implement it differently:

Offset	Value
`0x0000`	BINK ID
`0x0004`	Size of BINKEY structure in bytes
`0x0008`	Header length (always `9` in practice)
`0x000C`	Checksum
`0x0010`	Number-encoded date - BINKEY version (always `20020420` in practice)
`0x0014`	ECC curve order size (always `16` in practice)
`0x0018`	Hash length (always `31` in practice)
`0x001C`	Signature length (always `62` in practice)
`0x0020`	Backend authentication value length (always `12` in practice)
`0x0024`	Product ID length (always `20` in practice)
`0x0028`	Finite Field Order `p`
`0x0068`	Curve Parameter `a`
`0x00A8`	Curve Parameter `b`
`0x00E8`	Base Point x-coordinate `Gx`
`0x0128`	Base Point y-coordinate `Gy`
`0x0168`	Public Key x-coordinate `Kx`
`0x01A8`	Public Key y-coordinate `Ky`

And here are my structure prototypes made for the BINK Reader in C:

typedef struct _EC_BYTE_POINT {
    CHAR x[256];    // x-coordinate of the point on the elliptic curve.
    CHAR y[256];    // y-coordinate of the point on the elliptic curve.
} EC_BYTE_POINT;

typedef struct _BINKHDR {
    // BINK version - not stored in the resource.
    ULONG32 dwVersion;

    // Original BINK header.
    ULONG32 dwID;
    ULONG32 dwSize;
    ULONG32 dwHeaderLength;
    ULONG32 dwChecksum;
    ULONG32 dwDate;
    ULONG32 dwKeySizeInDWORDs;
    ULONG32 dwHashLength;
    ULONG32 dwSignatureLength;
    
    // Extended BINK header. (Windows Server 2003+)
    ULONG32 dwAuthCodeLength;
    ULONG32 dwProductIDLength;
} BINKHDR;

typedef struct _BINKDATA {
    CHAR p[256];        // Finite Field order p.
    CHAR a[256];        // Elliptic Curve parameter a.
    CHAR b[256];        // Elliptic Curve parameter b.

    EC_BYTE_POINT G;    // Base point (Generator) G.
    EC_BYTE_POINT K;    // Public key K.
} BINKDATA;

typedef struct _BINKEY {
    BINKHDR  header;
    BINKDATA data;
} BINKEY;

In case you want to explore further, the source code of pidgen.dll and all its functions is available within this repository, in the "pidgen" folder.

Reversing the private key

If we want to generate valid product keys for Windows XP, we must compute the corresponding private key using the public key supplied with pidgen.dll, which means we have to reverse-solve the one-way ECC task.

Judging by the key located in BINK, the curve order is 384 bits long in Windows XP and 512 bits long in Server 2003 / XP x64 respectively. The computation difficulty using the most efficient Pollard's Rho algorithm with asymptotic complexity $O(\sqrt{n})$ would be at least $O(2^{168})$ for Windows XP, and $O(2^{256})$ for Windows Server 2003, but lucky for us, Microsoft limited the value of the signature to 55 bits in Windows XP and 62 bits in Windows Server 2003 in order to reduce the amount of matching product keys, reducing the difficulty to a far more manageable $O(2^{28})$ / $O(2^{31})$.

As mentioned before, there's only one public tool that satisfies our current needs, which is the ECDLP solver by Mr. HAANDI.

To compute the private key, we will need to supply the tool with the public ECC values located in the BINK resource, as well as the order genOrder of the base point G(Gx; Gy). The order of the base point can be computed using SageMath.

Here's the basic algorithm I used to reverse the Windows 98 private key:

Compute the order of the base point using SageMath. In SageMath, execute the following commands:
1. E = EllipticCurve(GF(p), [0, 0, 0, a, b]), where p, a and b are decimally represented elliptic curve parameters from the BINK resource.
2. G = E(Gx, Gy), where Gx and Gy are decimally represented base point coordinates from the BINK resource.
3. K = E(Kx, Ky), where Kx and Ky are decimally represented public key coordinates from the BINK resource.
4. n = G.order(), n will be the computed order of the base point. It may take some time to compute, even on the newest builds.
5. Factor the order using factor(n). Microsoft used prime numbers for the point orders, so if it returns the number itself, it's completely normal.
6. Save the resulting factors of the order somewhere.
7. -K will give you the inverse of the public key in a projective plane with coordinates (x : y : z). Save the y coordinate somewhere, it is required to generate a correct private key.
Compute the private key using ECDLP Solver v0.2a.
1. The tool comes with a template job job_template.txt and a ReadMe file. It's necessary to understand how the tool works to use it.
2. Insert all public elliptic curve values from the BINK resource, except the Ky coordinate. To generate a correct private key, you must use the inverse coordinate -Ky you have calculated in SageMath earlier.
3. Insert the factors of the base point order n and specify the factor count. It will very likely be 1, as Microsoft mainly uses primes for their generator orders.
4. Run the tool <arch> ECDLP Solver.exe <job_name>.txt and wait until it calculates the private key k = %d for you.

Here's an example of the Windows XP job job_xp.txt that yields the correct private key for the ECDLP Solver.

GF := GF(22604814143135632990679956684344311209819952803216271952472204855524756275151440456421260165232069708317717961315241);
E := EllipticCurve([GF|1,0]);
G := E![10910744922206512781156913169071750153028386884676208947062808346072531411270489432930252839559606812441712224597826,19170993669917204517491618000619818679152109690172641868349612889930480365274675096509477191800826190959228181870174];
K := E![14399230353963643339712940015954061581064239835926823517419716769613937039346822269422480779920783799484349086780408,17120082747148185997450361756610881166187863099877353630300913555824935802439591336620545428308962346299700128114607];
/*
FactorCount:=1;
61760995553426173
*/

And the ECDLP Solver output for it:

Important note:

Be wary that I could not generate a correct Windows XP x64 key using the private key I've reversed, even using the Ky coordinate instead of usual -Ky. For some reason, I also failed to calculate the Windows Server 2003 base point order using SageMath. I gave it 12 hours to compute on my i7-12700K, but it was still stuck calculating.

Validating / generating product keys

The rest of the job is done within the code of this keygen.

Known issues

~~Some keys aren't valid, but it's generally a less common occurrence. About 2 in 3 of the keys should work.~~
Fixed in v1.2. Prior versions generated a valid key with an exact chance of 0x40000/0x62A32, which resulted in exactly 0.64884, or about 65%. My "2 in 3" estimate was inconceivably accurate.
Tested on multiple Windows XP setups. Works on Professional x86, all service packs. Other Windows editions may not work. x64 DOES NOT WORK.
~~Server 2003 key generation not included yet.~~
Fixed in v2.2.
Some Windows XP VLK keys tend to be "worse" than others. Some of them may trigger a broken WPA with an empty Installation ID after install. You have the best chances generating "better" keys with the BBB section set to 640 and the CCCCCC section not zero.
Windows Server 2003 key generation is broken. I'm not sure where to even start there. The keys don't appear to be valid anywhere, but the algorithm is well-documented. The implementation in my case generates about 1 in 3 "valid" keys.
Fixed in v2.3*.

Literature

I will add more decent reads into the bibliography in later releases.

Understanding basics of Windows XP Activation:

Understanding Elliptic Curve Cryptography:

Public discussions:

Contributing / Usage

If you're going to showcase or fork this software, please credit Endermanch, z22 and MSKey.
Feel free to modify it to your liking, as long as you keep it open-source. Licensed under GNU General Public License v3.0.

Any contributions or questions welcome.

EricChen01/XPKeygen