An implementation of Neural Fictitous Self-Play [1] in the PokerRL framework.
This codebase is designed for:
- Researchers to compare new methods to the NFSP baseline.
- Anyone wanting to learn about Deep RL in imperfect information games.
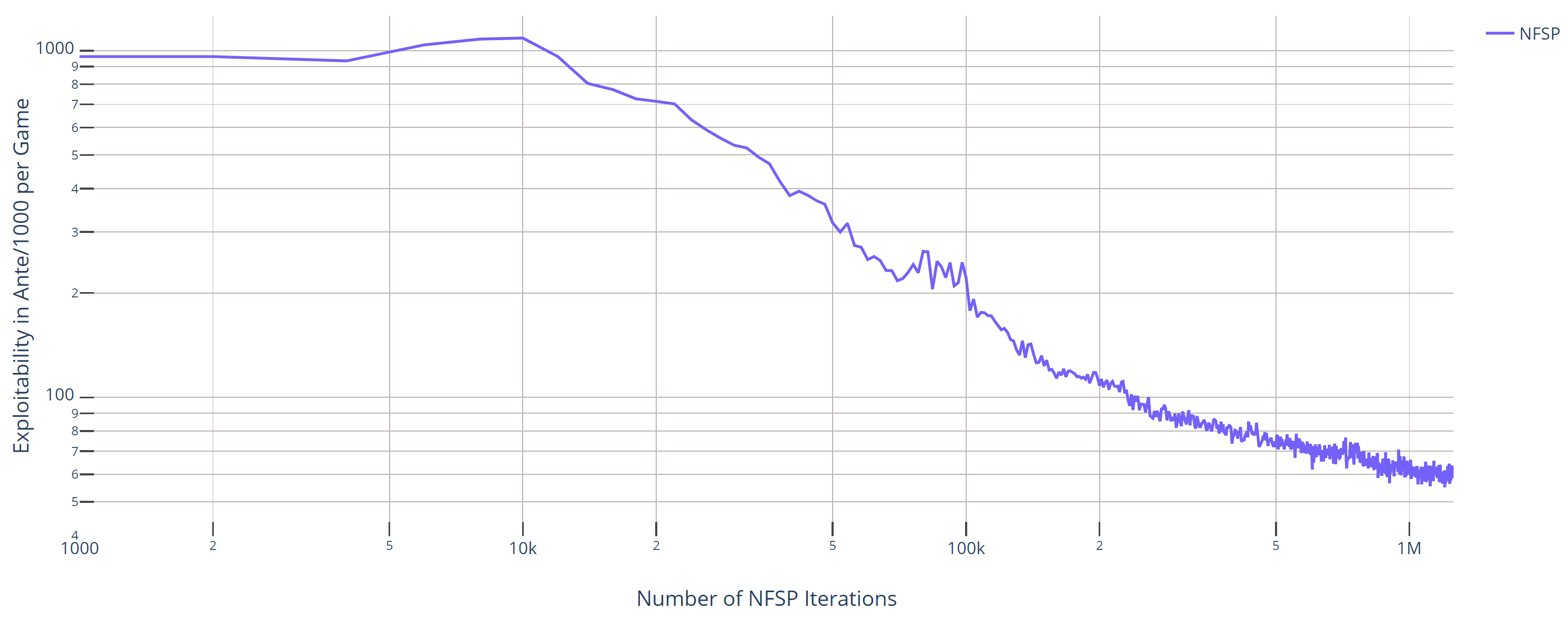
The run-script NFSP/example_paper.py launches NFSP in Leduc Hold'em with the same hyperparameters
(but using 3-layer networks) as the original paper [1]. In the run shown, the
100 mA/g (= 0.1A/g from the paper) line is crossed after 230k iterations (4:24hrs) and
the 60 mA/g line after 850k iterations (19hrs). We trained on a single m5.xlarge instance.
To reproduce, simply run NFSP/example_paper.py.
First, please install Docker and download the PyCrayon container. For dependency management I recommend Miniconda. To install the dependencies, simply activate your conda environment and then run
conda install pytorch=0.4.1 -c pytorch -y
pip install PokerRL
Before starting NFSP, please spin up the log server by
docker run -d -p 8888:8888 -p 8889:8889 --name crayon alband/crayon
docker start crayon
You can now view logs at localhost:8888 in your browser. To run NFSP with custom hyperparameters in any Poker game
supported by PokerRL, build a script similar to NFSP/example_paper.py. Run-scripts define the hyperparameters, the game
to be played, and the evaluation metrics. Here is a very minimalistic example:
from TrainingProfile import TrainingProfile
from workers.driver.Driver import Driver
from PokerRL import BigLeduc # or any other game
if __name__ == '__main__':
ctrl = Driver(
t_prof=TrainingProfile(
name="NFSP_TEST",
game_cls=BigLeduc, # -- The game to play
lr_br=0.1, # -- Some Hyperparameters
lr_avg=0.005,
mini_batch_size_br=128,
mini_batch_size_avg=128,
),
eval_methods={
"br": 2000, # Evaluate Best Response every 2000 iterations
},
)
ctrl.run()
For deployment on AWS, whether single-core, many-core distributed, or on a cluster, please first follow the tutorial in the corresponding section of PokerRL's README.
We recommend forking this repository so you can write your own scripts but still have remote access through git.
In your run-script set either the DISTRIBUTED or the CLUSTER option of the TrainingProfile to True
(see e.g. NFSP/example_distributed.py).
Moreover, you should specify the number of LearnerActor and evaluator workers (if applicable) you want to deploy.
Note that hyperparmeters ending with "_per_la" (e.g. the batch size) are effectively multiplied by the number of
workers.
When running in DISTRIBUTED mode (i.e. one machine, many cores), simply ssh onto your AWS instance, get your code
onto it (e.g. through git cloning your forked repo) and start your run-script.
To fire up a cluster, define a .yaml cluster configuration that properly sets up your workers. Each of them
should have a copy of your forked repo as well as all dependencies on it.
Use ray up ... in an ssh session to the head of the cluster to start the job - more detailed instructions about
the underlying framework we use for distributed computing can be found at ray.
If you use this repository in your research, you can cite it by citing PokerRL as follows:
@misc{steinberger2019pokerrl,
author = {Eric Steinberger},
title = {PokerRL},
year = {2019},
publisher = {GitHub},
journal = {GitHub repository},
howpublished = {\url{https://github.com/TinkeringCode/PokerRL}},
}
- Eric Steinberger
This project is licensed under the MIT License - see the LICENSE file for details.
[1] Heinrich, Johannes, and David Silver. "Deep reinforcement learning from self-play in imperfect-information games." arXiv preprint arXiv:1603.01121 (2016).