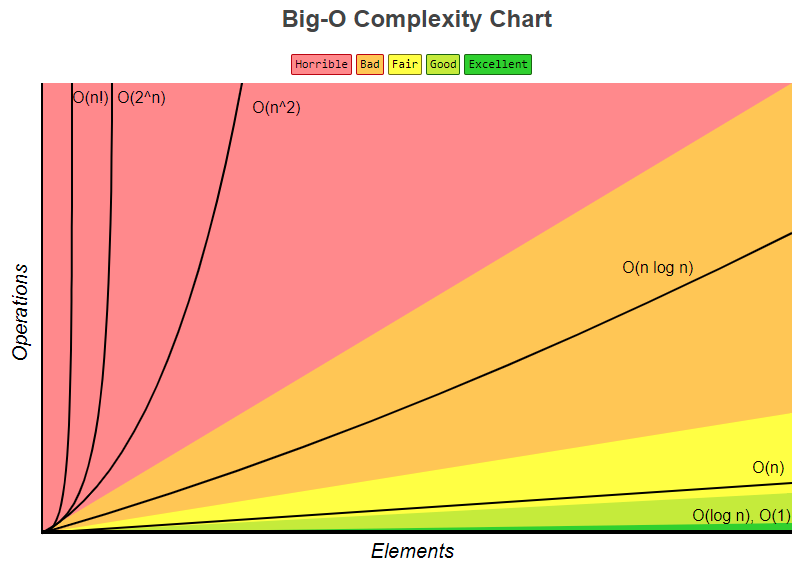
In a nutshell, Big-O is a rating for the complexity of the algorithm based on the cost or processing time.
Big-O notations are mathematical notations that can be used to describe the complexity of the algorithm.
There is no growth in the number of operations as it does not depend on the volume of input data (n).
The growth in the number of operations is less than the growth in the number of items.
The growth in the number of operations is directly proportional to the growth in the number of items.
It is the result of operations (log n) performed n times.
Occurs when data items are processed in pairs, often with repetitions within each other.
As n increases, the analyzed factor (time or space) increases exponentially.
The number of executed instructions grows very quickly for a small amount of data.
| Big-O | Alternative |
|---|---|
| O(1) | O(yeah) |
| O(log n) | O(nice) |
| O(n) | O(ok) |
| O(n log n) | O(uch) |
| O(n^2) | O(my) |
| O(2^n) | O(no) |
| O(n!) | O(mg!) |