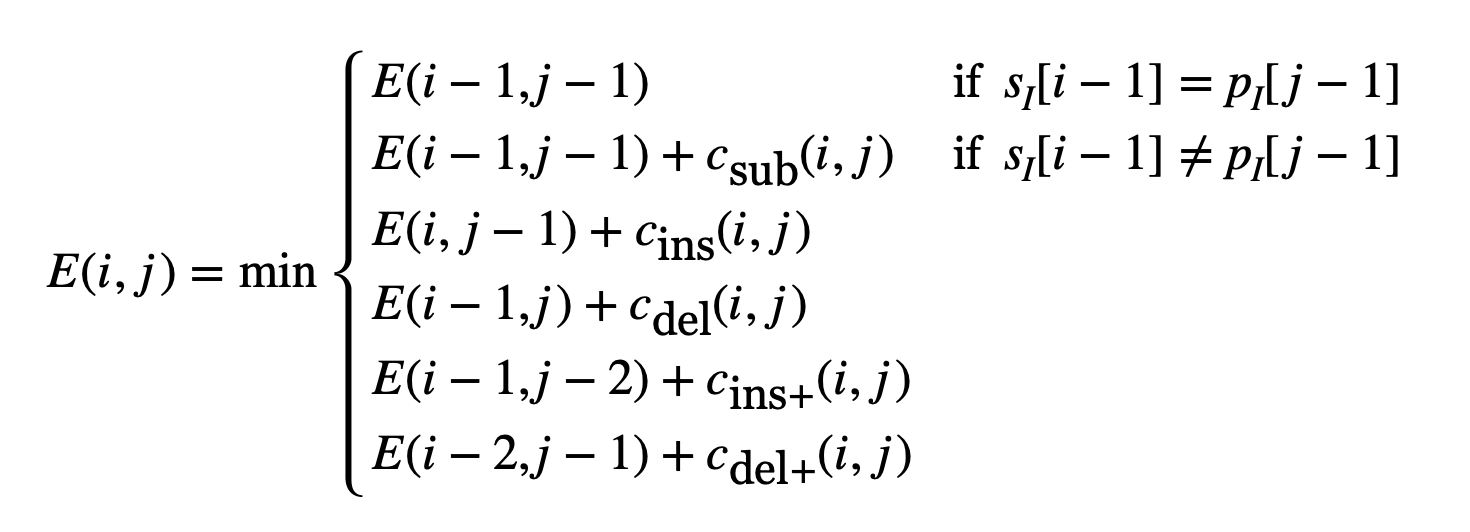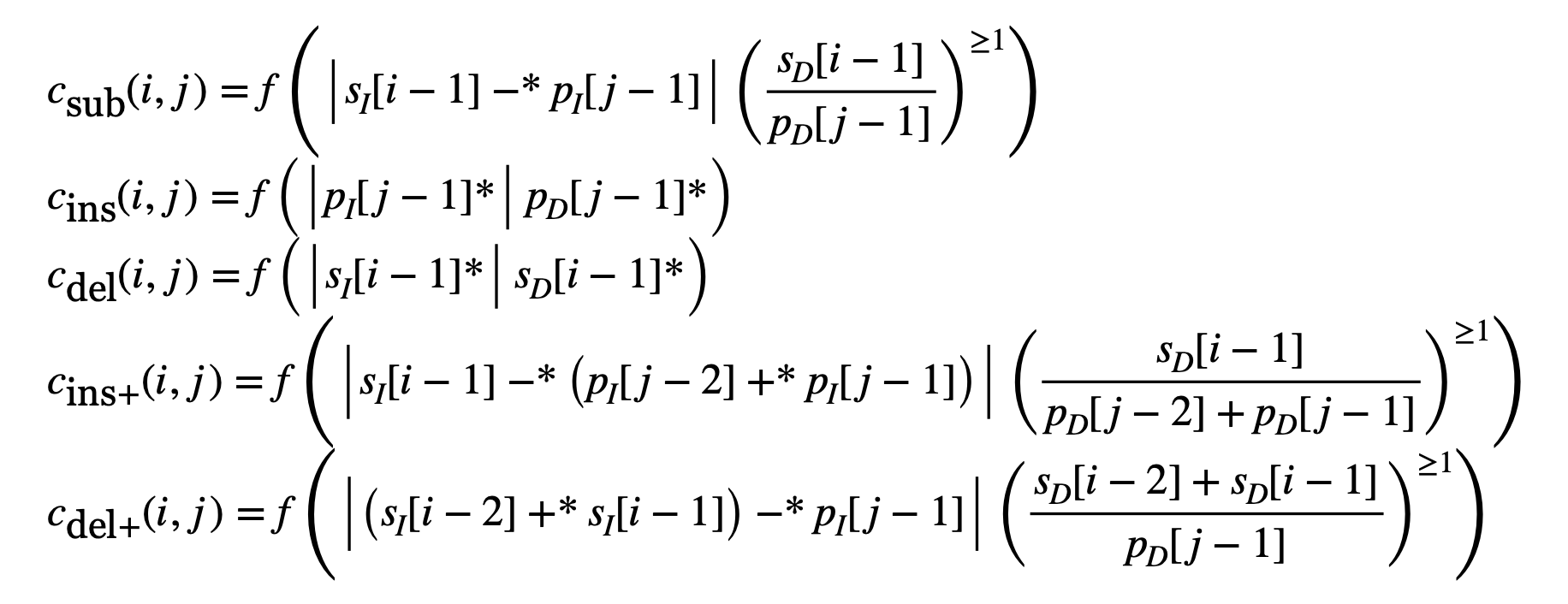FugueStat

Perform visual music-based fugal analysis using subjects, countersubjects, and their transformations.

FugueStat

Setup

Requires: python-3.10+

Create virtual environment:

pip install virtualenv
virtualenv -p python3 venv3
source venv3/bin/activate

Install supplementary libraries:

pip install -r requirements.txt

Libraries: pyyaml, numpy, pytest

Usage

python3 main.py <file_name>.<file_extension> \
  [--reversal] [--inversion] [--reversal-inversion] \
  [--augmentation] [--diminution] [--all] \
  [--debug] [--logfile=log.txt] [--help]

--reversal or --rev should be set for reversed subject to be matched.
--inversion or --inv should be set for inverted subject to be matched.
--reversal-inversion or --rev-inv should be set for reversed-inverted subject to be matched.
--augmentation or --aug should be set for augmented subject to be matched.
--diminution or --dim should be set for diminished subject to be matched.
--all should be set for detection of all currently supported transformations.
--debug should be set for debug logging to be transmitted to --logfile.
--logfile should be set to the location of the log file to write to.
--help displays the same such descriptions.

Resulting file is found at <file_name>_annotated.<file_extension>.

Prerequisites (temporary)

Music file should only contain 1 single fugue $^1$
No voice discontinuities should occur where a stream of notes is intuitively continuous within a single voice $^2$
Fugue should begin with a single solo voice stating the subject
A time signature is required for all measures

$^1$ This condition can be relaxed in the future by requiring titles of fugal sections to contain certain keywords.

$^2$ Mentioned in TO-DO List, some alleviation will be provided through intelligent voice joining, but try best to avoid this issue.

File import and export

The current supported file reading and writing formats are:

.musicxml

Terminology

Fugue: A contrapuntal composition in which a short melody or phrase (the subject) is introduced by one part and successively taken up by others and developed by interweaving the parts.

Notable examples for solo piano:

Johann Sebastian Bach: Well-Tempered Clavier 1 & 2 (48 fugues total of all key signatures)
Ludwig van Beethoven: Grosse Fuge, Op. 133
Ludwig van Beethoven: Piano Sonata No.28, 29, 31
Dmitri Shostakovich: 24 Preludes and Fugues, Op. 87
Karol Szymanowski: Piano Sonata No.2, 3
Elliott Carter: Piano Sonata
Kaikhosru Shapurji Sorabji: Opus Clavicembalisticum (+ many others)

(I currently work on the most accurate solo piano performance rendition of "Opus Clavicembalisticum" in history.)

Voice: In a contrapuntal composition, a contiguous and related series of notes which forms a single layer. Like a human voice, it is often both independent and dependent on the concurrent progression of other voices. The majority of fugues are written with 3-4 voices, though some by Kaikhosru Sorabji can go up to 8 concurrent voices.

Interval: The semitone distance between any two notes. + for ascending, - for descending.

Subject: A musical theme introduced as a solo voice at the start of a fugue. The subject is the main focus of the fugue and can undergo subtle to dramatic alterations and transformations as the fugue progresses.

Alterations include:

Entire translation up/down in pitch
Decreasing/increasing 1 or more intervals' sizes.
Contiguous partial statement of the subject/countersubject.
Inserting/deleting a small number of notes from fugal elements.

Transformations include:

Reversal: Stating the subject with all the intervals in reverse order.
Inversion: Stating the subject with all the intervals' directions inverted.
Reversal & Inversion: Stating the subject with simultaneous reversal and inversion.
Augmentation: Stating the subject where each note's duration is 2 or more times longer in duration.
Diminution: Stating the subject where each note's duration is 2 or more times shorter in duration.

Countersubject: Material articulated by a second voice which accompanies the second statement of the subject immediately after the first statement completes.

Countersubjects can undergo similar alterations and transformations as the subject.

Problem

In standard music theory, common tasks include performing manual analysis of fugal elements in a piece of music either for academic purposes or to aid in the process of learning to play such pieces of music. Typically, such procedures, done manually, are completely manageable within a reasonable timeframe and have very high accuracy as identification of fugal elements are, more intuitively, a human task. However, personally being a greenfield performer of Kaikhosru Sorabji's solo piano works which often contain fugues ranging from 10 minutes to 2 hours in length along with some of the most complex contrapuntal conceptions in all of history, automated analysis could save a massive amount of time.

Example: Fugue 1's subject from Bach's Well-Tempered Clavier 1

Example: Contrapuntally dense section from Fugue 1 from Bach's Well-Tempered Clavier 1

With increasing complexity, this process becomes much less trivial (yes, that is solo piano):

Example: "XI. Fuga IV [Dux Tertius]" from Sorabji's Opus Clavicembalisticum

Solution

The solution is inspired by the domain of fuzzy string matching. Fuzzy string matching involves determining whether two strings $A$ and $B$ have some degree of close enough similarity to be considered a match. Applications commonly include DNA sequencing and auto-correction. e.g. "heapt" has close resemblance to "heart".

The metric for closeness I employ in my algorithm design is the well-known edit distance, with many alterations to account for the additional requirements that matching music notes imposes.

However, unlike typical applications of edit distance, it is not matched based on the absolute pitch of each note. Because the entire nature of a fugue consists of modulation to other keys and thematic exploration, it is to be expected that entire translations of the initial subject is the norm. Thus, the intervals between the notes encode more information than the notes themselves.

Using the sequence of intervals as the basis for fuzzy matching, it's now possible to account for interval contractions/dilations in subsequent subject statements. One can think also of this as "soft" matching.

Another factor which contributes to the matching process is the durations of the notes themselves. While intervals may contribute to the majority of the accuracy provided by the matching algorithm, only note duration will be able to provide distinction between a subject statement and both a mere stream of supporting notes and transformations such as augmentation and diminution. Thus, intervals and durations must be combined together in an intuitive way which captures the expected matching behaviour.

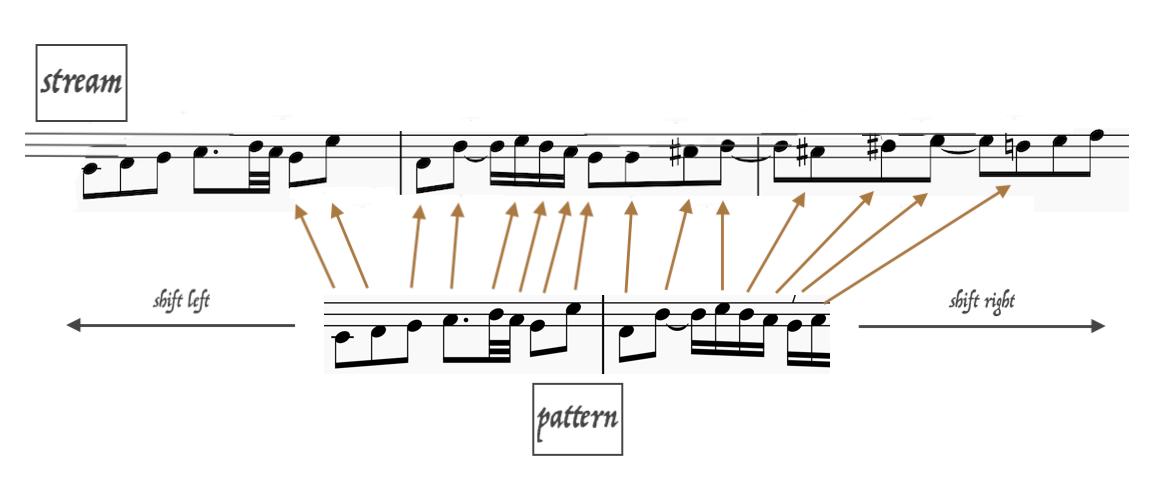
In the code and here, we will refer to a voice as a note sequence or stream. The subject is synonymously called the pattern. The stream is almost always longer than the pattern, and like its name suggests, the stream continuously provides a window (i.e. a buffer) for the pattern to iteratively match over the entire piece of music. Again, recall that the intervals and durations are used, not the absolute pitches. Let's refer to the length of the sequence of intervals for the stream and pattern to, respectively, be $S$ and $P$. Note, it should be apparent that, in code, voices are treated as separate entities as note sequences and are processed independently, even though notes do coincide between voices.

There are two clear issues with what is shown above. Because note insertion/deletion is possible for the stream, a window size fixed to the length of the pattern is insufficient to capture all likely alterations. Thus, a reasonable assumption to make is that the number of matched notes in the stream is at most some factor $n$ times the size of the pattern sequence intervals $P$. A typical factor is $2$, but circumstances may require such factor to be slightly less than $2$. Another issue is that sequential step-by-step iteration of the pattern over the stream is far too inefficient and uses too many unnecessary comparisons when, visually, one can tell that various parts of the pattern are distinct.

There are three levels to the entire algorithm. The lower-level algorithm does something analogous to fuzzy substring matching, the higher-level algorithm controls optimized window propagation, while the final wrapper on the higher-level algorithm uses weighted interval scheduling to select the best transformations to highlight.

Window matching

Let us assume we have a stream window of length $2P$ and pattern length $P$. A typical implementation of edit distance between the stream and pattern calculates the distance between both entire sequences. The issue with this approach is that intermediate edit distance values calculate distance from the start of the stream, which would include costs that are irrelevant.

Assuming the memoization matrix is of dimension $(S + 1) \times (P + 1)$, a known solution is to begin the algorithm by filling the first column with $0$ (to indicate $0$ cost of shifts) and the typical cumulative sum of costs of each interval and duration value in the pattern sequence for the first row. The matrix is then filled bottom-up based on the diagram below and associated recurrence relation where the stream and pattern are denoted s and p respectively. Edit distance function is denoted by $E$. Furthermore, $s_I$ and $s_D$ denote stream intervals and stream durations, and $p_I$ and $p_D$ denote pattern intervals and pattern durations.

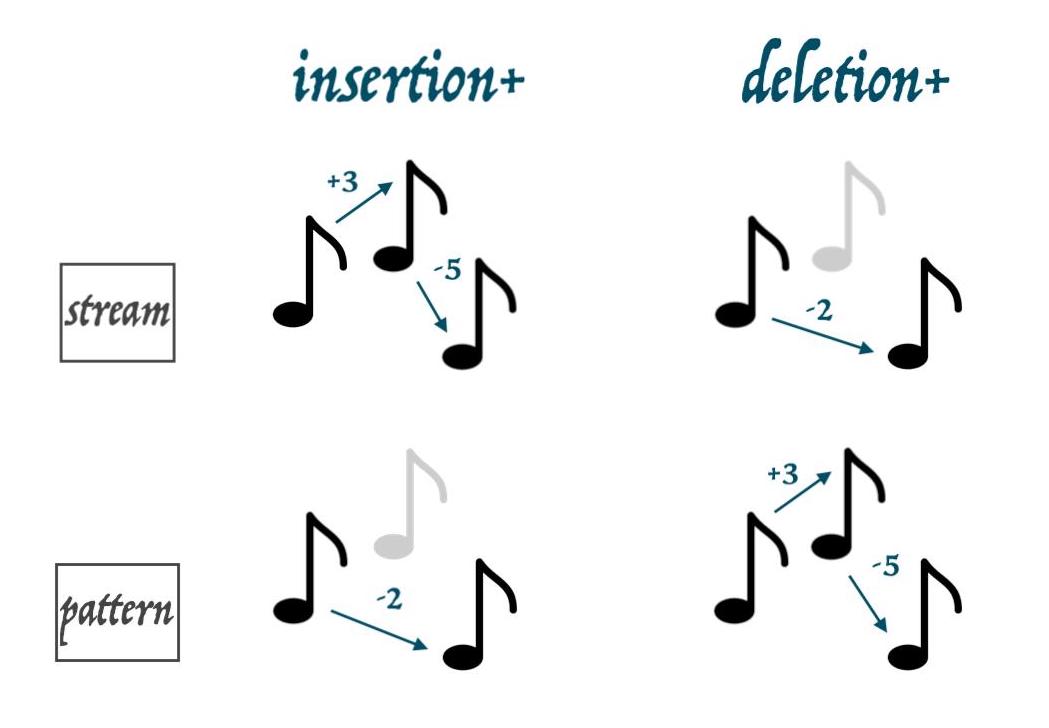
Observe that, unlike typical edit distance, there are two additional cases at the bottom which are unique to this context. $c_\text{sub}$ refers to the substition of an interval, i.e. contraction/dilation. $c_\text{ins}$ and $c_\text{del}$ are typical necessary edit distance computation features. $c_\text{ins+}$ accounts for the case of note insertion and $c_\text{del+}$ accounts for the case of note deletion. The formal definition of the various costs:

Operators and values marked with an asterisk denote edge case handling for rests in the music where intervals are not applicable (i.e. interval between note and rest does not exist). These edge cases are important and do actually affect the outcome of the matching results.

Absolute differences between the intervals are used to model interval similarity. Expressions marked with $\ge 1$ are something I call absolute divisors. They are the multiplicative analog of the idea of absolute difference. The numerator and denominator are chosen from the arguments such that the expression evaluates to a number $\ge 1$. This helps scale the costs in proportion to the durations of the notes being compared.

Finally, a scaling function $f$ is applied to the absolute difference to level off cost as the difference grows. The function is typically $f(x)=\sqrt{cx}$ for some $c\in\mathbb{N^+}$ to avoid one single large interval deviation from preventing the pattern from matching.

The visual motivation for the definitions of $c_\text{ins+}$ and $c_\text{del+}$ are shown below. "Insertion" and "deletion" are just arbitrary semantics in this case, but the idea for the costs are based off of the observation that the compression of the intervals as a result of the added note should sum up to remain constant as before.

Finally, the last step in this lower-level part of the algorithm is to retrieve the entry in the matrix with the lowest edit distance while maximizing match length. This is done slightly differently than normal, and is instead done by first computing the highest index entry of the lowest edit distance value of the last column of the matrix. The last column represents the substring edit distance between each of stream[:1], stream[:2], ..., stream[:S] and pattern. In more concise terms, the starting match index is:

(i, j) := (S - np.argmin(np.flip(memo[:, -1])), P)

However, notice that this initial pair of indices forces the entire pattern to be matched, which isn't always the case since a partial subject match is also possible. Thus, if the adjacent indices listed below (top and left) contain a strictly smaller $E$ value, then move (i, j) to that new position. Rince and repeat until the position is stable. It must be strictly smaller as an equal value doesn't optimize to a maximum number of stream and pattern values. The final value of (i, j) is used as s[:i] and p[:j] and is the right-truncated substring match of pattern for stream. This is not the optimal answer, but the next section will cover how to get it.

Window propagation

As concluded at the end of the previous section, the modified edit distance algorithm computes the right-truncated substring match of pattern for stream. Let us denote this by $M(s,p)$.

This next step kills two birds with one stone. With the initial inspiration being the Knuth-Morris-Pratt (KMP) algorithm, which is one of the most widely implemented practical hard (vs. soft) string matching algorithms, this step can effectively replace a usage of KMP for efficient window propagation.

As a side note, a sliding window is preferred over using the KMP algorithm since the former method offers, in essence, a large lookahead distance while the latter does not. Because partial matches, as a result of sequentially incrementing the matching process, may have so-called "local minimums" in the total match cost, a sliding window approach offers "momentum" to the matching process, thus maximizing the match length; a design choice inspired by momentum-based gradient descent in machine learning.

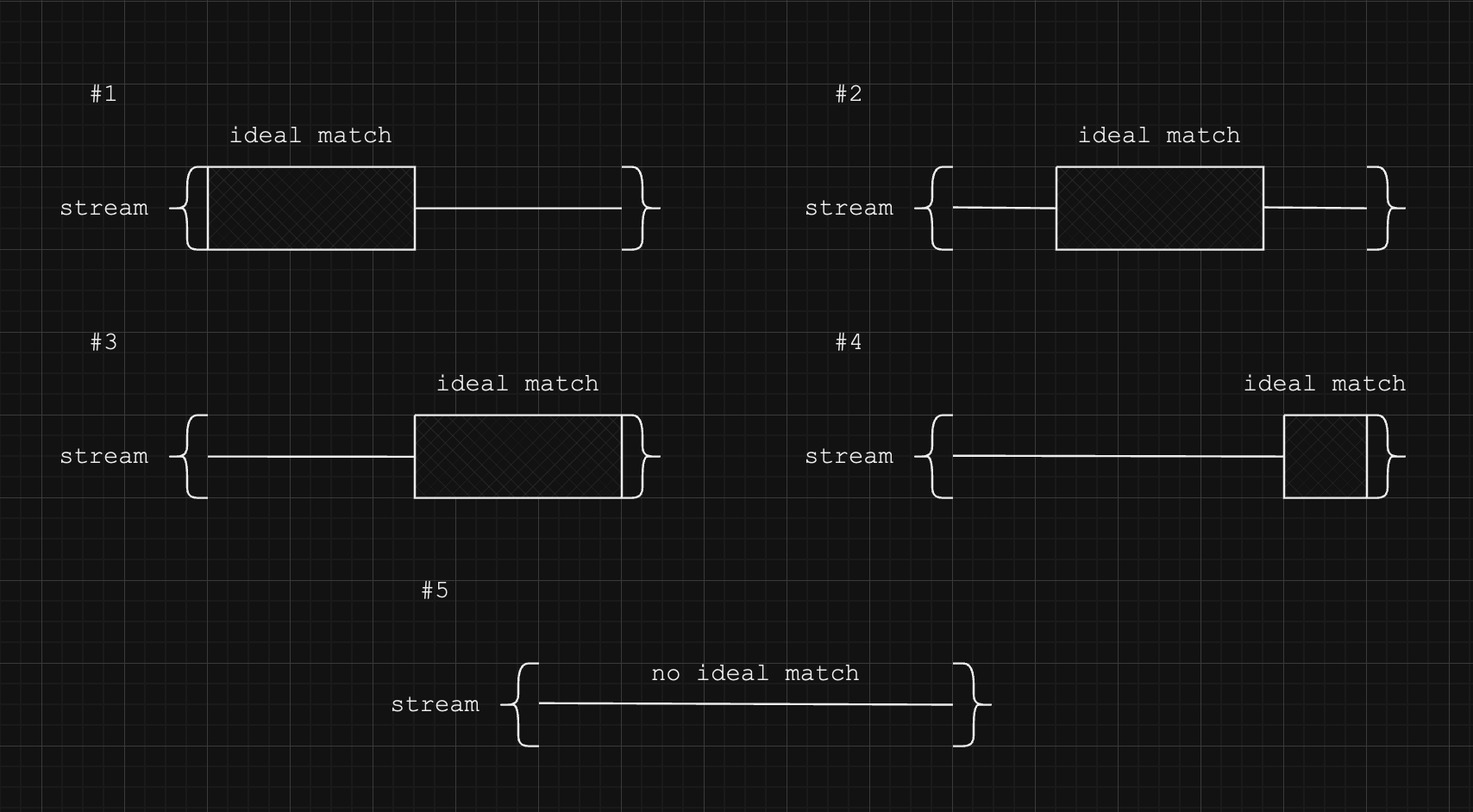
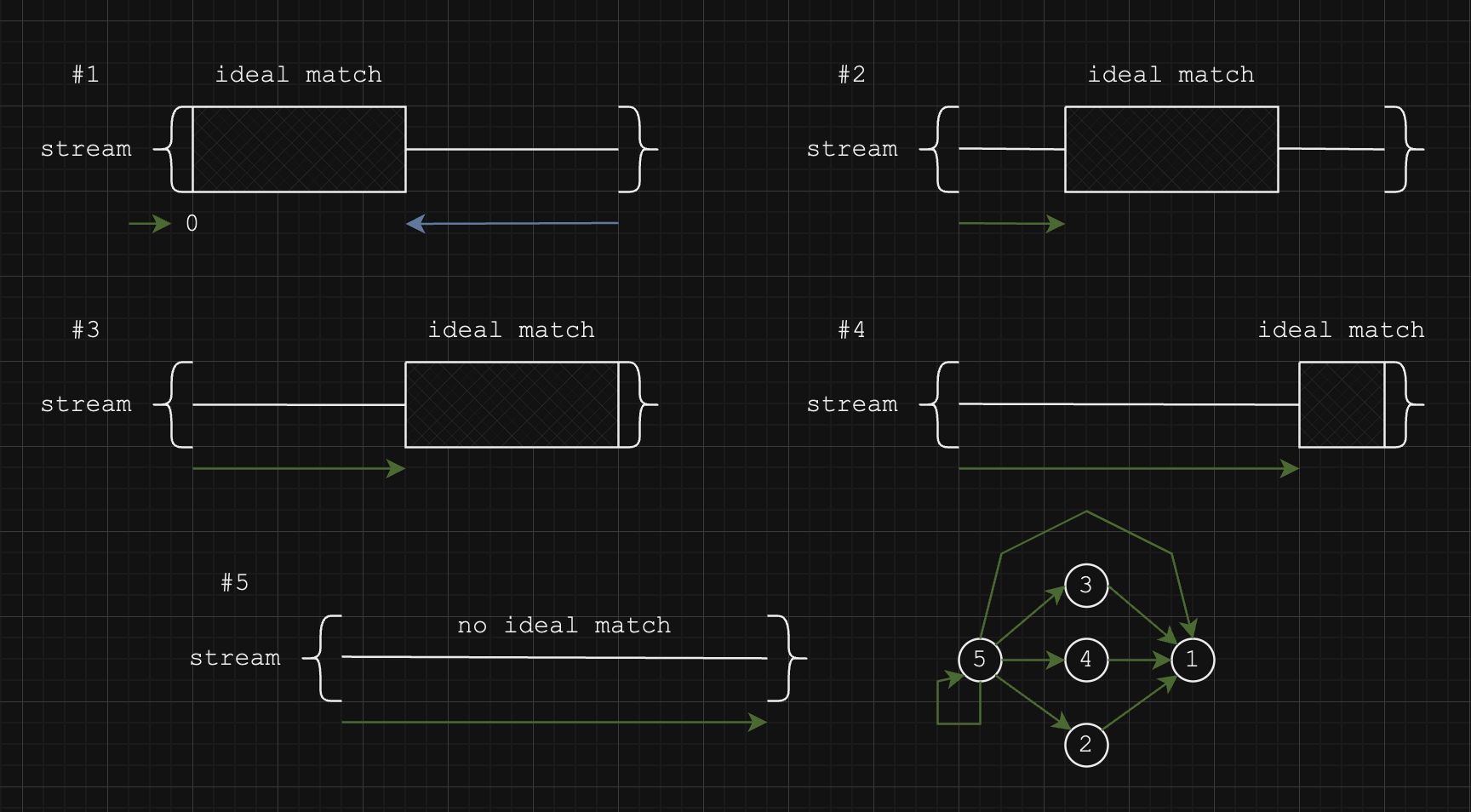
There are 5 orientations for how an ideal pattern match can manifest in a stream. A 6th orientation where the ideal match is cut off on the left side is not applicable, but it'll be clearer why that is the case later.

Because the $M(s,p)$ substring match of stream and pattern is right-truncated, it does not offer the ideal match for case $2, 3, \text{and } 4$. The solution is then to perform a left-truncated substring match of stream and pattern first and then proceed it by a right-truncated version. The left-truncated version is achieved simply by reversing the stream and pattern. The pseudocode is below:

(r_s, r_p) = (s.reversed(), p.reversed())
(r_i, r_j) = M(r_s, r_p);
(s', p') = (r_s[:r_i].reversed(), r_p[:r_j].reversed())
(i', j') = M(s', p')

And, voilà, s'[:i'] is the optimal substring match for p'[:j']. The irrelevant fluff was first stripped from the left and then the other irrelevant fluff was stripped from the right.

How about window propagation? The key to the solution is the fact that a left-truncated substring match was performed first. This procedure can serve both to left-truncate and to propagate to the right. It also serves to left-align the ideal match so the left side of the match isn't cut off by the progressing stream.

The left-truncation algorithm can be repeatedly applied starting at any state $2, 3, 4, \text{or } 5$ until it reaches state $1$, where the right-truncation algorithm finishes things off. In code, this is simply checked by verifying that the offset produced by the left-truncation to be $0$.

And, thus, all the optimal matches are found. The only caveats to this implementation is that after state $1$ completes, the starting position of the stream window is moved forward the length of the match, and after state $5$ completes, only $P$ steps are taken forward, not $2P$.

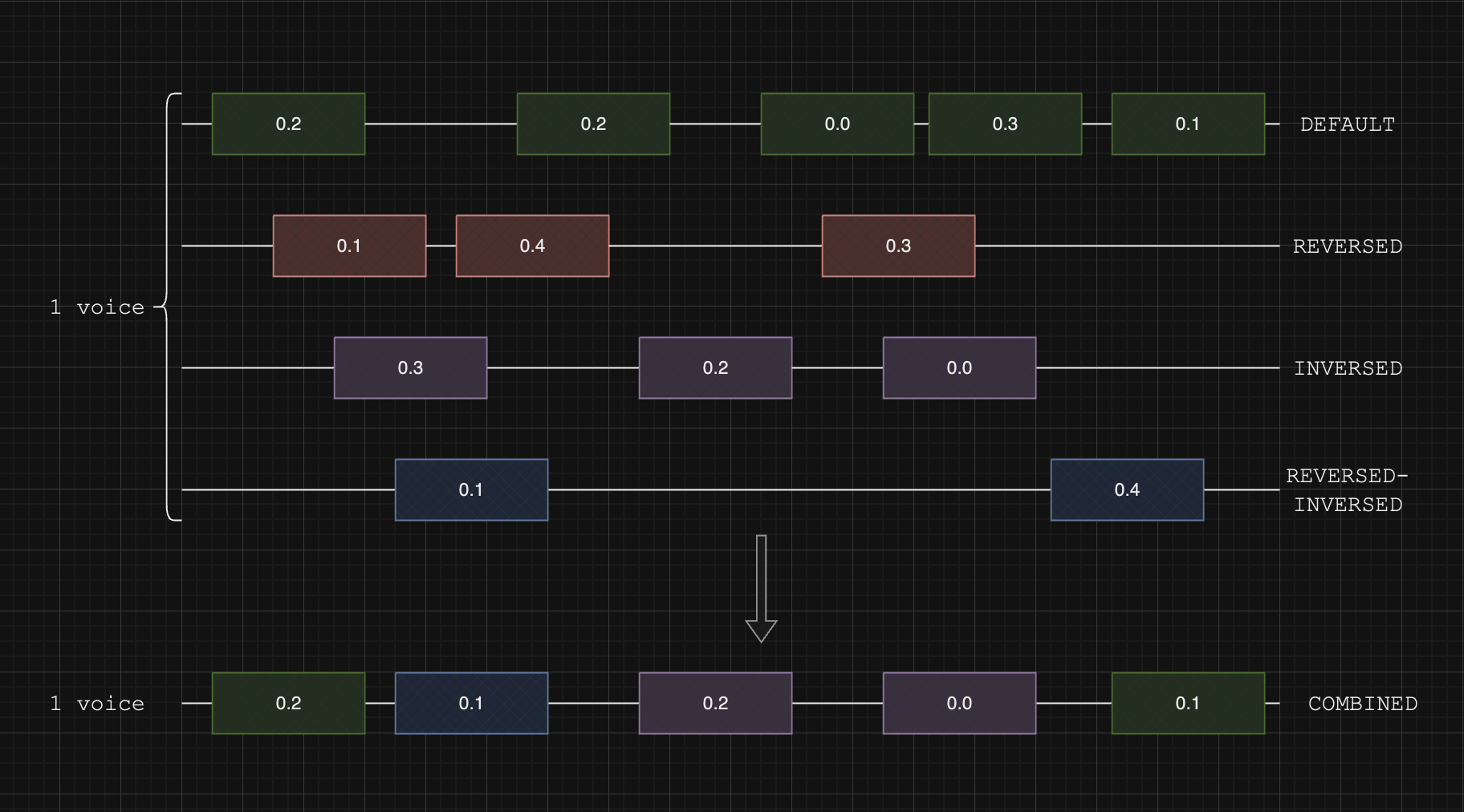
Weighted match scheduling

To accommodate the matching of the various transformations: reversal, inversion, reversal-inversion, augmentation, and diminution, the best non-overlapping matches must be selected.

One of the possible solutions is to compute the modified edit distance for each transformation for each iteration of left-truncation and right-truncation and choose the match with the lowest weight, but this has been found to disrupt the propagation of the stream window in such a way that indeterminate and unintuitive behaviour is the consequence. Therefore, independence between matching for each transformation is sought.

The better and more predictable solution is to fully compute all the matches independently for each transformation and then use a variation of weighted interval scheduling to combine the matches. While a typical implementation of the algorithm would maximize the weight accrued by all the intervals, since the lowest-cost matches are preferred, the cost of each match is instead subtracted from the maximum cost of all matches. This modifies the algorithm to instead minimize the cost while maximizing the number of matches, as shown below:

Such is the result returned for a single voice.

Time complexity

Each window matching iteration is $O(SP) = O(2P * P) = O(P^2)$ due to the computation of edit distance.

Each window matching limit searching procedure is $O(S + P)$.

Each left-truncation operation is proceeded by at most one right-truncation operation. Let $L$ be the voice with the maximum number of notes. Since the shift is proportional to $P$, then the number of window propagation operations is $O\left(\frac{L}{P}\right)$.

Weighted matched scheduling incurs $O\left( \left(\frac{L}{P}\right)^2 \right)$ because at most $\frac{L}{P}$ matches occur per transformation. However, in practise, this contribution is negligible.

So, the total time complexity is $O\left( \frac{L}{P} * S * P + \left(\frac{L}{P}\right)^2 \right) = O\left( \frac{L}{P} * P^2 + \left(\frac{L}{P}\right)^2 \right) = O\left(LP + \left(\frac{L}{P}\right)^2 \right)$. This is an approximate estimate based on empirical evidence.

TO-DO List

$^1$ Mainly because of human score design, at some points, the voice assignment of a relatively continuous stream of notes changes even though it shouldn't. This can cut a subject into pieces across various voices which causes detection to fail. Therefore, at such cut boundaries, try as best as possible to rejoin the pieces.

ExxLiang193/FugueStat