The Kuramoto model (by Yoshiki Kuramoto) describes a large population of coupled limit-cycle oscillators, each with its natural frequency. If the coupling strength exceeds a certain threshold, the system exhibits a phase transition: some of the oscillators spontaneously synchronize, while others remain incoherent. Due to this emergent property, this model and its numerous variations are the main paradigm for synchronization phenomena. The model has been introduced back in 1975 but still today it proves to be an useful and surprising mathematical challenge, that keeps stimulating new advancements in the field.
The goverining system of equations of the model is the following:
A lot of further informations can be found in the report available in the repository.
The main feature of the model is the emergence of synchronization, what is called an emergent property in the field of complex systems. Being also a paradigmatic example of a non-linear dynamical system, the issues related to the stability of the solutions retain a big importance too. It is fundamental also the introduction of stochastic fluctuations in the model, that lead to the Fokker Planck equation in the large population limit. The analysis of the mean field Kuramoto model passes through the identification of a control parameter (the coupling k in this case) and the study of its effect onto an order parameter. The order parameter somehow quantifies the emergent property and it has a central role in the analysis.
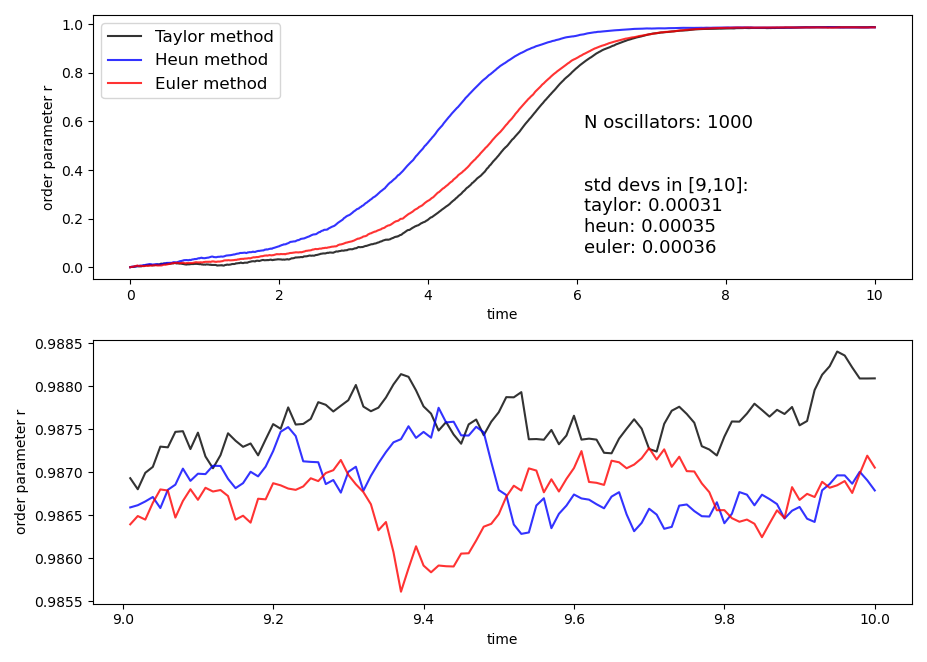
Stochastic dinamical evolution, as integrated by some stochastic numerical schemes:
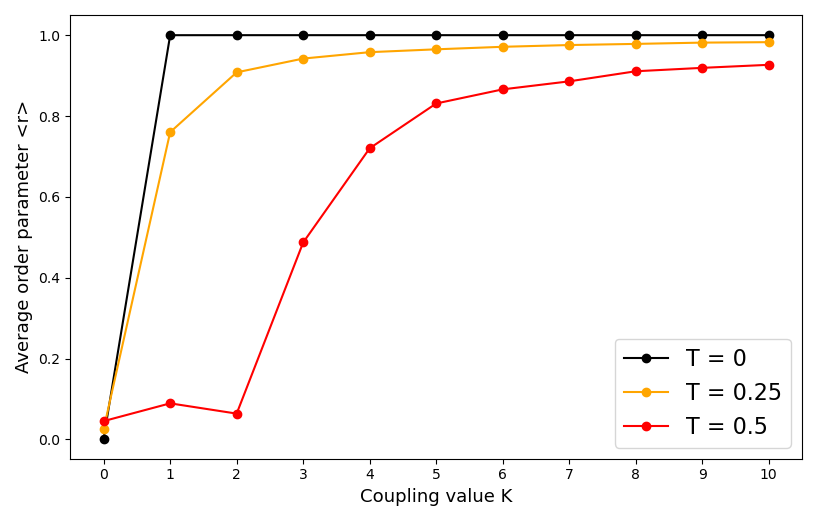
Parameter analysis, in order to spot the rise of synchronization and identify the critical value for the order parameter, all in presence of noise:
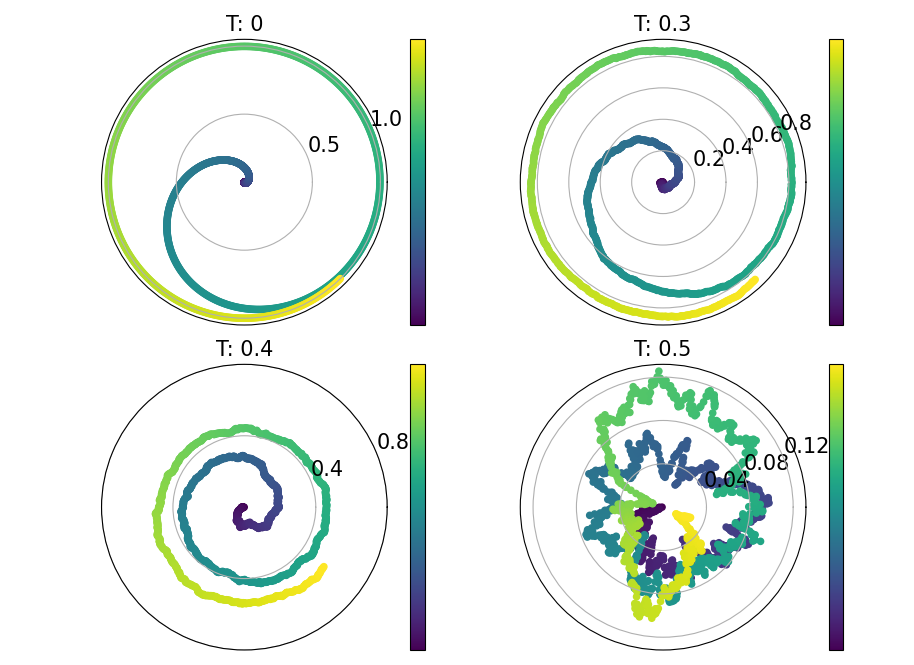
Some polar plots in the complex plane, always cool:
👺 Enjoy! 👹