Haskell library for working with automata, converting DFAs to and simplifying Regular Expressions
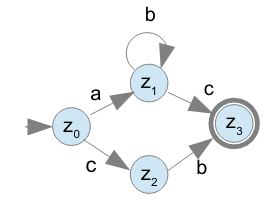
Consider the automaton A = (Q, Σ, δ, q₀, F) where
Q = {0, 1, 2, 3}
Σ = {'a', 'b', 'c'}
δ (0, 1) = 'a'
δ (1, 1) = 'b'
δ (1, 2) = 'c'
δ (0, 2) = 'c'
δ (2, 3) = 'b'
q₀ = 0
F = {3}
With the type DFA being defined as
data DFA = DFA
{ dfaTransitions :: [(State, State, AlphabetElement)]
, dfaFinalStates :: [State]
, dfaState :: State
}
deriving (Show, Eq)automaton A can be represented as
autom :: DFA
autom =
DFA
[ (0, 1, 'a')
, (1, 1, 'b')
, (1, 3, 'c')
, (0, 2, 'c')
, (2, 3, 'b')
]
[3]
0which can then be converted to a regular expression
regexify autom
> RegexOr (RegexConcat (RegexConcat (RegexString "a") (RegexAny (RegexString "b"))) (RegexString "c")) (RegexConcat (RegexString "c") (RegexString "b"))
stringify . regexify $ autom
> "(ab*c|cb)"where the Regex type is defined as
data Regex
= RegexNull
| RegexEmpty
| RegexString String
| RegexAny Regex
| RegexSome Regex
| RegexOptional Regex
| RegexOr Regex Regex
| RegexConcat Regex Regex
deriving (Show, Eq)
Regexify works using the transitive closure method1 to convert DFAs to regular expressions.
To simplify the regular expressions, pattern matching on given rules is used to simplify the expression as far as possible.
This will not always result in the shortest possible expression but it will definitely be an equivalent one.
Currently only DFAs are supported, which also means that δ has to be total, so there cannot be multiple transitions between two states.