Fangtangtang/City-scale-Traffic-Prediction

Multi-stage attention spatial-temporal graph networks for traffic prediction

传统的统计研究方法有：historical average(HA), auto-regressive integrated moving average(ARIMA) and vector auto-regression(VAR)。

前人研究的问题：

1. 对于不同的时间序列来说（如速度、流量），忽略了不同时间序列特征之间的非线性关系。
2. 采用固定的拉普拉斯矩阵来保存位置关系，没有考虑空间关联的动态性。

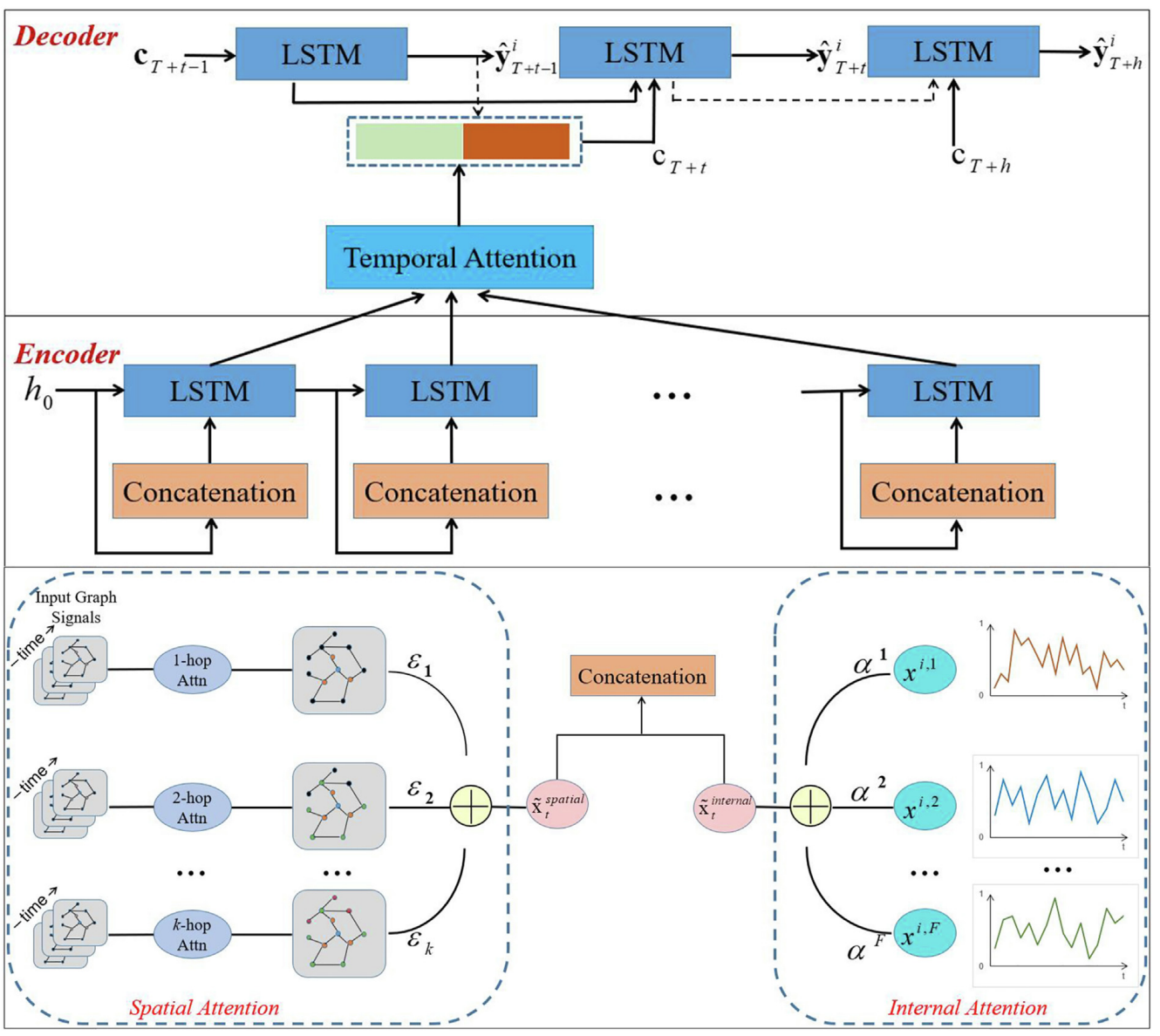
引入三种注意力机制：internal attention，spatial attention and temporal attention。

下面是一些记号：

​ 交通网络**有 $N$ 个传感器节点，每个节点一共记录 $F$ 条时间序列，所以一个传感器的全部数据可以表示为 $\mathbf{X}^i = (\mathbf{x}^{i,1},\mathbf{x}^{i,2}, \dots, \mathbf{x}^{i,F})^{\mathsf{T}}\in \R^{F\times T}$，第 $t$ 时刻的数据为 $\mathbf{x}^i _t = (x^{i, 1}_t, x^{i,2}_t,\dots, x^{i,F}_t)^\mathsf{T}\in \R^F$，对于需要预测的数据表示为 $\mathbf{Y}= (\mathbf{y}^1,\mathbf{y}^2,\dots, \mathbf{y}^N)^\mathsf{T}\in \R^{N\times T}$。

​ 整个交通网络视为一个无向图 $G=(V,E,A)$ ， $A\in \R^{N\times N}$ 表示邻接矩阵。

​ 问题重新表述为提供过去 $T$ 时间的所有节点的数据，预测未来 $h$ 个时刻的数据，$\hat{\mathbf{Y}}=(\hat{\mathbf{y}}^1, \hat{\mathbf{y}}^2,\dots, \hat{\mathbf{y}}^N)^\mathsf{T}\in \R^{N\times h}$，其中 $\hat{\mathbf{y}}^i=(\hat{y}^i_{T+1},\hat{y}^i_{T+2},\dots, \hat{y}^i_{T+h})^\mathsf{T}\in \R^h$。

• Internal attention mechanism:

$$ e_t^p = \mathbf{V}s^\mathsf{T}\cdot \sigma (\mathbf{W}{s1}[\mathbf{h}{t-1};\mathbf{s}{t-1}]+\mathbf{W}_{s2}\mathbf{x}^{i,p}+\mathbf{b}_s)\ \alpha_t^p=\frac{exp(e_t^p)}{\sum exp(e_t^j)} $$

式中 $\mathbf{h}{t-1}\in \R^m$ 和 $\mathbf{s}{t-1}\in \R^m$ 是前一个 Encoder 时间 $t-1$ 的 LSTM 内的状态，$\sigma()$ 表示一类激活函数，$\mathbf{V}s, \mathbf{b}s\in \R^T,\mathbf{W}{s1}\in\R^{T\times 2m},\mathbf{W}{s2}\in\R^{T\times T}$ 都是可学习的参数，最后合并得到 $\tilde{\mathbf{x}}_t^{\text{internal}} = (\alpha_t^1 x_t^{i,1},\alpha_t^2 x_t^{i,2},\dots, \alpha_t^F x_t^{i,F})^\mathsf{T}$

• Spatial attention mechanism:

第一步，所有的节点被分为 $k$ 类，分别是几步能走到目标节点。用 $N_k$ 表示第 $k$ 类节点的数量。

给定目标节点 $i$ ，则节点 $l$ 的注意力结果为 $$ z_t^l = \mathbf{V}{s'}^\mathsf{T}\cdot \sigma(\mathbf{W}{s1'}[\mathbf{h}{t-1};\mathbf{s}{t-1}]+\mathbf{W}{s2'}\mathbf{y}^l + \mathbf{b}{s'})\ \beta_{t,k}^l=\frac{exp(z_{t,k}^l)}{\sum exp(z_{t,k}^j)}\ \beta_{t,k} = (\beta_{t,k}^1,\beta_{t,k}^2,\dots, \beta_{t,k}^{N_k})\in \R^{N_k}\ \varepsilon_{t,k} = w_{t,k}\cdot \beta_{t,k}\ \tilde{\mathbf{x}}_t^{\text{spatial}} = (\varepsilon_t^1 y_t^1,\varepsilon_t^2 y_t^2,\dots, \varepsilon_t^N y_t^N)^\mathsf{T} $$

• Temporal attention mechanism:

$$ r_{t'}^j = \mathbf{V}g^\mathsf{T}\cdot \sigma(\mathbf{W}{g1}[\mathbf{d}{t'-1};\mathbf{s}'{t'-1}]+\mathbf{W}_{g2}\mathbf{h}_j+\mathbf{b}_g) $$

式中 $\mathbf{d}{t'-1}\in \R^n$ 和 $\mathbf{s}'{t'-1}\in \R^n$ 是前一个 Decoder 时间 $t-1$ 的 LSTM 内的状态，$\sigma()$ 表示一类激活函数，$\mathbf{V}g, \mathbf{b}g\in \R^m,\mathbf{W}{g1}\in\R^{m\times 2b},\mathbf{W}{g2}\in\R^{m\times m}$ 都是可学习的参数，经过Softmax得到 $$ \delta_{t'}^j=\frac{exp(r_{t'}^j)}{\sum exp(r_{t'}^l)}\ \mathbf{c}{t'}=\sum \delta {t'}^j\mathbf{h}j $$ Generating the prediciton $$ \text{In encoder:}\ \tilde{\mathbf{x}}t=[\tilde{\mathbf{x}}t^{\text{internal}},\tilde{\mathbf{x}}t^{\text{spatial}}]\in \R^{F+N}\ \mathbf{h}t=f_e(\mathbf{h}{t-1}, \tilde{\mathbf{x}}t), f_e\text{指 LSTM单元}\ \text{In decoder:}\ \mathbf{d}{t'}=f_d(\mathbf{d}{t'-1}, [\hat{y}^i{t'-1}, \mathbf{c}{t'-1}])\ \hat{y}{t'}^i=\mathbf{V}p^\mathsf{T}\cdot(\mathbf{W}{p1}[\mathbf{c}{t'};\mathbf{d}{t'}]+\mathbf{b}_{p2})+b_p $$

Graph Attention Networks

先前的谱方法：

定义度矩阵 $D\in \R^{n\times n}$，邻接矩阵 $A\in\R^{n\times n}$，拉普拉斯矩阵为 $L=D-A$，假设所有的节点信息表示为 $x\in \R^{n}$，$Lx$相当于对所有的节点做了一阶邻居信息的聚合。

对实对称矩阵 $L$做分解 $L= P\Lambda P^\mathsf{T}$， $Lx$ 可以视为以下三个步骤：

1. 傅里叶变换 $P^\mathsf{T}x$
2. 卷积操作 $\Lambda(P^\mathsf{T}x)$
3. 傅里叶逆变换 $P(\Lambda P^\mathsf{T}x)$

在谱域的卷积中，关键的操作是 $\Lambda$，在第一代的谱域图网络 Spectral CNN 中，将特征值处理后的结果 $g(\Lambda)=\left{\begin{matrix}\Theta_1\&\ddots\&&\Theta_n\end{matrix}\right}$视为可学习的卷积。由于没有限定 $g(\Lambda)$ 为多项式，所以需要特征值分解操作，时间复杂度为 $O(n^3)$，而且是全局的，没有利用到数据中经常出现的局部不变性。

通过限定卷积操作为多项式，降低运算量。

$g_\theta(\Lambda) = \theta_0+\theta_1 \Lambda^1+\dots+\theta_k\Lambda^k$，这样 $Pg_\theta(\Lambda)P^\mathsf{T}x=\sum\theta_i L^i x$。好处是参数数量是阶数 $k$ 远小于节点数 $n$，卷积具有局部性，而不是全局性。

可以使用切比雪夫多项式代替原始的多项式，$y=\sigma(\sum \theta_i T_i(\hat{L})x)$，这里为了获得特征值在 $[-1,1]$ 的矩阵，用 $\hat{L}$ 代替 $L$，一种方法为 $\hat{L} = \frac{2}{\lambda_{max}}L-I_N$，另一种方法为 $\hat{L} = L_{normalized}-I_N=D^{-\frac{1}{2}}LD^{\frac{1}{2}}=-D^{-\frac12}AD^{\frac12}$

若取阶数 $k=1$， 则 $$ \sigma(\theta_0+\theta_1(L_{normalized}-I_N)x)=\sigma(\theta_0+\theta_1(-D^{-\frac12}AD^{\frac12})x)\ =\sigma(\theta(D^{-\frac12}\hat{A}D^{\frac12})x) $$ 如果取$\theta_0=-\theta_1, \hat{A}=A+I_N$

Graph attention layer

层的输入为 $\mathbf{h}={\vec{h}_1,\vec{h}_2,\dots,\vec{h}_N}, \vec{h}i\in\R^F$，层的输出为 $\mathbf{h'}={\vec{h'}1,\vec{h'}2,\dots,\vec{h'}N}, \vec{h'}i\in\R^{F'}$，一个共享的权重矩阵作用于每一个节点：$\mathbf{W}\in\R^{F'\times F}$,self-attention:$a:\R^{F'}\times\R^{F'}\to\R,e{i,j}=a(\mathbf{W}\vec{h}i,\mathbf{W}\vec{h}j)$，表示了节点 $j$ 对节点 $i$ 的重要性。只在节点 $i$ 的邻居 $N_i$ 上计算， $$ \alpha{i,j} = \frac{exp(e{i,j})}{\sum{k\in N_i}exp(e{i,k})} $$ 在他们的实现中，$e{i,j} = \text{LeakyReLU}(\vec{a}^\mathsf{T}[\mathbf{W}\vec{h}i;\mathbf{W}\vec{h}j])$ $$ \vec{h}i'=\sigma(\sum{j\in N_i} \alpha{i,j}\mathbf{W}\vec{h}j)\ \vec{h}i=\big{|}{k=1}^K\sigma(\sum{j\in N_i}\alpha{i,j}^k\mathbf{W}^k\vec{h}j)\ \vec{h}i=\sigma(\frac{1}{K}\sum{k=1}^K\sum{j\in N_i}\alpha{i,j}^k\mathbf{W}^k\vec{h}_j) $$

DCRNN:Diffusion Convolutional Recurrent Neural

用带权的邻接矩阵表示图，边权是距离的函数：$\mathcal{G}=(\mathcal{V},\mathcal{E},\mathbf{W})$，用$\mathbf{X}^{(t)}\in\R ^{N\times P}$表示观测的数据。

问题表示为$[\mathbf{X}^{(t-T'+1)},\dots, \mathbf{X}^{(t)};\mathcal{G}]\overset{h(\cdot)}{\to}[\mathbf{X}^{(t+1)},\dots, \mathbf{X}^{(t+T)}]$。

用扩散的过程来表示空间的相关性，用random walk with restart来模拟这一过程。最终的分布为 $$ \mathbf{P}=\sum _{k=0}^\infty \alpha (1-\alpha)^k (\mathbf{D}_O^{-1}\mathbf{W})^k\ $$ 使用扩散的有限$K$步截断，并为每个步骤分配可训练的权重。同时，还应该包括反向扩散过程。文中用$\mathbf{D}$表示无向图的度矩阵，$\mathbf{D}_O$和$\mathbf{D}_I$表示出度、入度矩阵。

这样，扩散卷积为 $$ \mathbf{X}{:,p\star \theta}=\sum{k=0}^{K-1}({\theta}_{k,1}(\mathbf{D}O^{-1}\mathbf{W})^k+\theta{k,2}(\mathbf{D}I^{-1}\mathbf{W}^\mathsf{T})^k)\mathbf{X}{:,p} $$ 其中$\theta\in\R^{K\times 2}$是可学习的参数。

定义卷积层为 $$ \mathbf{H}{:,q}=\mathbf{a}\left(\sum{p=1}^P\mathbf{X}{:,p\star\Theta{q,p,:,:}}\right) $$ 其中$\Theta\in\R ^{Q\times P\times K\times 2}=[\theta]_{q,p}$，$\mathbf{X}\in\R^{N\times P}$是输入，$\mathbf{H}\in \R^{N\times Q}$是输出。

时间依赖性（DCGRU）：

重置门：$\mathbf{r}^{(t)}=\sigma(\Theta_{r\star\mathcal{G}}[\mathbf{X}^{(t)},\mathbf{H}^{(t-1)}]+\mathbf{b}_r)$

更新门：$\mathbf{u}^{(t)}=\sigma(\Theta_{u\star\mathcal{G}}[\mathbf{X}^{(t)},\mathbf{H}^{(t-1)}]+\mathbf{b}_u)$

隐藏状态：$\mathbf{C}^{(t)}=\tanh(\Theta_{C\star\mathcal{G}}[\mathbf{X}^{(t)},(\mathbf{r}^{(t)}\odot\mathbf{H}^{(t-1)})]+\mathbf{b}_C)$

输出：$\mathbf{H}^{(t)}=\mathbf{u}^{(t)}\odot \mathbf{H}^{(t-1)}+(1-\mathbf{u}^{(t)})\odot \mathbf{C}^{(t)}$

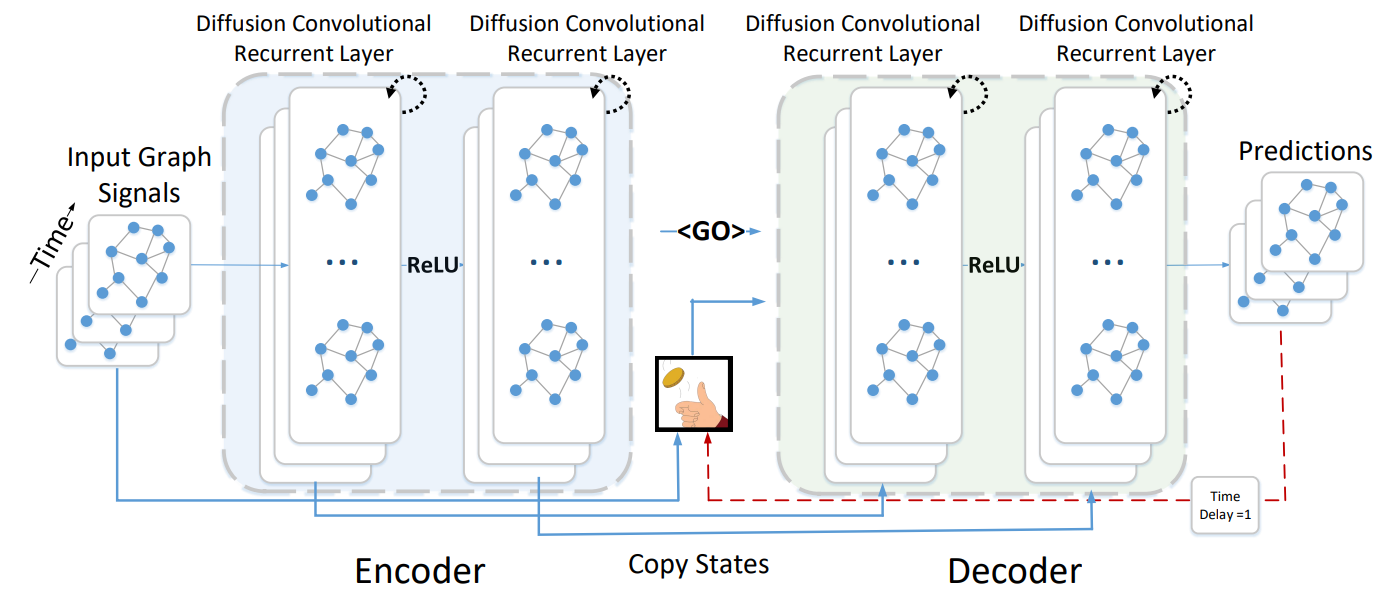
解码器和编码器都是带有DCGRU的循环神经网络。

在训练时：将历史序列输出编码器，并用其最终状态初始化解码器，解码器在给定先前的真实值的情况下生成预测。

在测试时：真实值被模型本身生成的预测所替代。

训练和测试输入分布之间的差异会导致性能下降，缓解这个问题：将抽样集成到模型中，在该模型的第 $i$ 次迭代中，向模型提供概率为 $\varepsilon_i$ 的真实值或爱侣为 $1-\varepsilon_i$ 的模型预测值。在训练的过程中，逐渐减小改概率直到 0 ，让模型学习测试分布。

实验中，邻接矩阵的权值为$W_{i,j}=exp(-\frac{dist(v_i, v_j)^2}{\sigma})\cdot (dist(v_i, v_j)< \kappa)$，$\sigma$ 为所有距离的方差。

Graph Wavenet

Graph Convolution Layer: $$ \mathbf{Z}=\sum _{k=0}^K\mathbf{P}^k\mathbf{X}\mathbf{W}k\ \mathbf{P}=\mathbf{A}/rowsum(\mathbf{A}) $$ Self-adaptive Adjacency Matrix: $$ \tilde{\mathbf{A}}{adp}=SoftMax(ReLU(\mathbf{E}_1\mathbf{E}_2^\mathsf{T}))\ \mathbf{E}1,\mathbf{E}2\in\R^{N\times c}\ \mathbf{Z}=\sum {k=0}^K\mathbf{P}^k\mathbf{X}\mathbf{W}{k1}+\tilde{\mathbf{A}}^k{apt}\mathbf{X}\mathbf{W}{k2} $$ Temporal Convolution Layer:

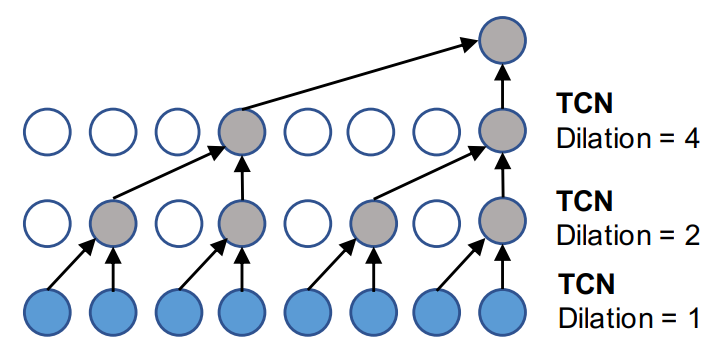
若考虑一维的输入$\mathbf{x}\in\R ^T$和滤波器$\mathbf{f}\in\R^K$ $$ \mathbf{x}\star\mathbf{f}(t)=\sum_{s=0}^{K-1}\mathbf{f}(s)\mathbf{x}(t-d\times s) $$

Gated TCNN: $$ input\ \mathcal{X}\in\R^{N\times D\times S}\ \mathbf{h}=g(\Theta_1\star\mathcal{X}+\mathbf{b})\odot \sigma(\Theta_2\star\mathcal{X}+\mathbf{c}) $$

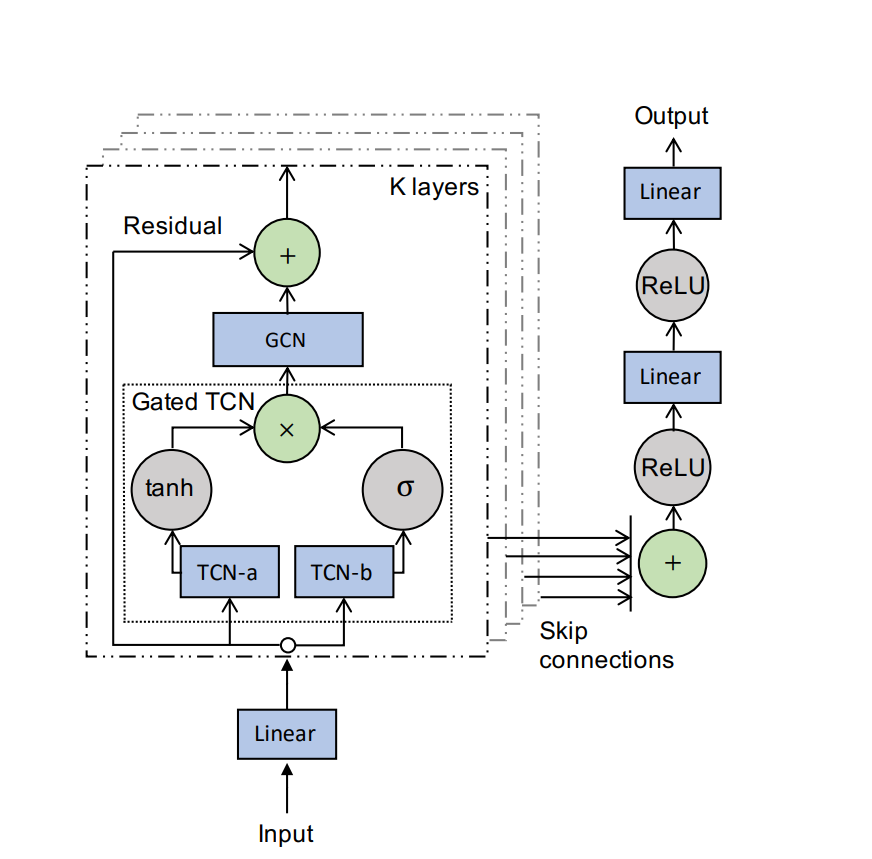
创新点：

1. 提出自学习的邻接矩阵
2. 使用 TCN 替代循环卷积神经网络，通过堆叠 TCN 获取更大的时间感受野

Spatial-Temporal Convolutional Graph Attention Networks(有源码！！)

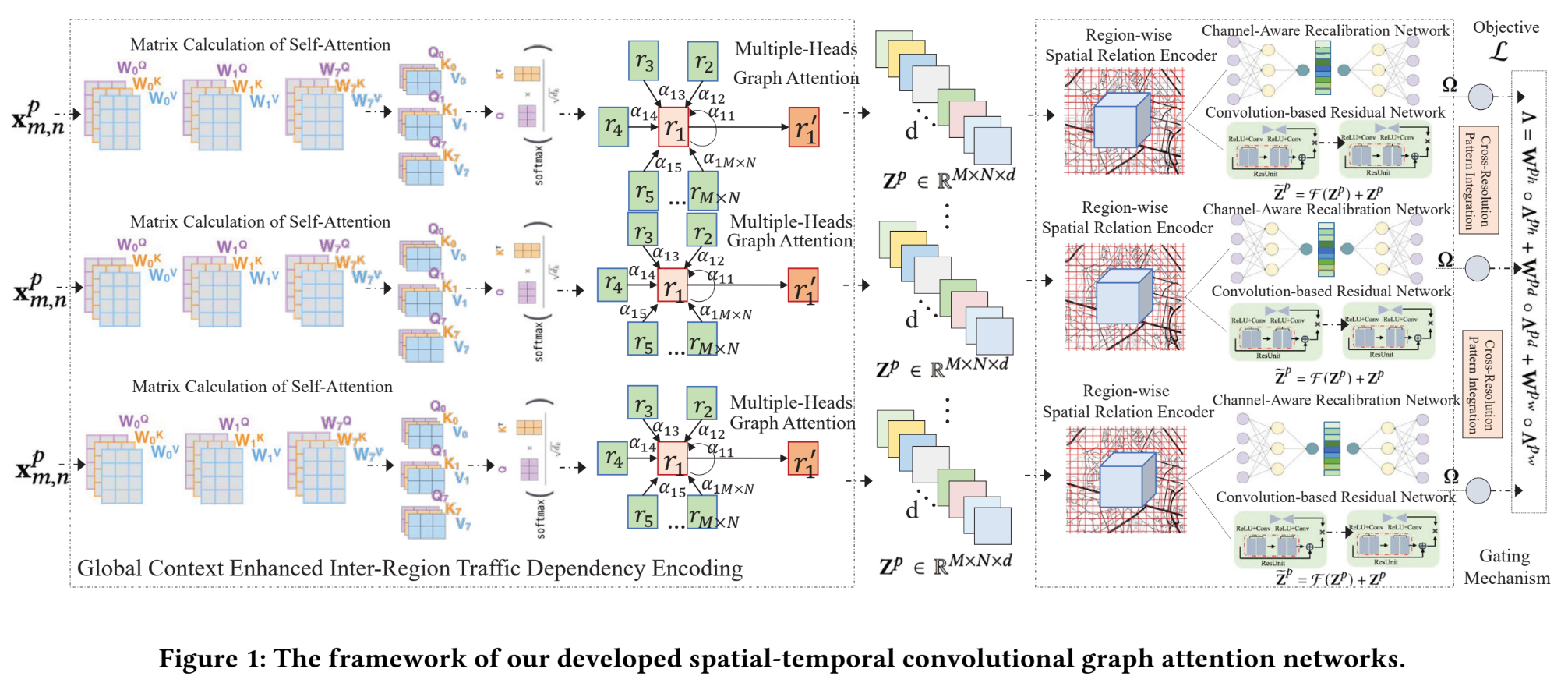
这篇文章用经纬度划分区块为 $M\times N$ 块，用 $X^i \in \R^{M\times N\times T}$ 来表示流入，$X^o \in \R^{M\times N\times T}$表示流出

为了考虑时间颗粒度，用$X^p\in\R^{M\times N\times T_p}$表示按照$p$时间间隔取出来的流，$p$可以取day或者hour等，在这上面做 self-attention layer，$Q\in\R^{|R|\times d}, K\in \R^{|R|\times d},V\in\R^{|R|\times d}$，$Y^p = softmax(\frac{QK^T}{\sqrt{d}})V\in\R^{|R|\times d}$

下面进入空间注意力，输入为$\tilde{Y}^p = Y^p \cdot W_p, W_p\in \R^{d\times d'}$

注意力系数为 $$ \epsilon_{(m,n)(m',n')}=\frac{exp(LeakyReLU(\alpha^T[\tilde{y}^p_{m,n}|\tilde{y}^p_{m',n'}]))}{\sum_{(m',n')\in N(m,n)}exp(LeakyReLU(\alpha^T[\tilde{y}^p_{m,n}|\tilde{y}^p_{m',n'}]))} $$ 将H个多头注意力集中 $$ z^p_{m,n} = |_{h=1}^H LeakyReLU(\sum _{(m',n')\in N(m,n)}\epsilon^h {(m,n)(m',n')}\tilde{y}^p{m,n}) $$ Spatial Relation Modeling between Regions：

1. Convolution-based Residual Unit.

   $\tilde{Z}^p = F(Z^p) +Z^p$，其中F是残差层：

   $Z^{p(l+1)}=ReLU(W^{(l)}\ast Z^{p(l)}+b^{(l)})\in \R^{M\times N \times C}$

2. Channel-Aware Recalibration Network.

   $\Lambda^p=\Omega \circ\tilde{Z}^p=\Omega\circ F(Z^p)+Z^p$

$\Lambda =W^{ph}\circ \Lambda ^{ph}+W^{pd}\circ \Lambda ^{pd}+W^{pw}\circ \Lambda ^{pw}$