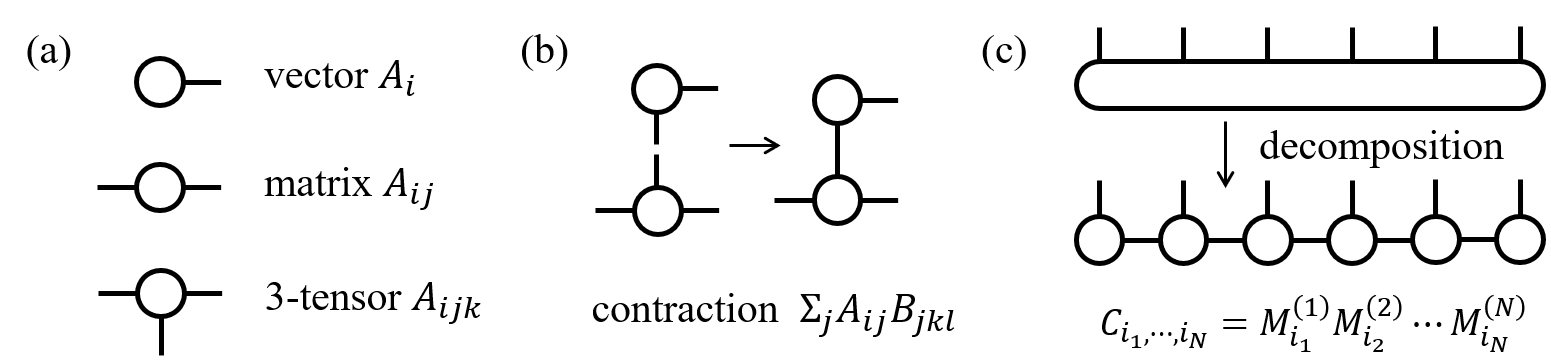
"A pedagogical realization of MPS method."
from AutoMPO.class_fsa import fsa
from AutoMPO.class_named_data import named_data
from AutoMPO.opr_pool import GenSpinOpr
from vMPS.class_mps import mps
if __name__ == "__main__":
# model parameter
N = 5
J = 1.0
g = 0.5
# define operator with a string as name
Sz = named_data('Sz', GenSpinOpr('Sz'))
Sx = named_data('Sx', GenSpinOpr('Sx'))
# construct finite state automata
fsa = fsa(N)
for i in range(0, N):
# add each term in the Hamiltonian
if (i < N - 1):
fsa.Add(J, [Sz, Sz], [i, i + 1])
fsa.Add(g, [Sx], [i])
# use the constructed fsa to generate MPO
list_mpo = fsa.GenMPO()
# visualize MPO represented by operator symbols
fsa.PrintSymbolMPO()
# vMPS/DMRG
D = 4
# construct mps
mps0 = mps(N, D, list_mpo)
# variation
E0, counter = mps0.vMPS(cvg=1e-9, if_print=True, update_sites=2)Matrix product state (MPS) method is a series of powerful algorithms developed to solve a class of Hamiltonians with local interactions, based on the ansatz of “low entanglement”, or “area-law entanglement” precisely. MPS is the 1-dimensional case of tensor network, which plays a central role in modern quantum physics and beyond.
I would like to describe MPS in a nutshell as follows:
- An arbitrary quantum many-body state (1-d, N sites) can be represented as a tensor on a set of certain bases.
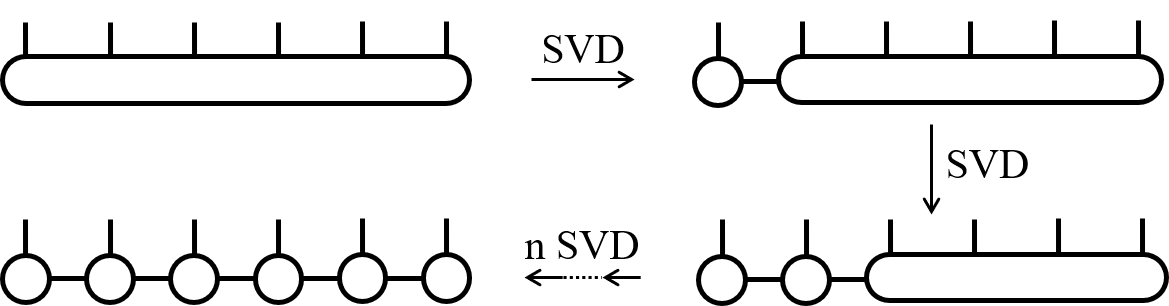
- To solve the difficulty of the exponential growth of Hilbert space dimension with system size, we cut off the state tensor by performing Schmidt decomposition (equivalent to singular value decomposition, SVD) for any partition of the 1-d system and only keeping the data corresponding to the largest D Schmidt weights.
- In this way, we decompose the N-order state tensor as a contraction of N 3-order tensors corresponding to each site approximately, which gives us huge memory savings N×d×D^2 << d^N. Physically, we select a state most like the original one in the “low entanglement” subspace.
- Among a number of algorithms based on MPS, the variational MPS (vMPS) method is the most representative one, which is exactly equivalent with the famed density matrix renormalization group (DMRG) method. The vMPS method can be summarized as: optimizing the energy expectation of MPS by quadratic variation site-by-site (or 2-site) to converge to an approximate ground state. See here for more information.
- Another typical algorithm is the infinite time-evolving block decimation (iTEBD), which evolves an initialized MPS iteratively by an Trotter-decomposed evolution operator.
This repository is dedicated to provide an easy-to-understand implementation of MPS method. A number of ASCII sketches of tensors are presented in the comments to improve readability.
This repository will be updated continually in the near future (07/05/2021).
The author highly acknowledge the guidance from Professor Shuo Yang and her instructive course "Selected Topics in Computational Quantum Physics" in Tsinghua University.