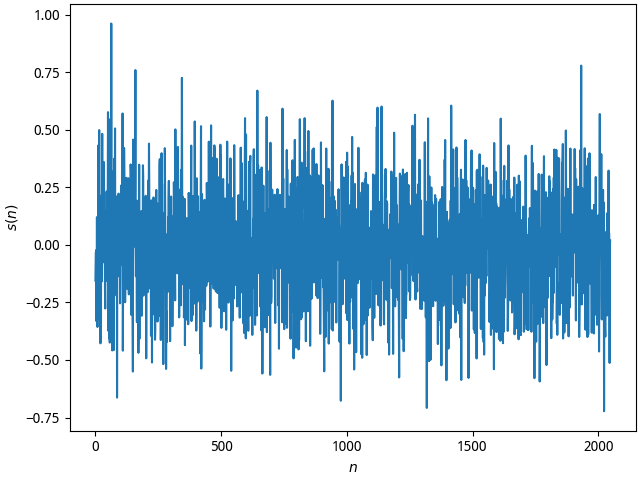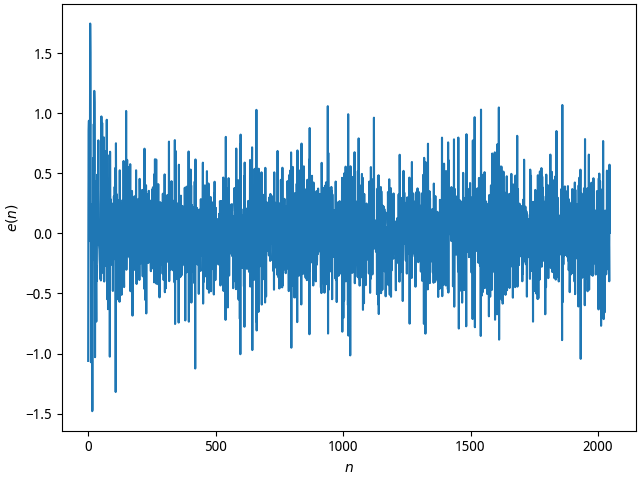CJKmainfont	title	author	institute	documentclass
WenQuanYi Micro Hei	LMS 计算机练习	Wu Zhenyu (SA21006096)	USTC	ctexart

LMS 计算机练习

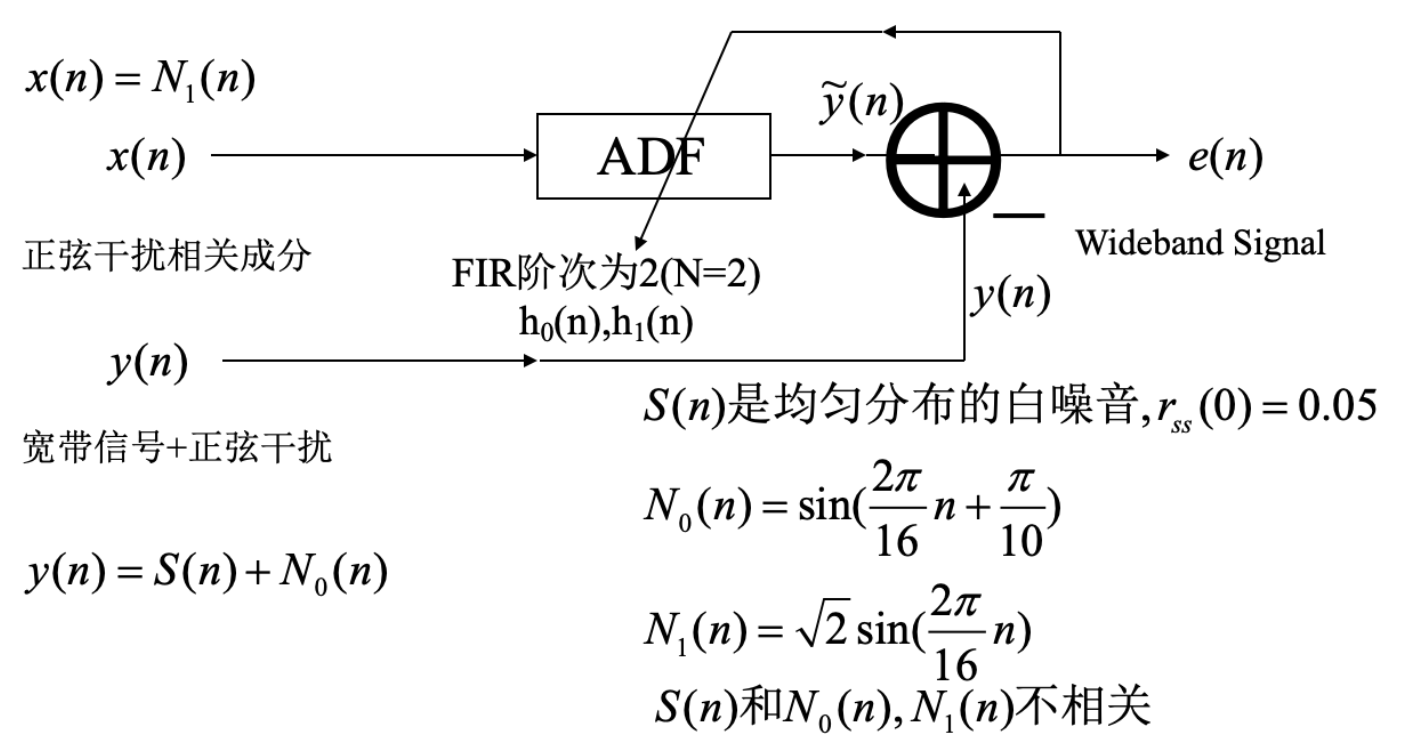
传统的宽带信号中抑制正弦干扰的方法是采用陷波器(notch filter),为此我们需要精确知道干扰正弦的频率.然而当干扰正弦频率是缓慢变化时,且选频率特性要求十分尖锐时,则最好采用自适应噪声抵消的方法.下图是用一个二阶FIR的LMS自适应滤波器消除正弦干扰的一个方案。

1

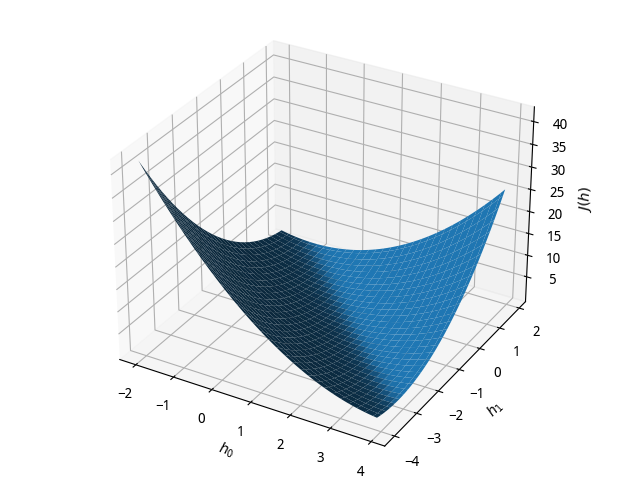
借助MATLAB画出误差性能曲面和误差性能曲面的等值曲线；

等值曲线见题4

2

写出最陡下降法， LMS算法的计算公式($\delta = 0.4$)；

$$\begin{aligned} y & = \mathbf{h}^\mathsf{T}\mathbf{x} + e\ J(\mathbf{h}) & = \mathrm{E}e^2\ & = \mathrm{E}y^2 - 2\mathbf{r}{y\mathbf{x}}^\mathsf{T}\mathbf{h} + \mathbf{h}^\mathsf{T}\mathbf{R}\mathbf{xx}\mathbf{h}\ \frac{\partial{J}}{\partial\mathbf{h}}\Big(\mathbf{h}\Big) & = -2\mathrm{E}e\mathbf{x}\ & = (\mathbf{R}\mathbf{xx} + \mathbf{R}\mathbf{xx}^\mathsf{T})\mathbf{h}

2\mathbf{r}{y\mathbf{x}}\ & = 2\mathbf{R}\mathbf{xx}\mathbf{h}
2\mathbf{r}_{y\mathbf{x}} \end{aligned}$$

Because $\mathbf{R}\mathbf{xx}$ is a Toplitz matrix, We only need to solve $(\mathbf{R}\mathbf{xx})_{k0}$.

where,

$$\begin{aligned} (\mathbf{R}\mathbf{xx}){k0} & = \mathrm{E}i\sqrt2\Big(\sin2\pi\frac{i + k}{16}\Big) \sqrt2\sin2\pi\frac{i}{16}\ & = \cos2\pi\frac{k}{16}\ \mathbf{R}\mathbf{xx} & = \begin{bmatrix} 1 & 0.9239\ 0.9239 & 1 \end{bmatrix}\ (\mathbf{r}_{y\mathbf{x}})_k & = \mathrm{E}i\sqrt2\Big(\sin2\pi\frac{i + k}{16}\Big) \sin(2\pi\frac{i}{16} + \frac{\pi}{10})\ & = \frac1{\sqrt2}\cos(\frac{2\pi k}{16} + \frac{\pi}{10})\ \mathbf{r}{y\mathbf{x}} & = \begin{bmatrix} 0.6725\ 0.5377 \end{bmatrix}\ \mathrm{E}y^2 & = 0.5 + 0.05\ & = 0.55 \end{aligned}$$

So, 最陡下降法：

$$\begin{aligned} \mathbf{h}(n + 1) & = \mathbf{h}(n) - \frac\delta2 \frac{\partial{J}}{\partial\mathbf{h}}\Big(\mathbf{h}(n)\Big)\ & = \mathbf{h}(n) + \delta\mathrm{E}e(n)\mathbf{x}(n)\ & = \mathbf{h}(n) + \delta(\mathbf{r}{y\mathbf{x}} - \mathbf{R}\mathbf{xx}\mathbf{h}(n)) \end{aligned}$$

LMS：

$$\begin{aligned} \mathbf{h}(n + 1) & = \mathbf{h}(n) + \delta e(n)\mathbf{x}(n)\\ \end{aligned}$$

3

用MATLAB产生方差为0.05,均值为0白噪音$S(n)$，并画出其中一次实现的波形图；

4

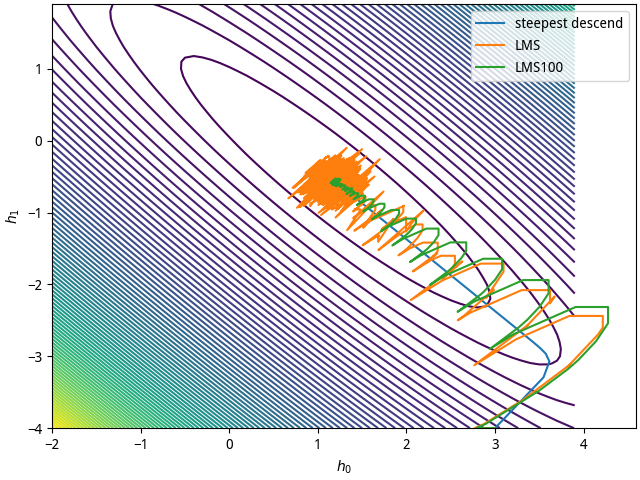
根据2）中的公式，并利用3）中产生的$S(n)$，在1）中的误差性能曲面的等值曲线上叠加画出采用最陡下降法， LMS法时$H(n)$的在叠代过程中的轨迹曲线。

注意，在起点处，LMS先向左移动是正确现象，因为 python 数组从 0 开始，正弦信号在 $n = 0$ 处为 0, 所以第 1 次迭代会有使 1 个方向的下降为 0 。而 matlab 数组从 1 开始，不会有这种现象。

5

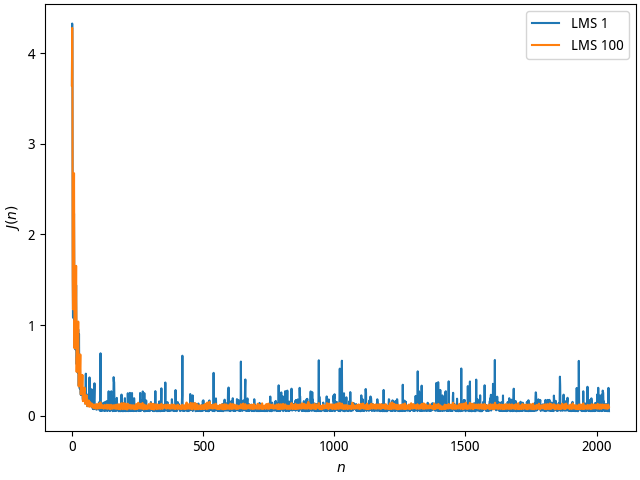
用MATLAB计算并画出LMS法时$J(n) = e^2(n)$随时间$n$的变化曲线（对应$S(n)$的某一次的一次实现）和$e(n)$波形；某一次实现的结果并不能从统计的角度反映实验的结果的正确性，为得到具有统计特性的实验结果，可用足够多次的实验结果的平均值作为实验的结果。用MATLAB计算并画出LMS法时$J(n)$的100次实验结果的平均值随时间$n$的变化曲线。

{#loss}

6

用MATLAB计算并在1）中的误差性能曲面的等值曲线上叠加画出LMS法时100次实验中的$H(n)$的平均值的轨迹曲线；

见题4

7

对以上实验结果给出一些你认为有价值的讨论。

（在实验中$n = 1, \ldots, N$，$N$的取值根据实验情况确定，一般选取足够大以使算法达到基本收敛，本题作业以电子文档PDF格式提供）

LMS 算法收敛速度比最陡下降法慢，在极值点会有严重抖动，可以通过平均缓解抖动。

Freed-Wu/dsp-homework

LMS 计算机练习

1

2

3

4

5

6

7