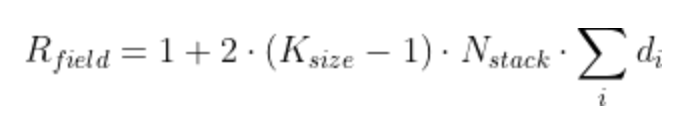Keras TCN

Keras Temporal Convolutional Network. [paper]

Tested with Tensorflow 2.3, 2.4, 2.5 and 2.6.

pip install keras-tcn
pip install keras-tcn --no-dependencies  # without the dependencies if you already have TF/Numpy.

Why Temporal Convolutional Network instead of LSTM/GRU?

TCNs exhibit longer memory than recurrent architectures with the same capacity.
Performs better than LSTM/GRU on a vast range of tasks (Seq. MNIST, Adding Problem, Copy Memory, Word-level PTB...).
Parallelism (convolutional layers), flexible receptive field size (possible to specify how far the model can see), stable gradients (backpropagation through time, vanishing gradients)...

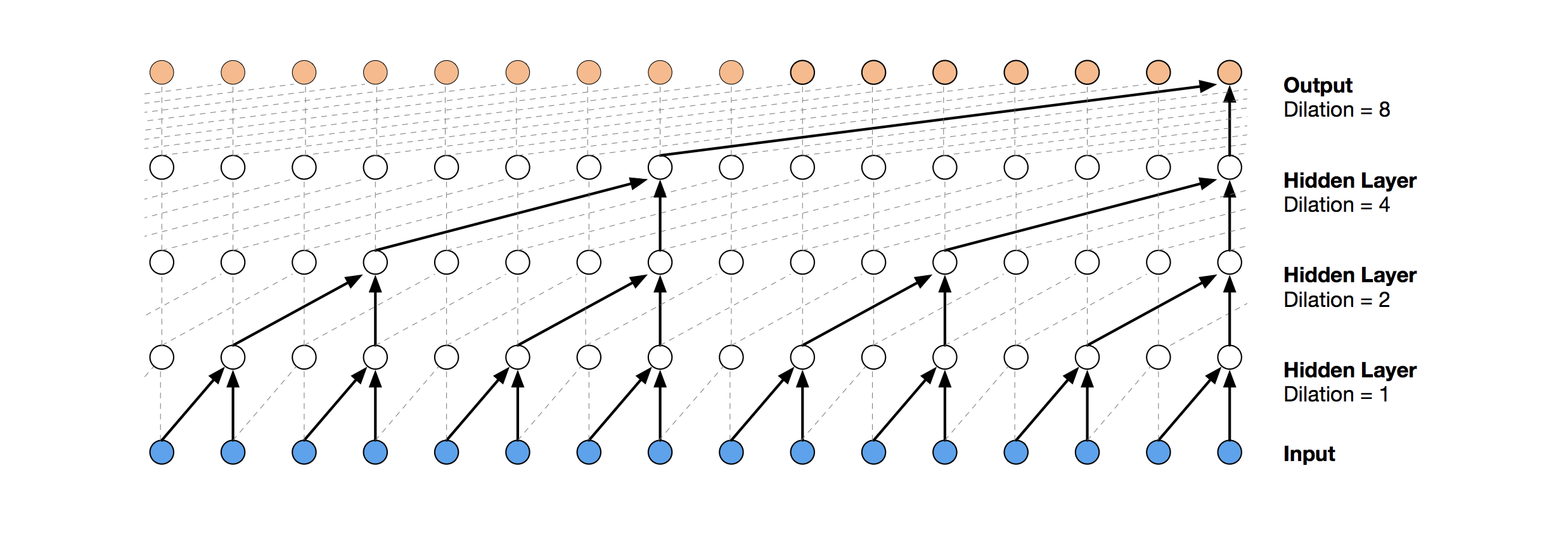Visualization of a stack of dilated causal convolutional layers (Wavenet, 2016)

Index

Keras TCN

API

The usual way is to import the TCN layer and use it inside a Keras model. An example is provided below for a regression task (cf. tasks for other examples):

from tcn import TCN, tcn_full_summary
from tensorflow.keras.layers import Dense
from tensorflow.keras.models import Sequential

# if time_steps > tcn_layer.receptive_field, then we should not
# be able to solve this task.
batch_size, time_steps, input_dim = None, 20, 1


def get_x_y(size=1000):
    import numpy as np
    pos_indices = np.random.choice(size, size=int(size // 2), replace=False)
    x_train = np.zeros(shape=(size, time_steps, 1))
    y_train = np.zeros(shape=(size, 1))
    x_train[pos_indices, 0] = 1.0  # we introduce the target in the first timestep of the sequence.
    y_train[pos_indices, 0] = 1.0  # the task is to see if the TCN can go back in time to find it.
    return x_train, y_train


tcn_layer = TCN(input_shape=(time_steps, input_dim))
# The receptive field tells you how far the model can see in terms of timesteps.
print('Receptive field size =', tcn_layer.receptive_field)

m = Sequential([
    tcn_layer,
    Dense(1)
])

m.compile(optimizer='adam', loss='mse')

tcn_full_summary(m, expand_residual_blocks=False)

x, y = get_x_y()
m.fit(x, y, epochs=10, validation_split=0.2)

A ready-to-use TCN model can be used that way (cf. tasks for some examples):

from tcn import compiled_tcn

model = compiled_tcn(...)
model.fit(x, y) # Keras model.

Arguments

TCN(
    nb_filters=64,
    kernel_size=3,
    nb_stacks=1,
    dilations=(1, 2, 4, 8, 16, 32),
    padding='causal',
    use_skip_connections=True,
    dropout_rate=0.0,
    return_sequences=False,
    activation='relu',
    kernel_initializer='he_normal',
    use_batch_norm=False,
    use_layer_norm=False,
    use_weight_norm=False,
    **kwargs
)

nb_filters: Integer. The number of filters to use in the convolutional layers. Would be similar to units for LSTM. Can be a list.
kernel_size: Integer. The size of the kernel to use in each convolutional layer.
dilations: List/Tuple. A dilation list. Example is: [1, 2, 4, 8, 16, 32, 64].
nb_stacks: Integer. The number of stacks of residual blocks to use.
padding: String. The padding to use in the convolutions. 'causal' for a causal network (as in the original implementation) and 'same' for a non-causal network.
use_skip_connections: Boolean. If we want to add skip connections from input to each residual block.
return_sequences: Boolean. Whether to return the last output in the output sequence, or the full sequence.
dropout_rate: Float between 0 and 1. Fraction of the input units to drop.
activation: The activation used in the residual blocks o = activation(x + F(x)).
kernel_initializer: Initializer for the kernel weights matrix (Conv1D).
use_batch_norm: Whether to use batch normalization in the residual layers or not.
use_layer_norm: Whether to use layer normalization in the residual layers or not.
use_weight_norm: Whether to use weight normalization in the residual layers or not.
kwargs: Any other set of arguments for configuring the parent class Layer. For example "name=str", Name of the model. Use unique names when using multiple TCN.

Input shape

3D tensor with shape (batch_size, timesteps, input_dim).

timesteps can be None. This can be useful if each sequence is of a different length: Multiple Length Sequence Example.

Output shape

if return_sequences=True: 3D tensor with shape (batch_size, timesteps, nb_filters).
if return_sequences=False: 2D tensor with shape (batch_size, nb_filters).

How do I choose the correct set of parameters to configure my TCN layer?

Here are some of my notes regarding my experience using TCN:

nb_filters: Present in any ConvNet architecture. It is linked to the predictive power of the model and affects the size of your network. The more, the better unless you start to overfit. It's similar to the number of units in an LSTM/GRU architecture too.
kernel_size: Controls the spatial area/volume considered in the convolutional ops. Good values are usually between 2 and 8. If you think your sequence heavily depends on t-1 and t-2, but less on the rest, then choose a kernel size of 2/3. For NLP tasks, we prefer bigger kernel sizes. A large kernel size will make your network much bigger.
dilations: It controls how deep your TCN layer is. Usually, consider a list with multiple of two. You can guess how many dilations you need by matching the receptive field (of the TCN) with the sequences' lengths.
nb_stacks: Not very useful unless your sequences are very long (like waveforms with hundreds of thousands of time steps).
padding: I have only used causal since a TCN stands for Temporal Convolutional Networks. Causal prevents information leakage.
use_skip_connections: Skip connections connects layers, similarly to DenseNet. It helps the gradients flow. Unless you experience a drop in performance, you should always activate it.
return_sequences: Same as the one present in the LSTM layer. Refer to the Keras doc for this parameter.
dropout_rate: Similar to recurrent_dropout for the LSTM layer. I usually don't use it much. Or set it to a low value like 0.05.
activation: Leave it to default. I have never changed it.
kernel_initializer: If the training of the TCN gets stuck, it might be worth changing this parameter. For example: glorot_uniform.
use_batch_norm, use_weight_norm, use_weight_norm: Use normalization if your network is big enough and the task contains enough data. I usually prefer using use_layer_norm, but you can try them all and see which one works the best.

Receptive field

This formula is the one that works with the TensorFlow/Keras implementation. The receptive field can be calculated using the following formula:

where N_s is the number of stacks, N_b is the number of residual blocks per stack, d is a vector containing the dilations of each residual block in each stack, and K is the kernel size.

In theory, the 2 is not justified. We are still not sure why in practice we need to add this 2 in the formula. It would be appreciated if someone could point out why. It is a probably a parameterization/notation problem. There is a beginning of answer here.

If a TCN has only one stack of residual blocks with a kernel size of 2 and dilations [1, 2, 4, 8], its receptive field is 16. The image below illustrates it:

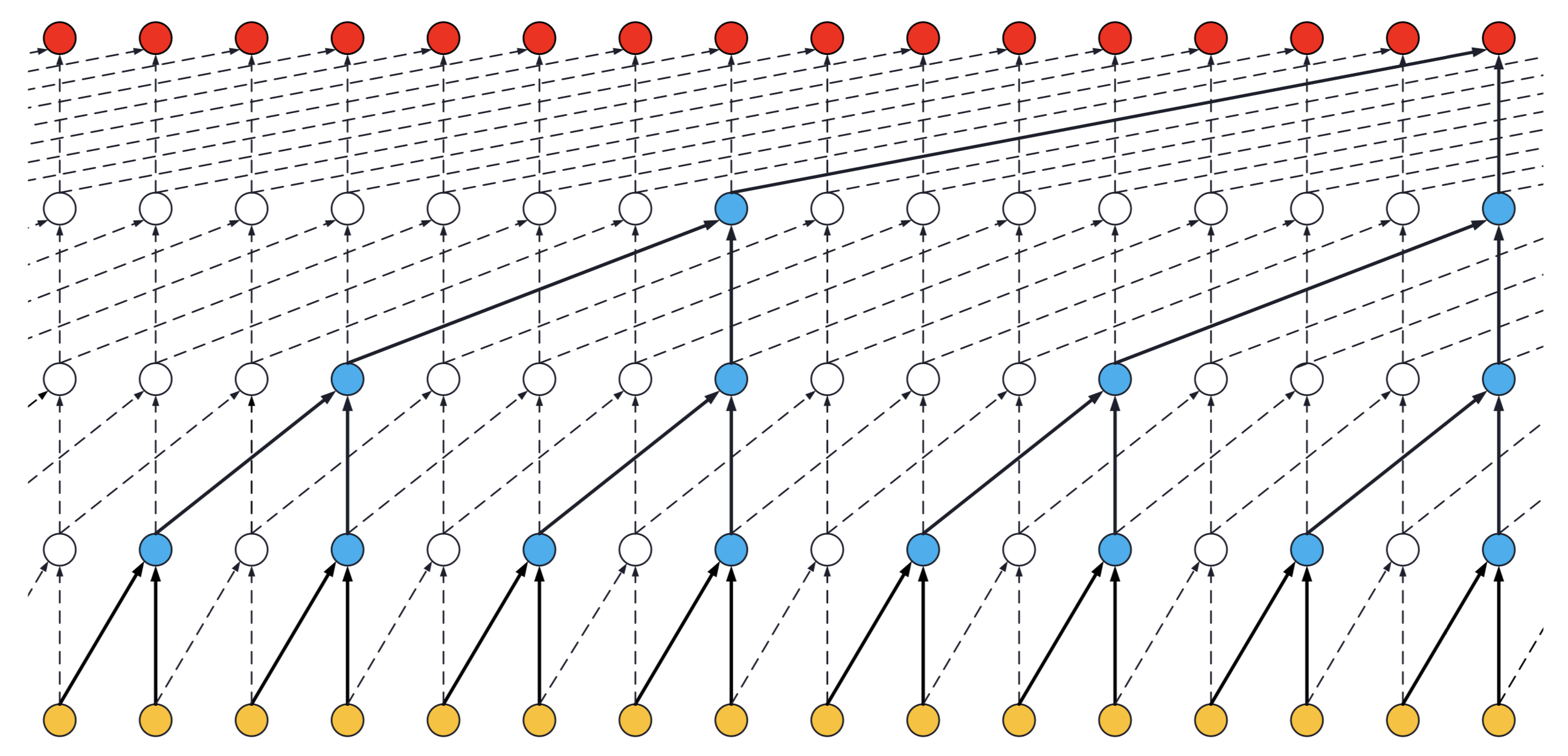ks = 2, dilations = [1, 2, 4, 8], 1 block

If the TCN has now 2 stacks of residual blocks, you would get the situation below, that is, an increase in the receptive field up to 31:

ks = 2, dilations = [1, 2, 4, 8], 2 blocks

If we increased the number of stacks to 3, the size of the receptive field would increase again, such as below:

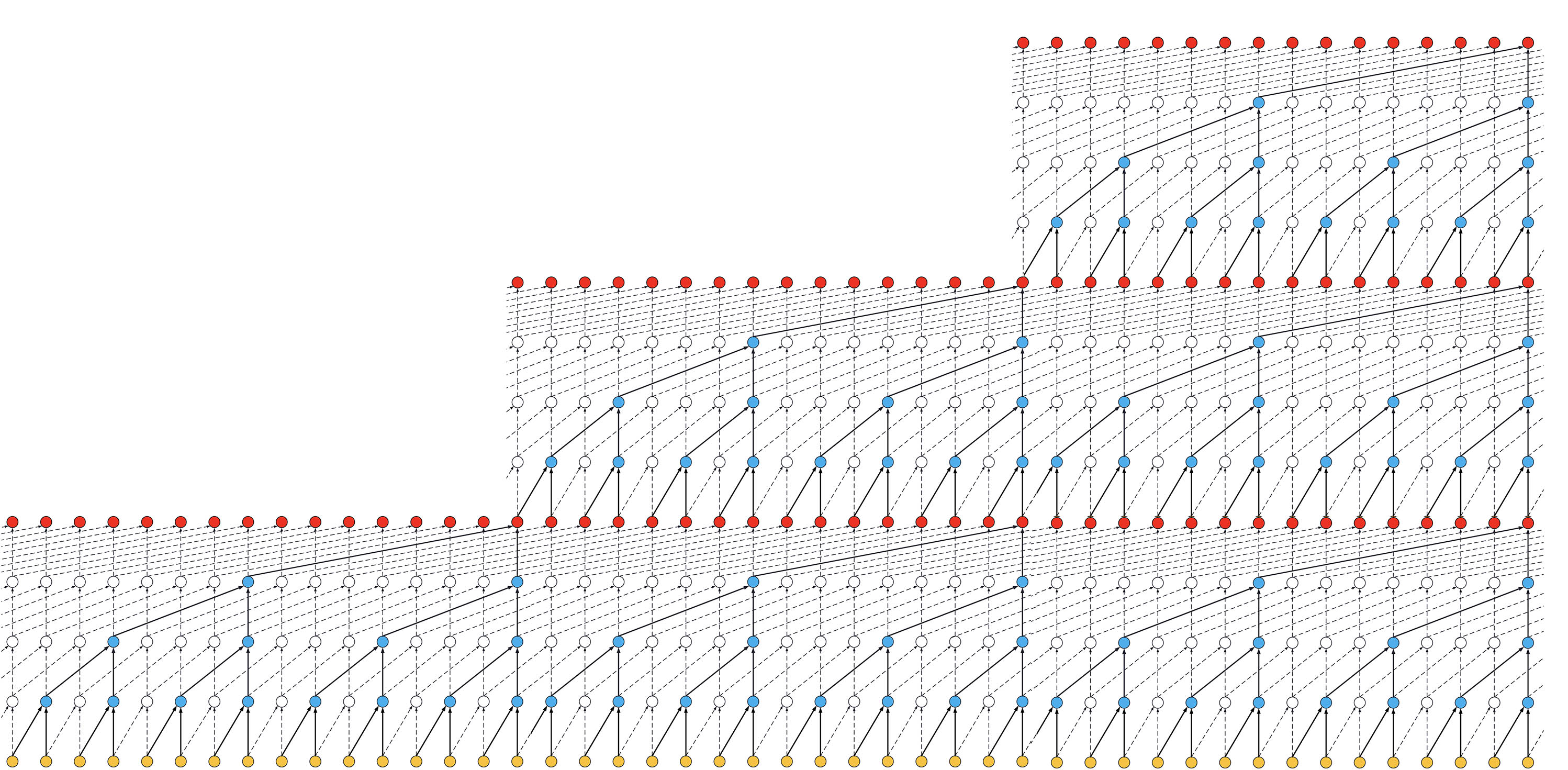ks = 2, dilations = [1, 2, 4, 8], 3 blocks

Non-causal TCN

Making the TCN architecture non-causal allows it to take the future into consideration to do its prediction as shown in the figure below.

However, it is not anymore suitable for real-time applications.

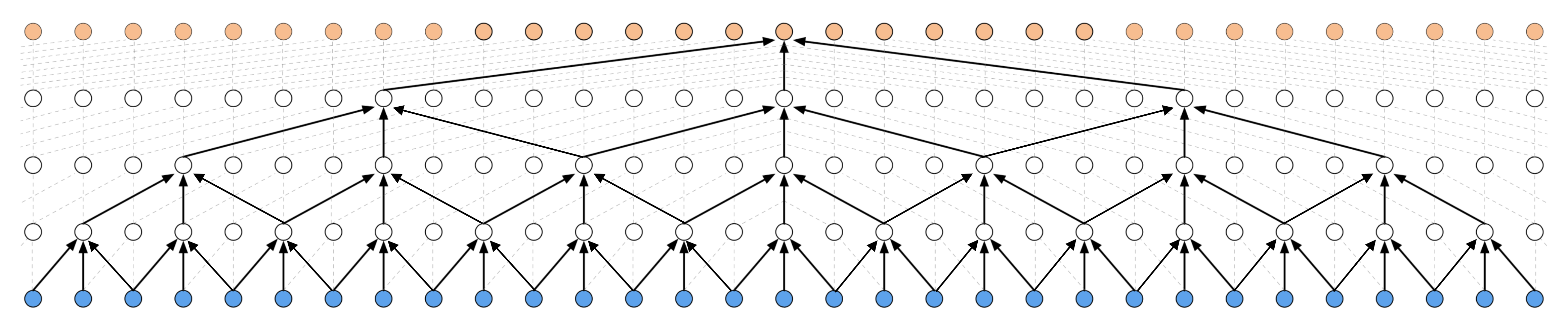Non-Causal TCN - ks = 3, dilations = [1, 2, 4, 8], 1 block

To use a non-causal TCN, specify padding='valid' or padding='same' when initializing the TCN layers.

Installation from the sources

git clone git@github.com:philipperemy/keras-tcn.git && cd keras-tcn
virtualenv -p python3 venv
source venv/bin/activate
pip install -r requirements.txt
pip install .

Run

Once keras-tcn is installed as a package, you can take a glimpse of what is possible to do with TCNs. Some tasks examples are available in the repository for this purpose:

cd adding_problem/
python main.py # run adding problem task

cd copy_memory/
python main.py # run copy memory task

cd mnist_pixel/
python main.py # run sequential mnist pixel task

Reproducible results

Reproducible results are possible on (NVIDIA) GPUs using the tensorflow-determinism library. It was tested with keras-tcn by @lingdoc and he got reproducible results.

Tasks

Word PTB

Language modeling remains one of the primary applications of recurrent networks. In this example, we show that TCN can beat LSTM without too much tuning. More here: WordPTB.

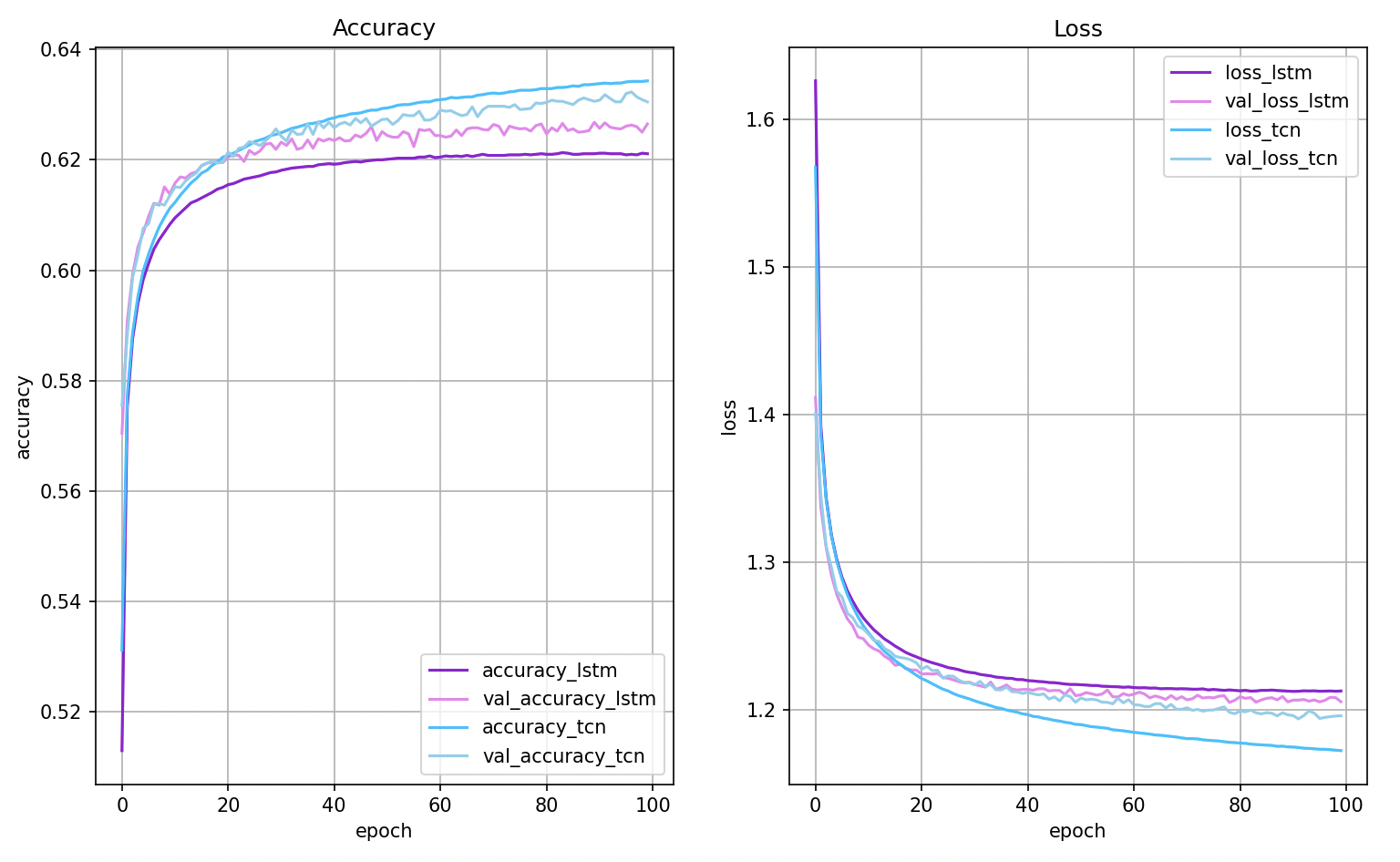
TCN vs LSTM (comparable number of weights)

Adding Task

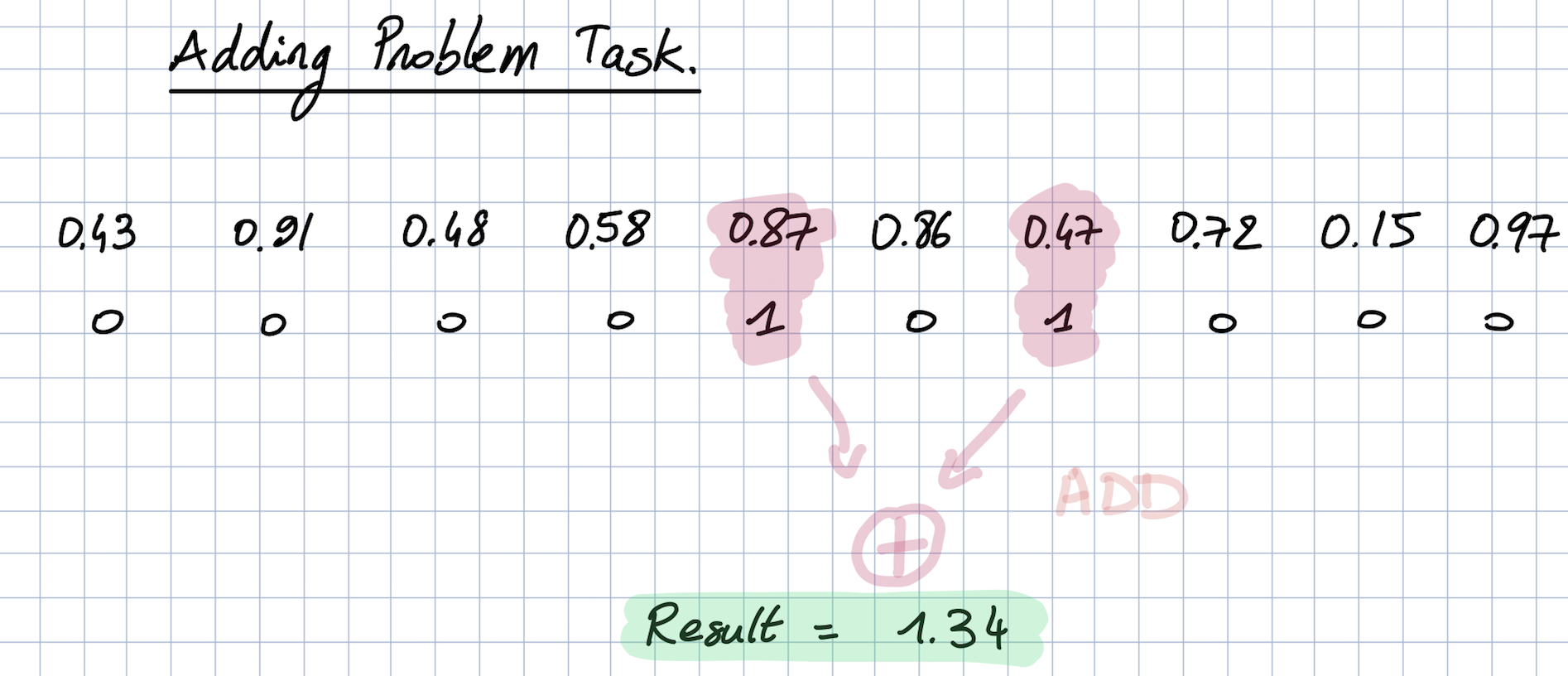
The task consists of feeding a large array of decimal numbers to the network, along with a boolean array of the same length. The objective is to sum the two decimals where the boolean array contain the two 1s.

Explanation

Adding Problem Task

Implementation results

782/782 [==============================] - 154s 197ms/step - loss: 0.8437 - val_loss: 0.1883
782/782 [==============================] - 154s 196ms/step - loss: 0.0702 - val_loss: 0.0111
[...]
782/782 [==============================] - 152s 194ms/step - loss: 6.9630e-04 - val_loss: 3.7180e-04

Copy Memory Task

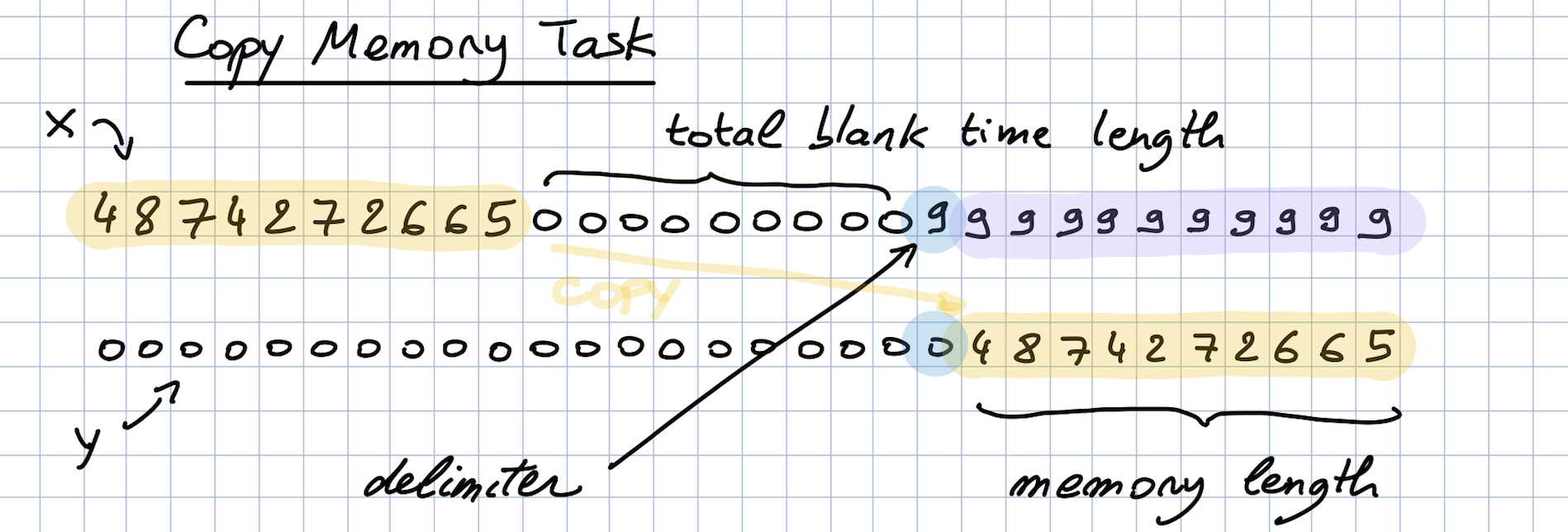
The copy memory consists of a very large array:

At the beginning, there's the vector x of length N. This is the vector to copy.
At the end, N+1 9s are present. The first 9 is seen as a delimiter.
In the middle, only 0s are there.

The idea is to copy the content of the vector x to the end of the large array. The task is made sufficiently complex by increasing the number of 0s in the middle.

Explanation

Copy Memory Task

Implementation results (first epochs)

118/118 [==============================] - 17s 143ms/step - loss: 1.1732 - accuracy: 0.6725 - val_loss: 0.1119 - val_accuracy: 0.9796
[...]
118/118 [==============================] - 15s 125ms/step - loss: 0.0268 - accuracy: 0.9885 - val_loss: 0.0206 - val_accuracy: 0.9908
118/118 [==============================] - 15s 125ms/step - loss: 0.0228 - accuracy: 0.9900 - val_loss: 0.0169 - val_accuracy: 0.9933

Sequential MNIST

Explanation

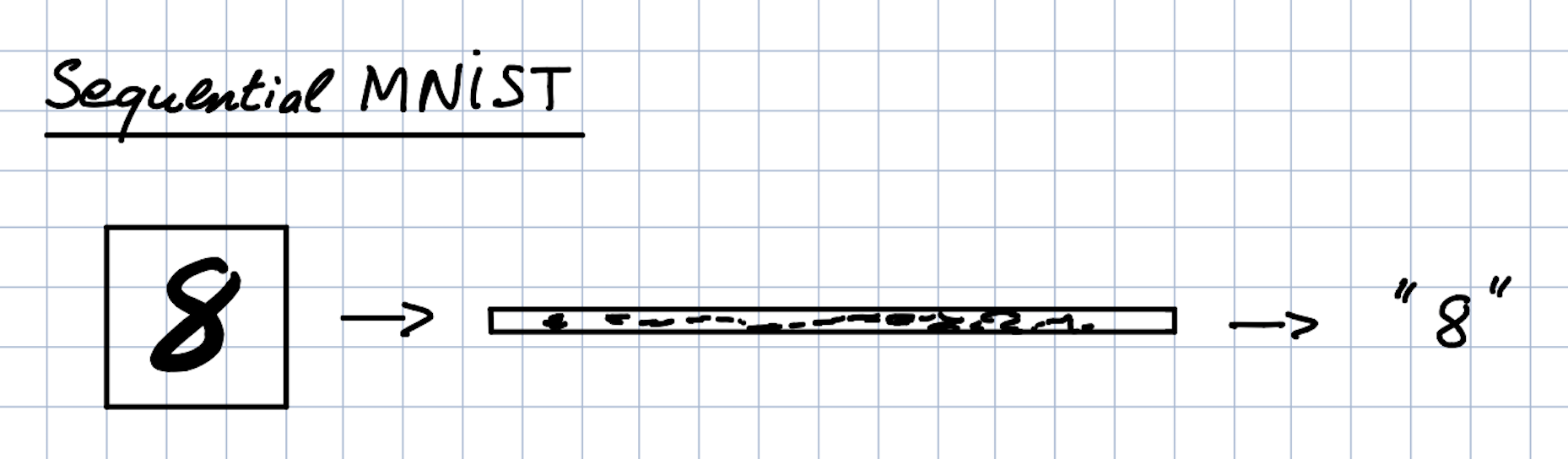
The idea here is to consider MNIST images as 1-D sequences and feed them to the network. This task is particularly hard because sequences are 28*28 = 784 elements. In order to classify correctly, the network has to remember all the sequence. Usual LSTM are unable to perform well on this task.

Sequential MNIST

Implementation results

1875/1875 [==============================] - 46s 25ms/step - loss: 0.0949 - accuracy: 0.9706 - val_loss: 0.0763 - val_accuracy: 0.9756
1875/1875 [==============================] - 46s 25ms/step - loss: 0.0831 - accuracy: 0.9743 - val_loss: 0.0656 - val_accuracy: 0.9807
[...]
1875/1875 [==============================] - 46s 25ms/step - loss: 0.0486 - accuracy: 0.9840 - val_loss: 0.0572 - val_accuracy: 0.9832
1875/1875 [==============================] - 46s 25ms/step - loss: 0.0453 - accuracy: 0.9858 - val_loss: 0.0424 - val_accuracy: 0.9862

Testing

Testing is based on Tox.

pip install tox
tox

References

https://github.com/locuslab/TCN/ (TCN for Pytorch)
https://arxiv.org/pdf/1803.01271 (An Empirical Evaluation of Generic Convolutional and Recurrent Networks for Sequence Modeling)
https://arxiv.org/pdf/1609.03499 (Original Wavenet paper)

https://github.com/Baichenjia/Tensorflow-TCN (Tensorflow Eager implementation of TCNs)

Citation

@misc{KerasTCN,
  author = {Philippe Remy},
  title = {Temporal Convolutional Networks for Keras},
  year = {2020},
  publisher = {GitHub},
  journal = {GitHub repository},
  howpublished = {\url{https://github.com/philipperemy/keras-tcn}},
}

Special thanks to:

@alextheseal
@qlemaire22

FreshWei/keras-tcn

Keras TCN

Why Temporal Convolutional Network instead of LSTM/GRU?

Index

API

Arguments

Input shape

Output shape

How do I choose the correct set of parameters to configure my TCN layer?

Receptive field

Non-causal TCN

Installation from the sources

Run

Reproducible results

Tasks

Word PTB

Adding Task

Explanation

Implementation results

Copy Memory Task

Explanation

Implementation results (first epochs)

Sequential MNIST

Explanation

Implementation results

Testing

References

Related

Citation