GBERESEARCH/optionvisualizer

Visualize option prices and sensitivities

optionvisualizer

Visualize option prices and sensitivities

 

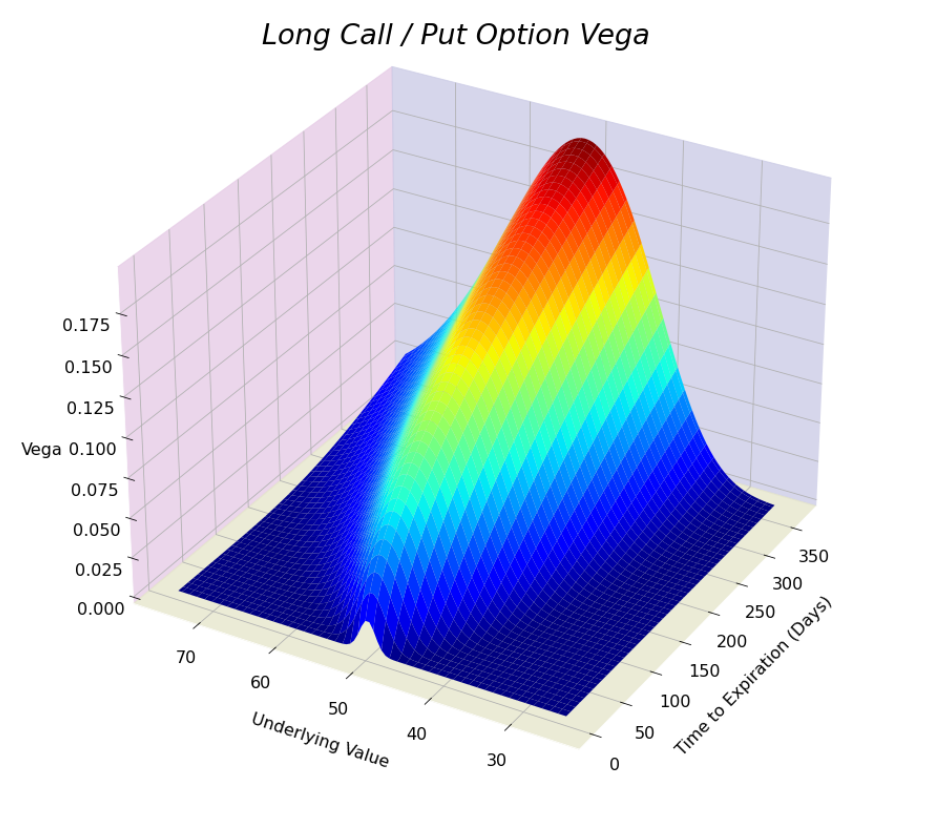
Each of the functions comes with default parameters and can be run without arguments for ease of illustration or they can be specified individually. Sensitivities can be calculated both analytically and numerically.

 

Installation

Install from PyPI:

$ pip install optionvisualizer

 

Install in a new environment using Python venv:

Create base environment of Python 3.11

$ py -3.11 -m venv .venv

Activate new environment

$ .venv\scripts\activate

Ensure pip is up to date

$ (.venv) python -m pip install --upgrade pip

Install Spyder

$ (.venv) python -m pip install spyder

Install package

$ (.venv) python -m pip install optionvisualizer

 

Or to install in new environment using anaconda:

$ conda create --name optvis

Activate new environment

$ activate optvis

Install Python

(optvis) $ conda install python==3.9

Install Spyder

(optvis) $ conda install spyder

Install package

(optvis) $ pip install optionvisualizer

 

Setup

Import visualizer and initialise an Option object

from optionvisualizer.visualizer import Visualizer
opt = Visualizer()

 

Black-Scholes option pricing and sensitivities:

• Price: option price
• Delta: sensitivity of option price to changes in asset price
• Gamma: sensitivity of delta to changes in asset price
• Vega: sensitivity of option price to changes in volatility
• Theta: sensitivity of option price to changes in time to maturity
• Rho: sensitivity of option price to changes in the risk free rate
• Vomma: sensitivity of vega to changes in volatility; Volga
• Vanna: sensitivity of delta to changes in volatility / of vega to changes in asset price
• Charm: sensitivity of delta to changes in time to maturity aka Delta Bleed
• Zomma: sensitivity of gamma to changes in volatility
• Speed: sensitivity of gamma to changes in asset price; 3rd derivative of option price wrt spot
• Color: sensitivity of gamma to changes in time to maturity; GammaTheta
• Ultima: sensitivity of vomma to changes in volatility; 3rd derivative of option price wrt volatility
• Vega Bleed: sensitivity of vega to changes in time to maturity

opt.option_data(option_value='price', S=3477, K=3400, T=0.5, r=0.005, q=0, sigma=0.3, option='put')

opt.sensitivities(greek='delta', S=3477, K=3400, T=0.5, r=0.005, q=0, sigma=0.3, option='put')

 

2D greeks graphs:

Charts of 3 options showing price, vol or time against:

• option value
• delta
• gamma
• vega
• theta

 

Long Call Delta vs Price

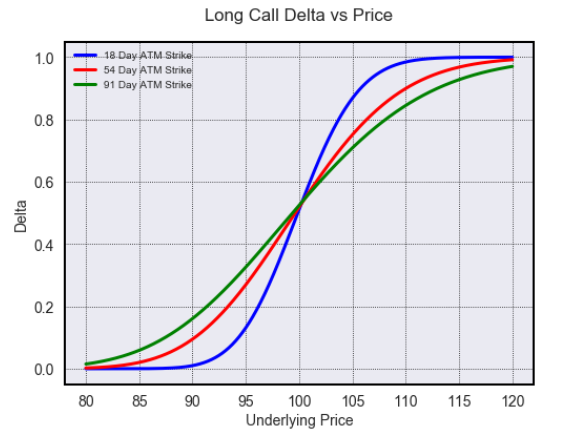
opt.visualize(risk=True, x_plot='price', y_plot='delta', G1=100, G2=100, G3=100, T1=0.05, T2=0.15, T3=0.25)

 

Long Call Theta vs Price

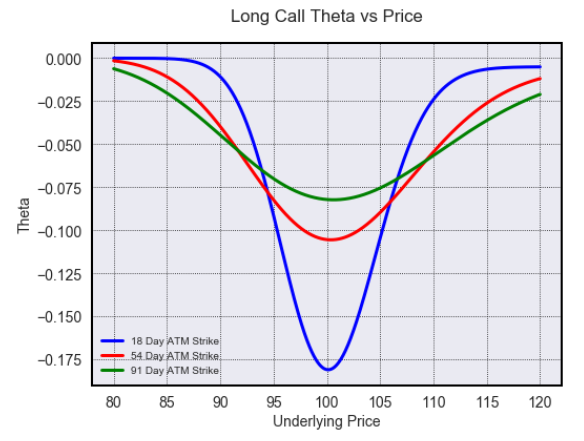
opt.visualize(risk=True, x_plot='price', y_plot='theta', G1=100, G2=100, G3=100, T1=0.05, T2=0.15, T3=0.25)

 

Charts of 4 options showing price, strike and vol against rho

Short Rho vs Strike

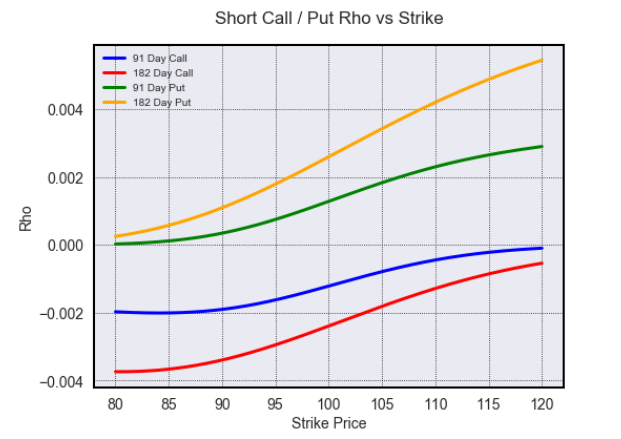
opt.visualize(risk=True, x_plot='strike', y_plot='rho', direction='short')

 

You can also convert into an animated gif

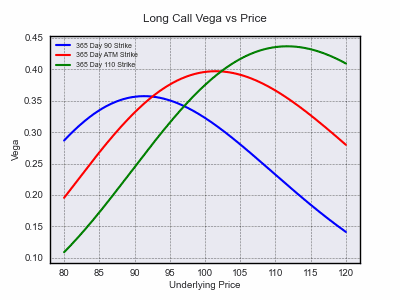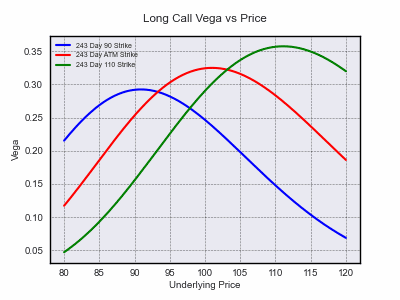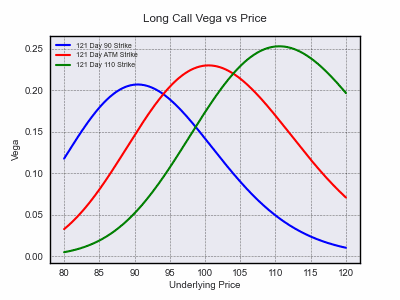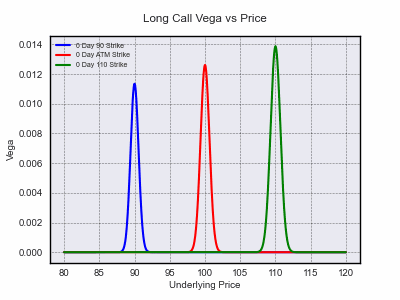
opt.animated_gif(graphtype='2D', x_plot='price', y_plot='vega', direction='long', T=1, gif_folder='images/greeks_2d', gif_filename='price_vega_l')

 

3D greeks graphs:

Each of the greeks above can be plotted showing Time to Expiration against Strike or Volatility

 

Using matplotlib:

Long Vega

opt.visualize(risk=True, graphtype='3D', greek='vega', S=50)

 

Short Gamma

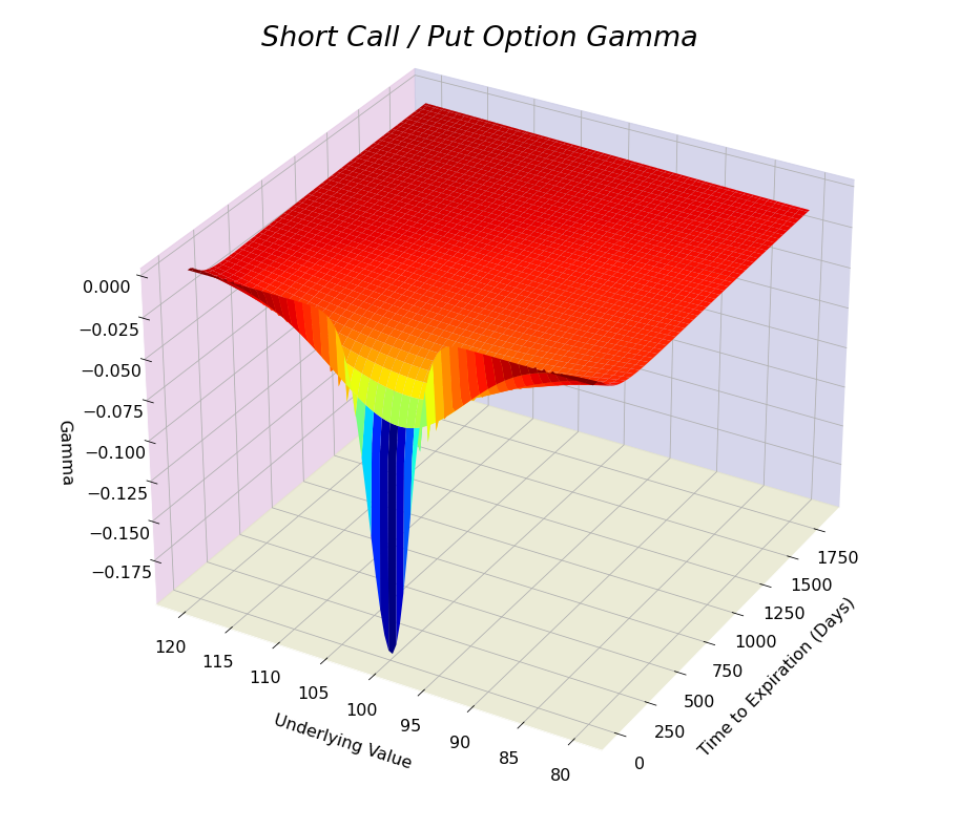
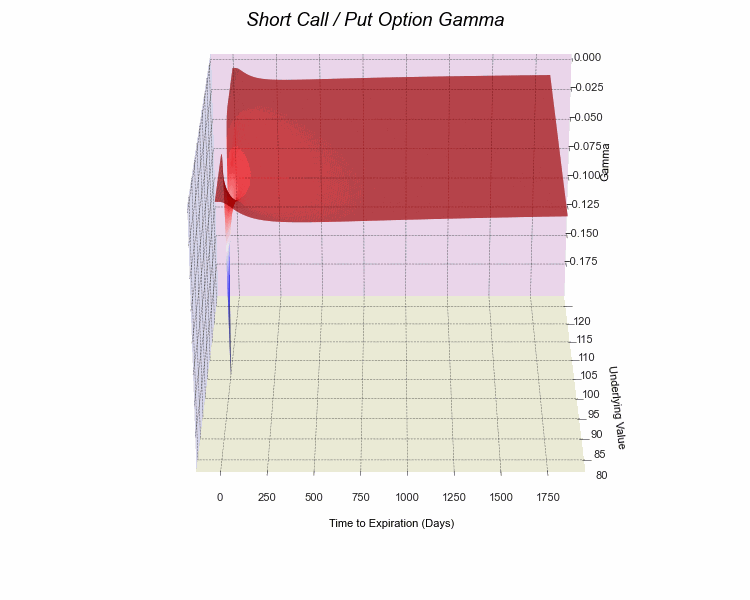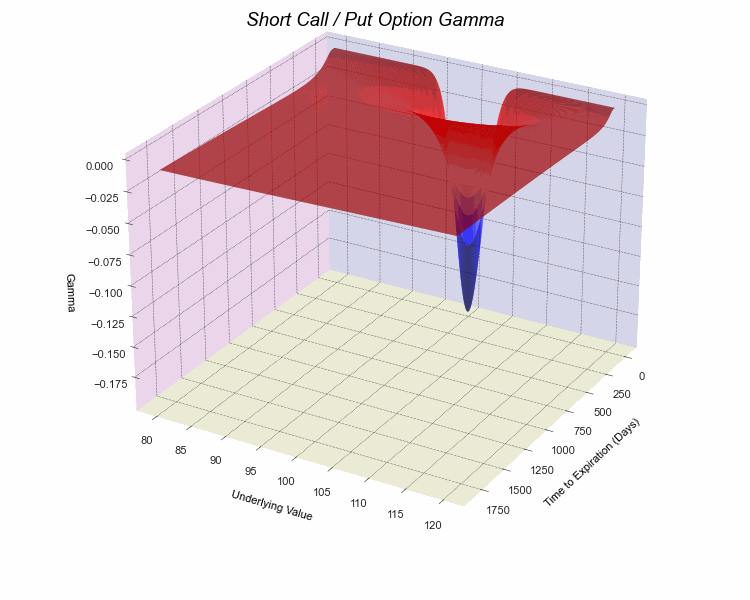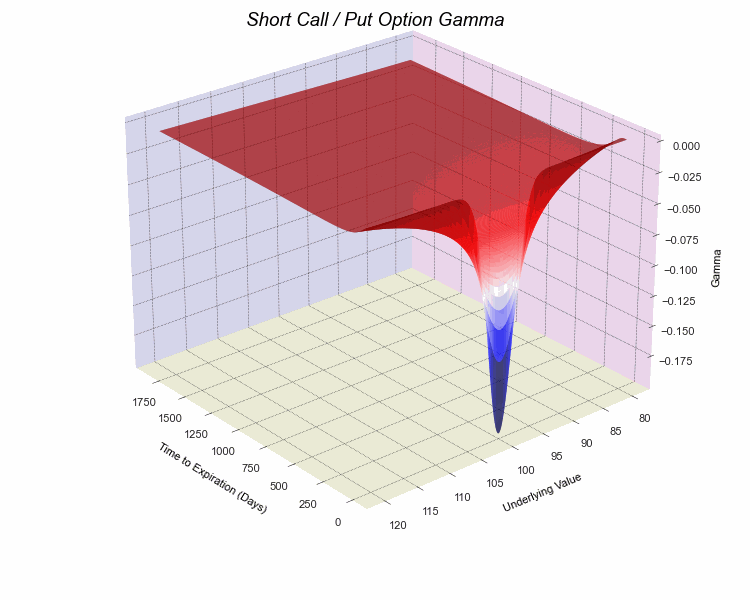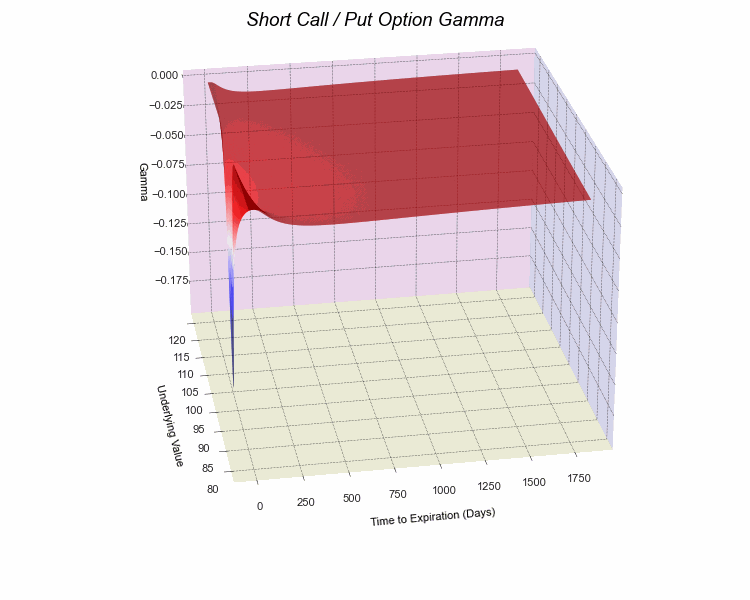
opt.visualize(risk=True, graphtype='3D', greek='gamma', direction='short')

 

Or using plotly display a graph that can be rotated and zoomed:

Long Call Price

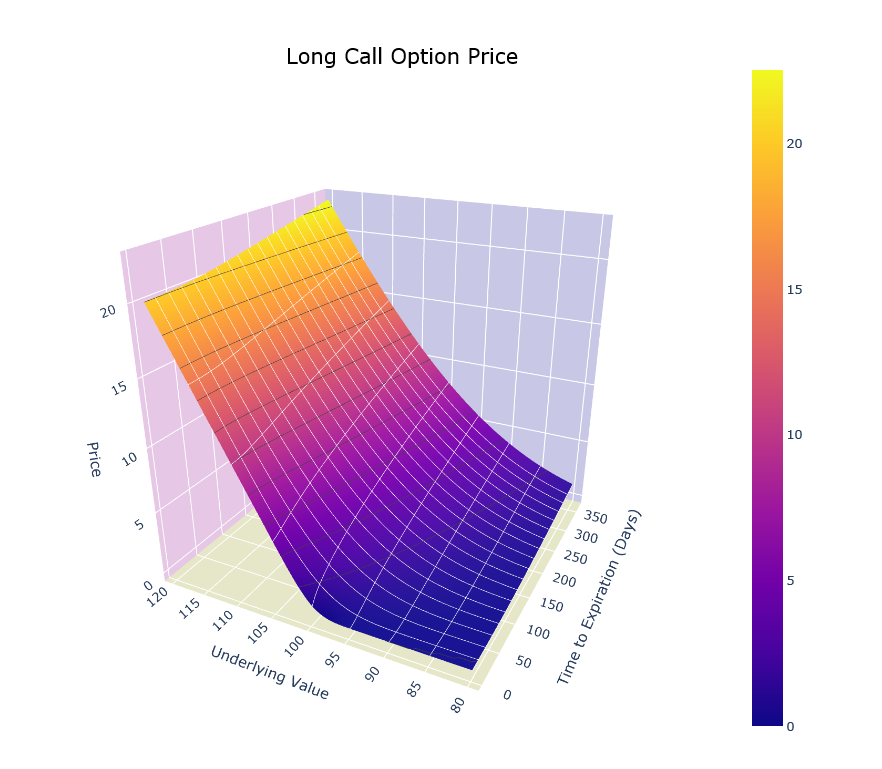
opt.visualize(risk=True, graphtype='3D', greek='price', colorscheme='Plasma', interactive=True)

 

Long Put Price against Volatility

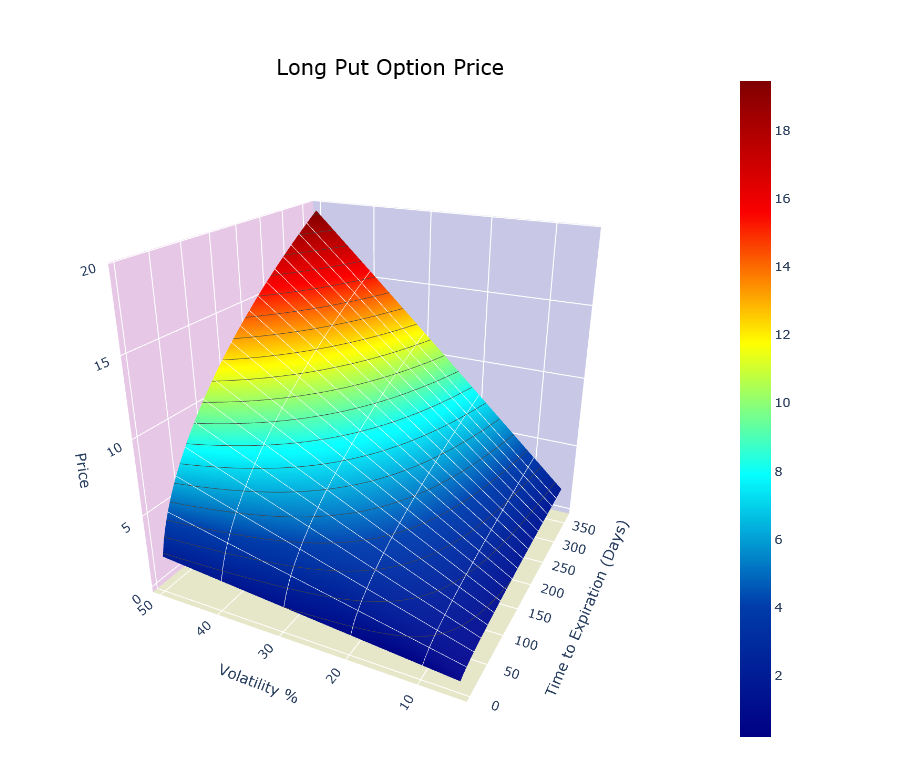
opt.visualize(risk=True, graphtype='3D', greek='price', axis='vol', option='put', interactive=True) 

 

Long Vanna

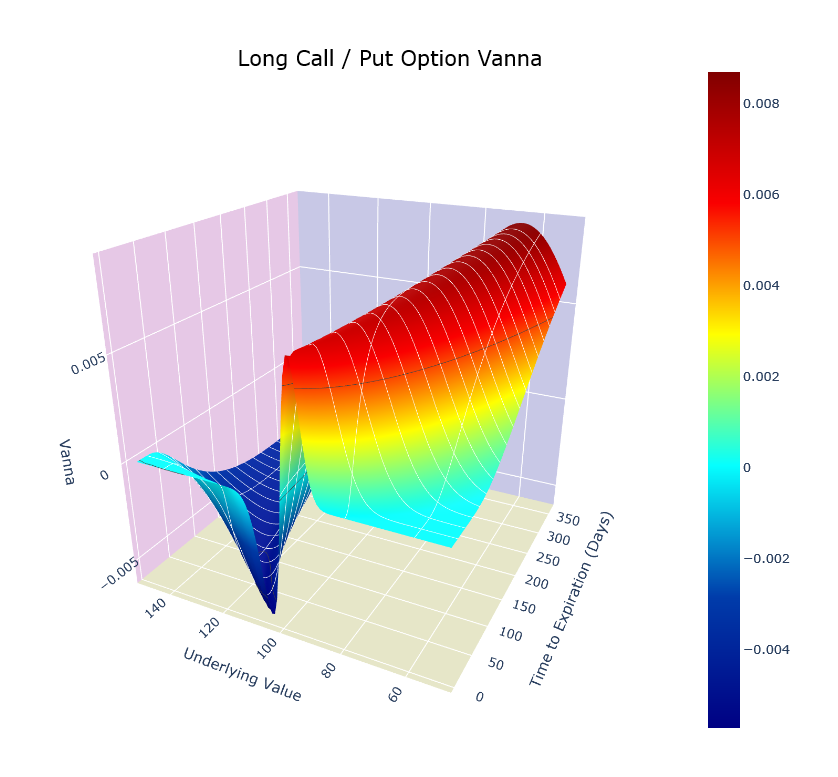
opt.visualize(risk=True, graphtype='3D', greek='vanna', sigma=0.4, interactive=True)

 

Short Zomma

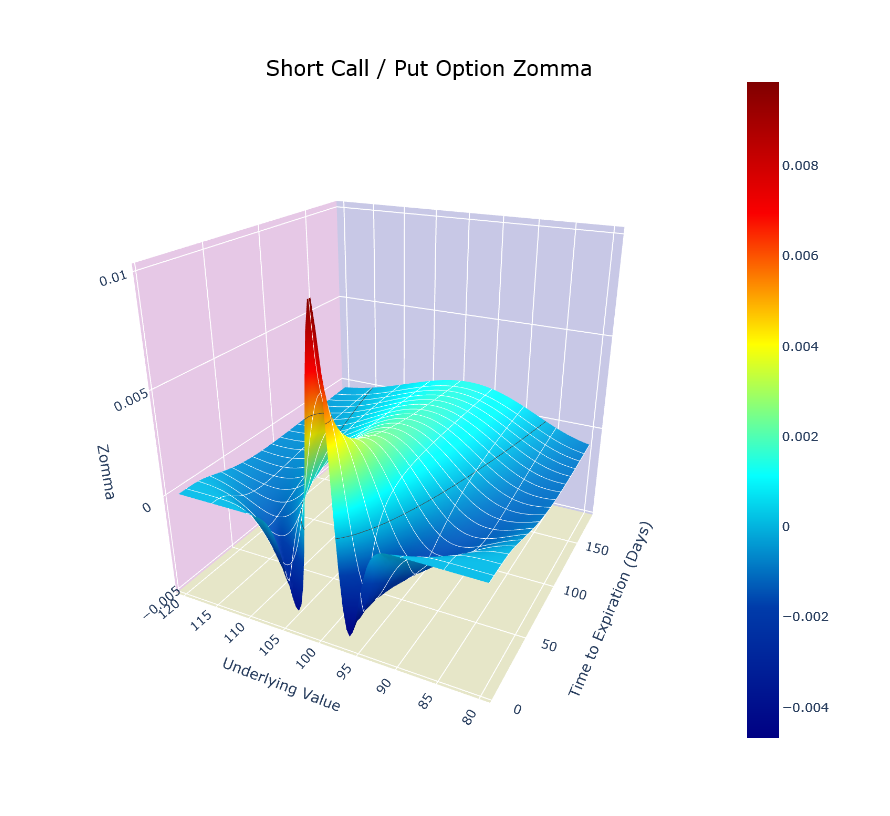
opt.visualize(risk=True, graphtype='3D', greek='zomma', direction='short', interactive=True)

 

You can also convert into an animated gif

opt.animated_gif(graphtype='3D', greek='gamma', direction='short', gif_folder='images/greeks_3d',gif_filename='gamma_s', gif_min_dist=9.0, gif_max_dist=9.1, gif_min_elev=25, gif_max_elev=26, spacegrain=1000, colorscheme='seismic')

 

Option strategy Payoff graphs:

• call / put
• stock
• forward
• collar
• call / put spread
• backspread
• ratio vertical spread
• straddle
• strangle
• butterfly
• christmas tree
• iron butterfly
• iron condor

 

Short Call:

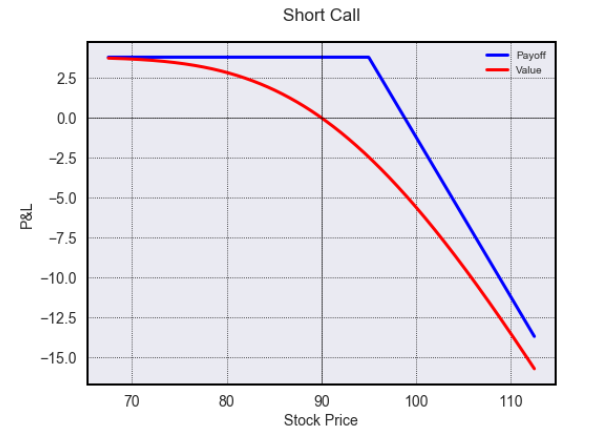
opt.visualize(risk=False, payoff_type='call', S=90, K=95, T=0.75, r=0.05, q=0, sigma=0.3, direction='short', value=True)

 

Long Straddle:

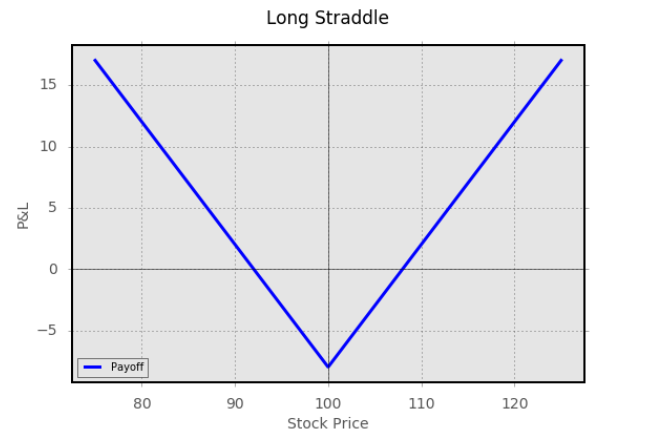
opt.visualize(risk=False, payoff_type='straddle', mpl_style='ggplot')

 

Short Christmas Tree:

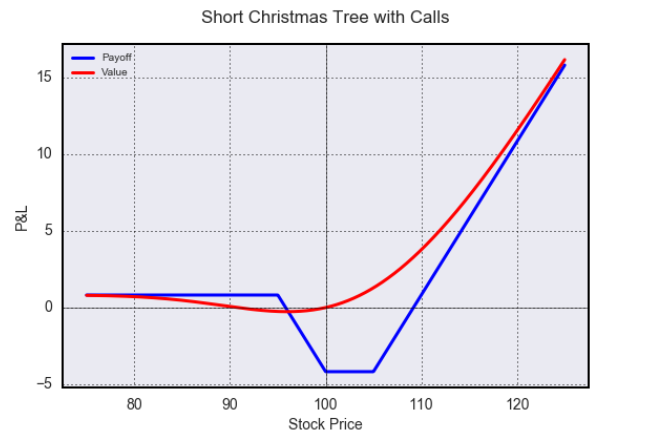
opt.visualize(risk=False, payoff_type='christmas tree', value=True, direction='short')

 

The following volumes served as a reference for the formulas and charts:

• The Complete Guide to Option Pricing Formulas, 2nd Ed, E. G. Haug
• Option Volatility & Pricing, S. Natenburg