Stable Fluid Simulation

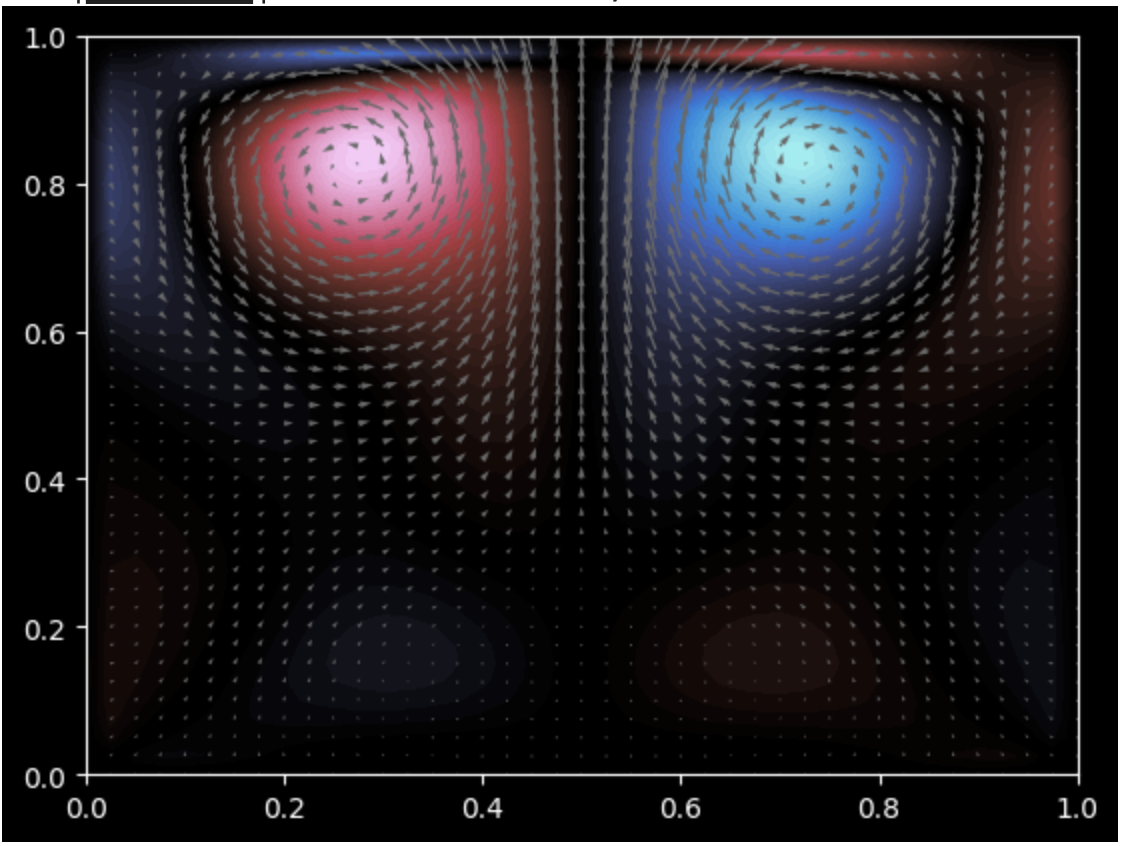
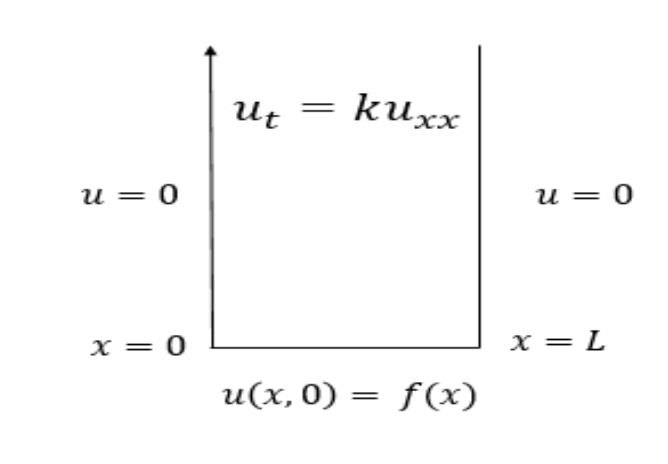Solution to the Incompressible Navier Stokes equations using "Stable Fluids" method proposed by Jos Stam in a closed box with a forcing function that creates a bloom.

Method

Section describes the equations and method used to write up the simulation.

basic equations

The solution is based off Navier Stokes Equation particularly:

$$\frac{\partial u}{\partial t} + (u \cdot \nabla)u = \frac{-1}{\rho} \cdot \nabla p + \nu \cdot \nabla^{2}u + f $$

Incompressibility Equation in the simulation is based on:

$$\nabla \cdot u = 0 $$

where:

u: Velocity (assumed to be a 2D vector)
p: pressure
f: Forcing
$\rho$: Density
$\nu$: Kinematic Viscosity
t: Time
$\nabla$: Nonlinear Convection as well as divergence and gradient
$\nabla^{2}$: Laplace Operator

The box will start the simulation as a Homogenuous Dirichlet Boundary Condition as seen below :

The forcing function, is an upwards force in the lower center of the domain (ie., relative to the box above).

solution

The simulation starts with zero velocity across the entire grid, so $u$ will be set as $u=[0, 0]$.
The sim then adds forces through euler stepping (only one in our sim):

$$w_{1} = u + \Delta t \cdot f$$

Convection is done through self-advection. It is essentially a process of setting the value at the current location to be the balue at the position previously (i.e., backtracked) on the streamline placed.

$$w_{2} = w_{1}(p(x, -\Delta t)) $$

We then diffuse implicitly by solving a linear system matrix-free. This is done by using Conjugate Gradient, which may be unconditionally stable, but works for the stake of sim:

$$ (I - \nu \cdot \Delta t \cdot \nabla^{2})\cdot w_{3} = w_{2}$$

This step is realtively straightforward, but is broken down into multiple steps:

a) The simulation starts this step off by computing a pressure correction by solving a linear system matrix-free also with a Conjugate Gradient and the use of Poisson Operator:

$$\nabla^{2} \cdot p = \nabla \cdot w_{3}$$

b) The velocities then get corrected to be incompressible:

$$w_{4} = w_{3} - \nabla p$$

The simulation advances to the next iteration of the solution by updating $u$ to:

$$u=w_{4}$$

things to consider

a) The simulation only does one Euler-Step which can lead to inaccuracies and instability. May require multiple Euler-Steps that include backtracking multiple steps .

b) All parameters can be chosen arbitrarily. And thus, the simulation is unstable because the advection may not work correctly depending on the values you give it. This goes back to the fact that self-advection may backtrack to a places that may be unusual or even worse, outside the grid.

c) To view the timestamps of the simulation, view StableFluid.ipynb on the last cell. 100 iterations have been of the simulation modelling behaviour over time.

Inspiration