Regularized Autoencoders for Isometric Representation Learning

The official repository for <Regularized Autoencoders for Isometric Representation Learning> (Lee, Yoon, Son, and Park, ICLR 2022).

This paper proposes Isometrically Regularized Variational Autoencoders (IRVAE), a regularized autoencoder trained by minimizing the VAE loss function + relaxed distortion measure. It produces isometric representation where Euclidean distances approximate geodesic distances in the learned manifold.

Coordinate-Invariant Relaxed Distortion Measure

def relaxed_distortion_measure(func, z, eta=0.2, create_graph=True):
    '''
    func: decoder that maps "latent value z" to "data", where z.size() == (batch_size, latent_dim)
    '''
    bs = len(z)
    z_perm = z[torch.randperm(bs)]
    alpha = (torch.rand(bs) * (1 + 2*eta) - eta).unsqueeze(1).to(z)
    z_augmented = alpha*z + (1-alpha)*z_perm
    v = torch.randn(z.size()).to(z)
    Jv = torch.autograd.functional.jvp(
        func, z_augmented, v=v, create_graph=create_graph)[1]
    TrG = torch.sum(Jv.view(bs, -1)**2, dim=1).mean()
    JTJv = (torch.autograd.functional.vjp(
        func, z_augmented, v=Jv, create_graph=create_graph)[1]).view(bs, -1)
    TrG2 = torch.sum(JTJv**2, dim=1).mean()
    return TrG2/TrG**2

To implement the relaxed distortion measure for your decoder or generator function, you can simply copy and paste the above code block.

Preview (MNIST)

1. MNIST images of digits 0 and 1

Figure 1: (Left) Distorted Representation obtained by VAE, (Middle) Isometric Representation obtained by IRVAE, and (Right) Isometric Embedding obtained by Isomap (non-parametric manifold learning approach). Ellipses represent pullbacked Riemannian metrics; the more isotropic and homogeneous, the more isometric.

2. MNIST images of digits 0, 1, and 5

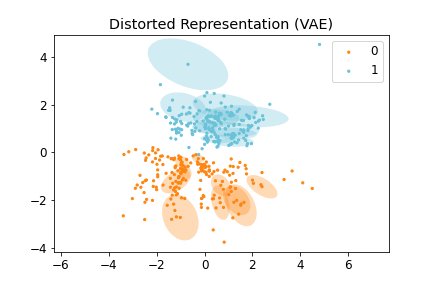
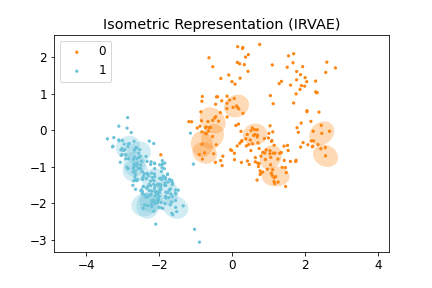
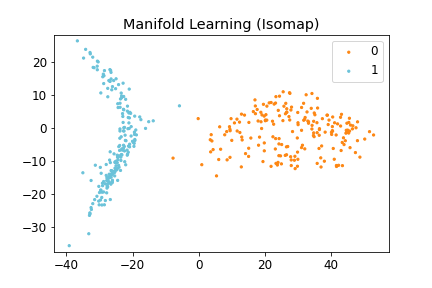
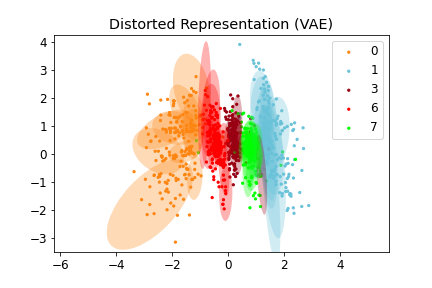
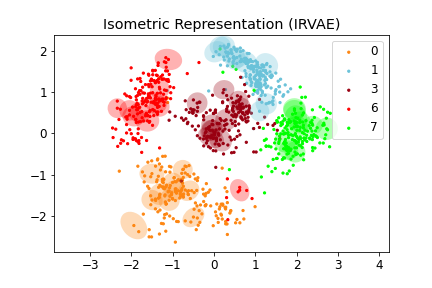
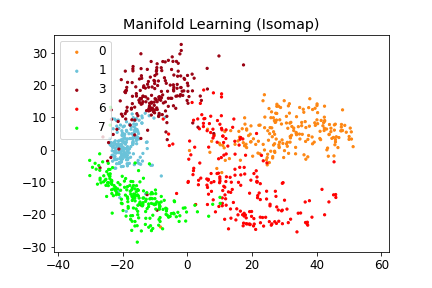
Figure 2: (Left) Distorted Representation obtained by VAE, (Middle) Isometric Representation obtained by IRVAE, and (Right) Isometric Embedding obtained by Isomap (non-parametric manifold learning approach). Ellipses represent pullbacked Riemannian metrics; the more isotropic and homogeneous, the more isometric.

3. MNIST images of digits 0, 1, 3, 6, and 7

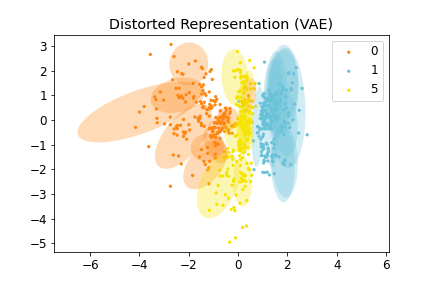
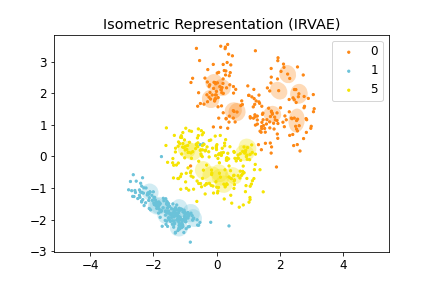
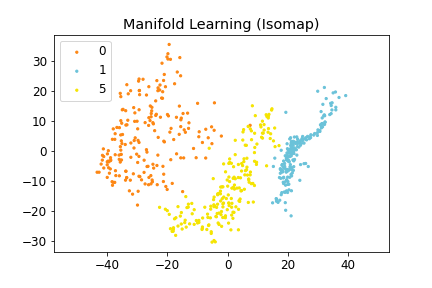
Figure 3-1: (Left) Distorted Representation obtained by VAE, (Middle) Isometric Representation obtained by IRVAE, and (Right) Isometric Embedding obtained by Isomap (non-parametric manifold learning approach). Ellipses represent pullbacked Riemannian metrics; the more isotropic and homogeneous, the more isometric.

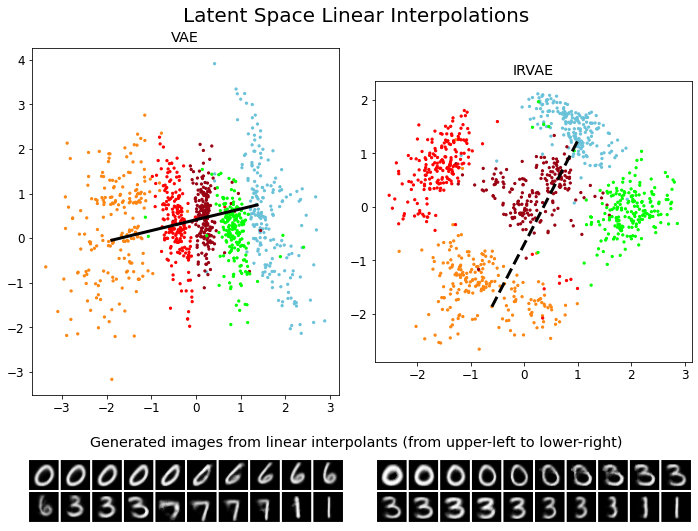
Figure 3-2: Latent Space Linear Interpolations and Generated Images in VAE and IRVAE.

Environment

The project is developed under a standard PyTorch environment.

python 3.8.8
numpy
matplotlib
argparse
yaml
omegaconf
torch 1.8.0
CUDA 11.1
tensorboard

Running

1. Train

1.1 VAE

python train.py --config configs/mnist_vae_z2.yml --run vae_mnist_{digits} --data.training.digits list_{digits} --data.validation.digits list_{digits} --device 0

1.2 IRVAE

python train.py --config configs/mnist_irvae_z2.yml --run irvae_mnist_{digits} --data.training.digits list_{digits} --data.validation.digits list_{digits} --model.iso_reg 1000 --device 0

If you want the training dataset to include MNIST digits 0, 1, and 2, you should set digits as 012. For example, digits can be 01, 015, or 24789.
The result will be saved in './results' directory.

2. Tensorboard

tensorboard --logdir results/

Scalars: loss/train_loss_ (training loss function), loss/val_loss_ (reconstruction error), iso_loss_ (isometric regularization term), MCN_ (mean condition number)
Images: input_ (input image), recon_ (reconstructed image), latent_space_ (latent space embeddings with equidistant ellipses)

3. Notebook

In 'notebook/1. MNIST_results.ipyng', you can find the figure generation code.

Citation

If you found this library useful in your research, please consider citing:

@inproceedings{
lee2022regularized,
title={Regularized Autoencoders for Isometric Representation Learning},
author={Yonghyeon Lee and Sangwoong Yoon and MinJun Son and Frank C. Park},
booktitle={International Conference on Learning Representations},
year={2022},
url={https://openreview.net/forum?id=mQxt8l7JL04}
}

Gabe-YHLee/IRVAE-public