该项目将Transform模型运用于时间序列数据预测 Transform流程直接上图, 为确保代码阅读的流畅性, 我将从数学原理上详细讲解transform模型, 以及项目的整个流程
处理数据依旧是二维结构化数据, 横向为特征, 纵向为时间(本文以一维数据为例, 模拟三角复合函数数据进行建模)
- 导入数据, 截取前80%的数据作为训练集, 后20%作为检验集, 之后预测后十期数据;
- 将数据转化为三维格式, tensor的维度为(N, timestep, feature_number), 其中N+timestep为样本容量(N为送入模型的样本容量,N+timestep为整个时序的样本容量), feature_number为样本的特征数(由于是一维时序数据, 所以特征数为1), 这样的三维tensor为xtrain,ytrain为xtrain的后几期数据,数据结构依旧是三维数据;
由于是时间序列数据,此处不需要作嵌入(embedding)处理,位置嵌入和词嵌入。
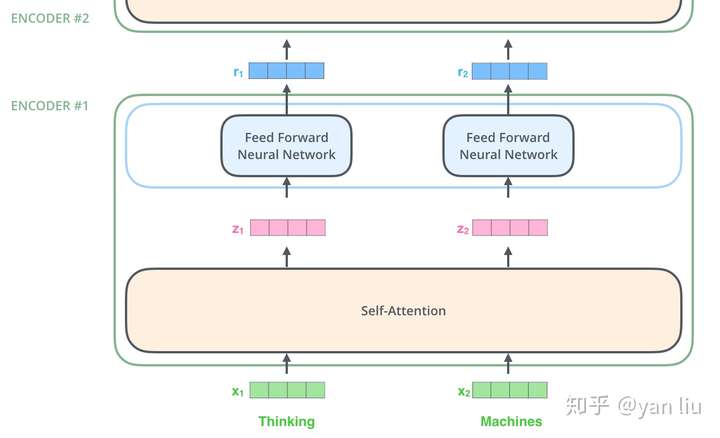
Attention机制本质是矩阵乘法,网上有很多很详细的教程,这里我简略提一下,Attention机制有两种, 一种为Self-Attention, 另一种为React-Attention:
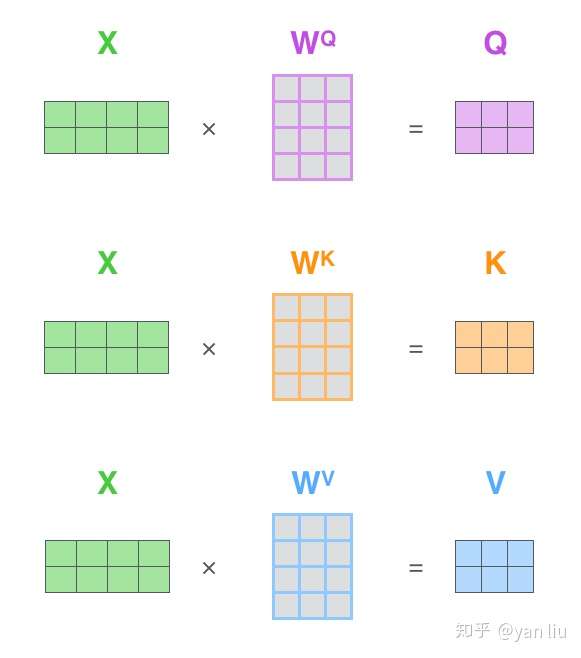
在自然语言处理的任务中送入模型的三维tensor的特征数一般不会为1,自然语言处理任务中的tensor维度可以理解为(文本数,文本中的词的个数, 词嵌入的维度), 我们以其中一个样本为例, 一个样本为二维矩阵, 初始化三个矩阵, 将样本矩阵与三个矩阵作乘法,得到Q、K、V矩阵:
Q矩阵乘以K的转置再对行作softmax运算,运算结果乘以V,最终得到一个注意力矩阵,这一运算过程即为Self-Attention的工作机制。这时会出现两个样本————即两个二维矩阵。初始化六个二维矩阵, 其中三个为其中一个文本矩阵提供Q、K、V矩阵,另外三个为另外一个文本矩阵提供Q、K、V矩阵,不妨记Q1、K1、V1、Q2、K2、V2,这时运算机制变成:Q1矩阵乘以K2的转置再对行作softmax运算,运算结果乘以V2,或者Q2矩阵乘以K1的转置再对行作softmax运算,运算结果乘以V1。
Mask机制一般作用在Self-Attention机制当中,更一般的,该机制作用条件要在行列相等的方阵中,在作softmax运算之前,将下三角元素全部替换成负无穷即可,后续运算保持不变。
多头机制, 对每个文本矩阵都取多个Q、K、V矩阵计算出的所有注意力矩阵横向拼接即为多头机制的运算机制。
本质为全连接网络,全连接网络的数量与timestep一致,不同timestep之间的全连接网络相互独立, 对于任意一个全连接网络而言,输入数据为(N, feature_number)的二维数据, 共有timestep个这种矩阵,在这一层当中,每个全连接网络是相互独立的。
在送入Attention以及Feed forward之前需要对数据做一次恒等映射, 缓解后续模型训练阶段梯度消失的问题:本质依旧是个全连接层, 输出结果与Attention或Feed forward的输出结果相加。
Transformer中的Normalization为layer级别的标准化, 与batch级别的标准化相对应,前者是对同一样本不同维度作标准化,后者是所有样本同一纬度的标准化。
输入数据维度为(N, timestep, feature), 输出维度为与输入维度类似,只是timestep可以任意指定, N和feature与输入数据一致,不妨记为(N, timestep2, feature), 模型的工作为,前timestep的数据去预测后timestep2个时间的数据。训练优化器多种多样,可以根据喜好来选择优化器, 建模见transformer.py、预测见predict.ipynb