君子博学而日参省乎己,则知明而行无过矣[1]。
PS: GitHub 的公式渲染不好影响阅读,所以特地将 markdown 文件生成了可供完美阅读的 pdf 格式。
目前用于训练神经网络的算法通常是基于梯度下降法进行误差反向传播[2],核心**是以目标函数的负梯度方向为搜索方向,通过每次迭代使待优化的目标函数逐步减小,最终使误差函数达到极小值。附加动量因子记忆上次迭代的变化方向[3],可以采用较大的学习速率系数以提高学习速度,但是参数调整优化过程依然线性收敛,相对速度依然较慢。
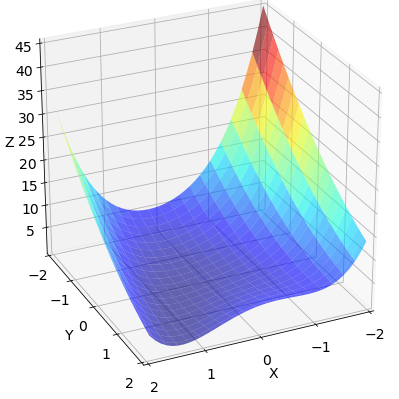
我们选取 Rosenbrock 函数 作为测试优化算法性能的函数,这是一个非凸函数,由公式 (1) 决定:
$$
\begin{align}
f(x,y)=(a-x)^{2}+b(y-x^{2})^{2} \tag{1}
\end{align}
$$
令
为了测试不同 learning rate 下梯度下降算法的表现,我们采用了 4 种优化策略:
- 固定学习率
$lr_{min}=0.001$ ;- 固定学习率
$lr_{max}=0.1$ ;- 固定学习率
$lr_{max}=0.1$ ,动量因子$\beta=0.1$ ;- 初始最大学习率
$lr_{max}=0.1$ ,每次迭代衰减为前次学习率的$0.9$ 倍,最终学习率不小于$lr_{min}=0.001$ 。
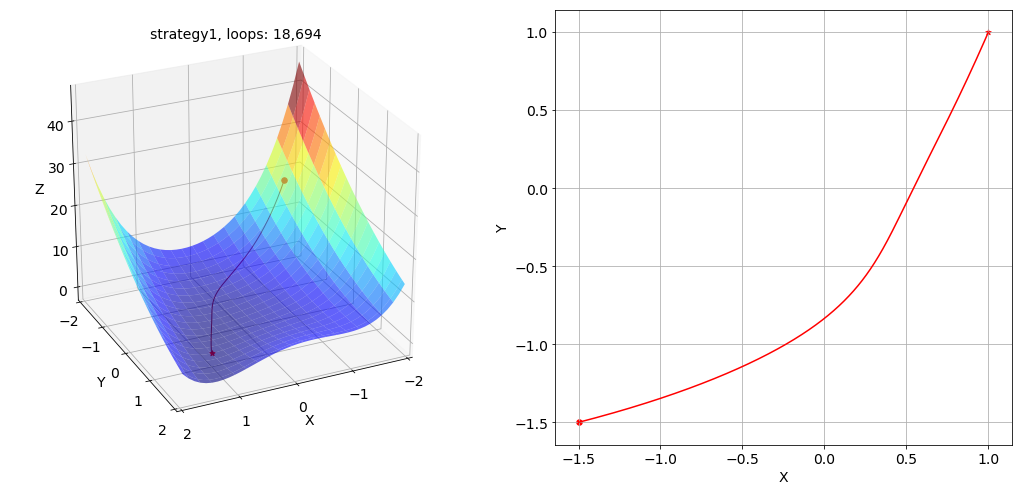
策略 1 下梯度下降法寻找最优解的路径及其在 x-y 平面投影的俯视图如下所示:
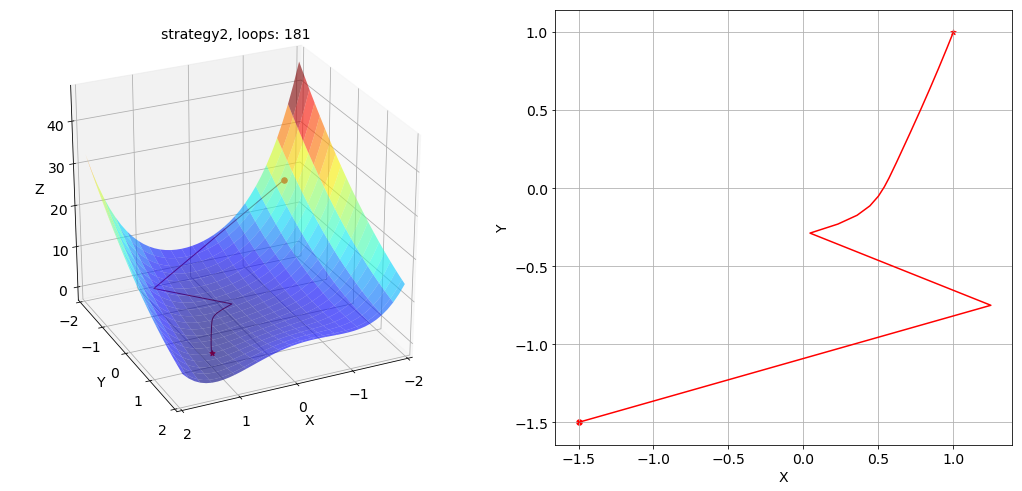
策略 2 下寻找最优解的路径及其在 x-y 平面投影的俯视图如下所示:
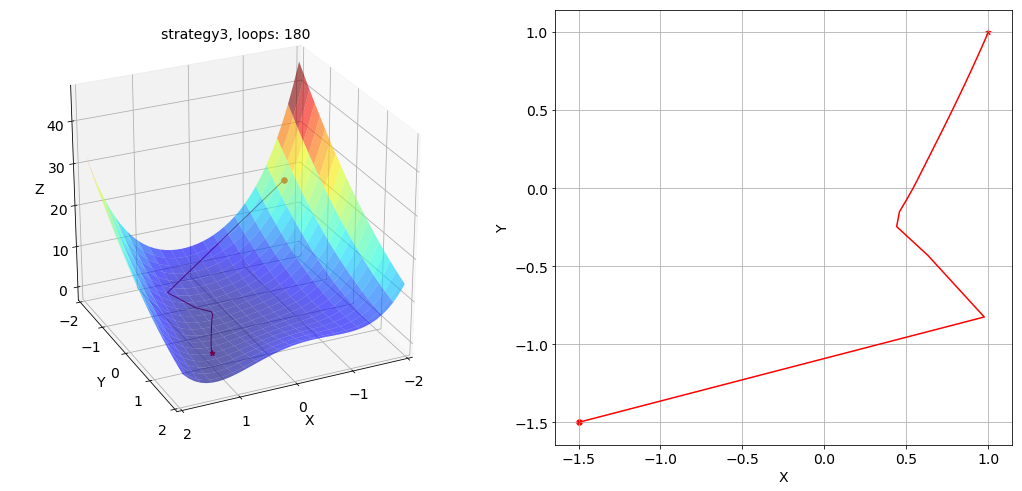
策略 3 下寻找最优解的路径及其在 x-y 平面投影的俯视图如下所示:
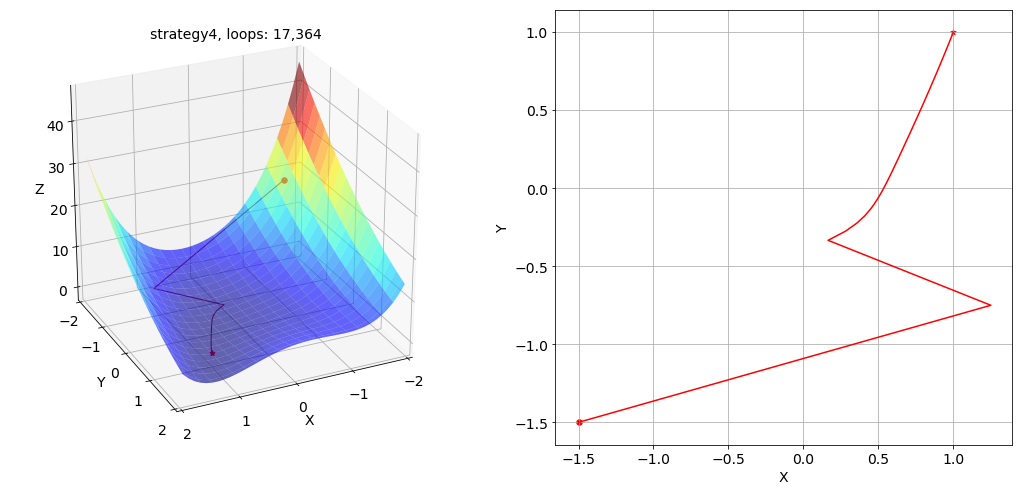
策略 4 下寻找最优解的路径及其在 x-y 平面投影的俯视图如下所示:
根据结果,明显可以看出学习率 learning rate 选择过小或过大会导致网络训练过慢或震荡发散,整个网络的训练速度对学习率的选取依赖程度很高。完整的代码及 jupyter notebook 文件已上传至该 repo 的 codes 和 notebooks 文件夹:
LM算法[4]是一种利用标准数值优化技术的快速算法,具有高斯牛顿法的局部收敛性和梯度下降法的全局特性,在局部搜索能力上强于梯度下降法。LM算法基本**是先沿着负梯度方向进行搜索,然后根据牛顿法在最优值附近产生一个新的理想的搜索方向。LM算法具有二阶收敛速度,迭代次数很少,可以大幅度提高收敛速度和算法的稳定性,避免陷入局部最小点的优点。
第 k+1 次迭代时模型的参数由
$$
\begin{align}
\mathbf{w}^{k+1}=\mathbf{w}^{k}+\Delta\mathbf{w}^{k} \tag{2}
\end{align}
$$
LM算法对模型参数的修正量
$$
\begin{align}
[\mathbf{J}^{T}(\mathbf{w})\mathbf{J}(\mathbf{w})-\mu \mathbf{I}]\Delta \mathbf{w}=-\mathbf{J^{T}}(\mathbf{w})\mathbf{e}(\mathbf{w}) \tag{3}
\end{align}
$$
其中,$\mathbf{J}(\mathbf{w})$ 为 Jacobian矩阵,$\mathbf{e}(\mathbf{w})$ 为期望值
$$
\begin{align}
\mathbf{e}(\mathbf{w})=\widehat{y}-y(\mathbf{w}) \tag{4}
\end{align}
$$
LM算法受参数
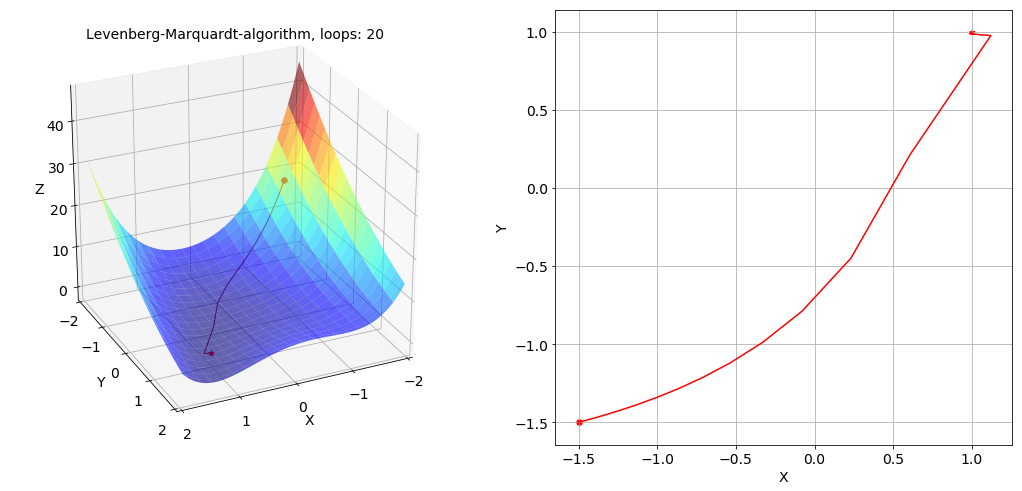
在实际使用的情况下,通常采取的策略是开始时使用较小的 x-y 平面投影的俯视图如下所示($\mu$ 的值固定为
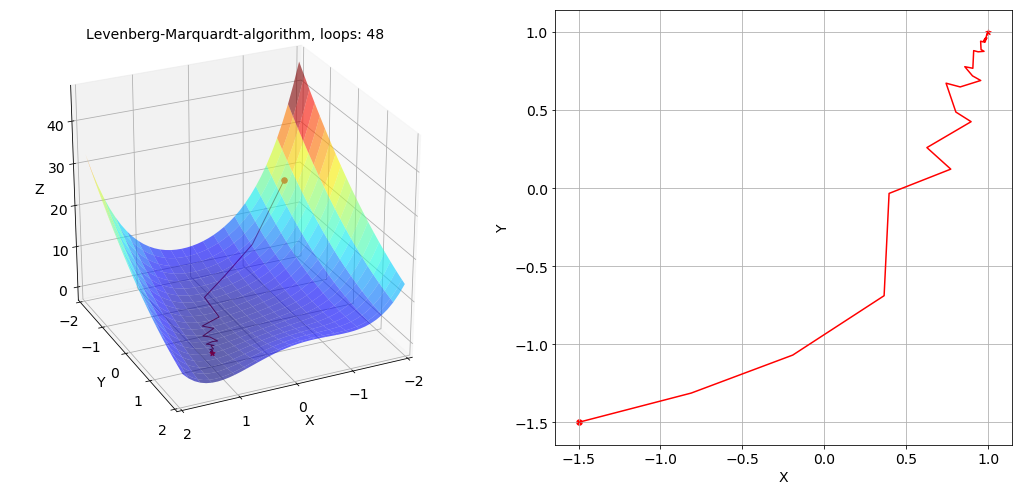
然后给出未知最优参数情况下LM算法的寻优路径及其在 x-y 平面投影的俯视图如下所示($\mu$ 的值固定为
无论是哪种情况,在两张图中都可以明显的看出LM算法较梯度下降算法收敛更加迅速,但是在最优值附近可能会发生震荡的现象。关于通过LM算法求 Rosenbrock 函数极小值的完整代码及 jupyter notebook 文件已上传至该 repo 的 codes 和 notebooks 文件夹:
脚注 (Footnote)
[1]:荀子·劝学 -- 荀况
[2]:Rumelhart D E, Hinton G E, Williams R J. Learning representations by back-propagating errors[J]. Cognitive modeling, 1988, 5(3): 1.
[3]:Vogl T P, Mangis J K, Rigler A K, et al. Accelerating the convergence of the back-propagation method[J]. Biological cybernetics, 1988, 59(4-5): 257-263.
[4]:Levenberg K. A method for the solution of certain non-linear problems in least squares[J]. Quarterly of applied mathematics, 1944, 2(2): 164-168.
[5]:Ван Л. Петросян О.Г. Распознавание лиц на основе классификации вейвлет признаков путём вейвлет-нейронных сетей // Информатизация образования и науки. 2018. №4. С. 129-139.