Golevka2001/Stereographic-Projection-of-Otto

通过球极投影的方式得到 otto 的多种形态

♿♿♿ Stereographic Projection of Otto ♿♿♿

                                    :-=++*++=-.
                                  +@@@@@@@@@@@@%+:
                                =%**##@@@@@@@@@@@@%=
                             .=#+. :::-+*%@@@@@@@@@@#.
                           .+#-   .-#+=--=++++**#%@@@@=
                         .*#-    .::-+*===+**##%###%@@@+
                        +%=:::....::----:-*##*+==+**#%@@=
                      =%+.::---:::::::. .=*##*++=+++*#%@@:
                    :%+:.::-=======-:.  :=*###*+=====+*#@#
                   +%-.::-=+++++===.   .-=*####*+=--==+*#@:
                  *%::::-=++++=====-:....-+*####**+===++*@*
                 *%:::::-=++*+=---===-:::-+**###****+++++#@
                +#:::::-==+#%%%*=--======++*******#**++++*@-
               +%:.:::--==*@@%%%##*+===++++***#####**+==++@=
              *%:.:::--===*@@#++*%%%#*+++**###%%%%%*++==++%*
             +%...::--====*%@@=...-****#%%%@@@@@@@@*++==+*#%
            =@:...:--=====+#%@@+. .. :-::=--+=+%@@%*++==+**@:
           .@-...:--======+**%@@#=:  .      :=#@@@%*++==**#@+
           %=....:-======++**##%@@@#*+-::---*%@@@@%**++=**#@#
          *#....:-=======+*****#%@@@@@@@@@@@@@@@@@%***+=*##%@.
         +%.....:-=======+******%%@@@@@@@@@@%@@@@@%#**+=*##%@=
        -@.....:-------==+******##%%***###%%@@@@@@##**+=*#%%@*
       .@-.....::-----===++******#%%%%%%%%@@@@@@@%###*++*#%%@*
      .%+......:::---====++*******##%%%%%%%@@@@@@%###**+*#%%@*
      #*.......::---===+++++***********##%%@@@@%%####***##%%@-
     +%.......::----==+++++++******++***#%%%@%%######***#%%@%
    :@-......::----===++++++++++******##%%%%%########***#%%@:
    ##--------=====+++++++++**********##################%%@=

✋😆欧内的手，好汉，今天来点儿大家想看的东西。

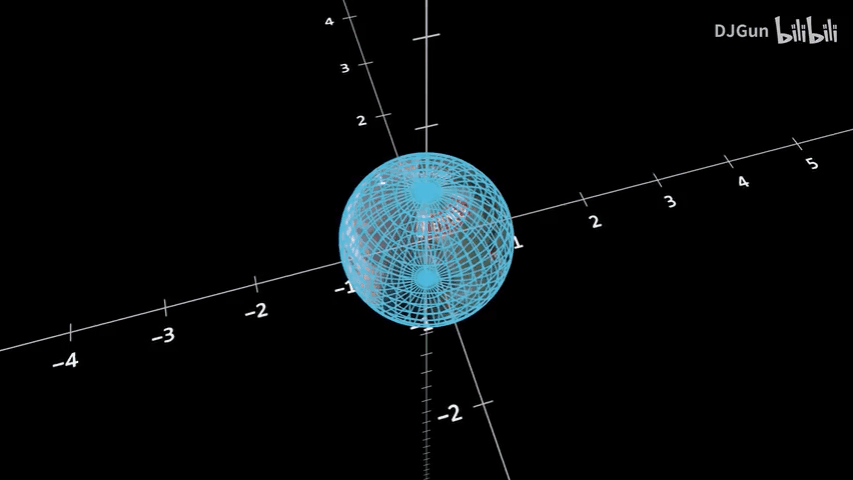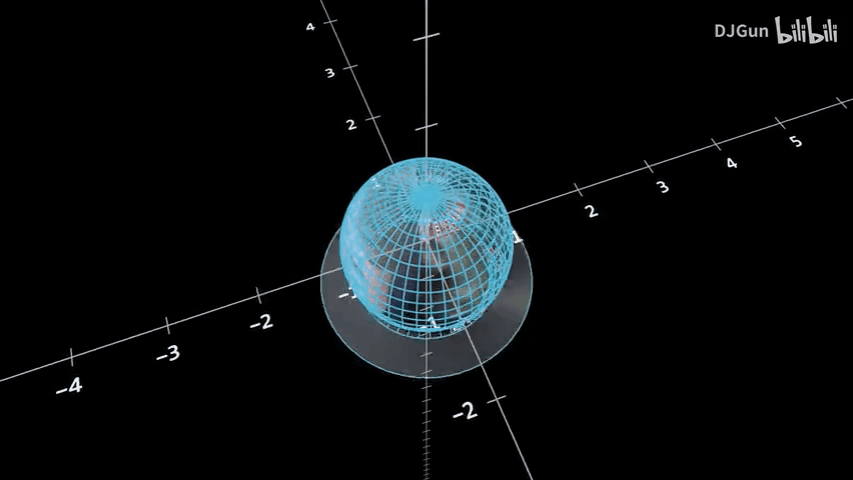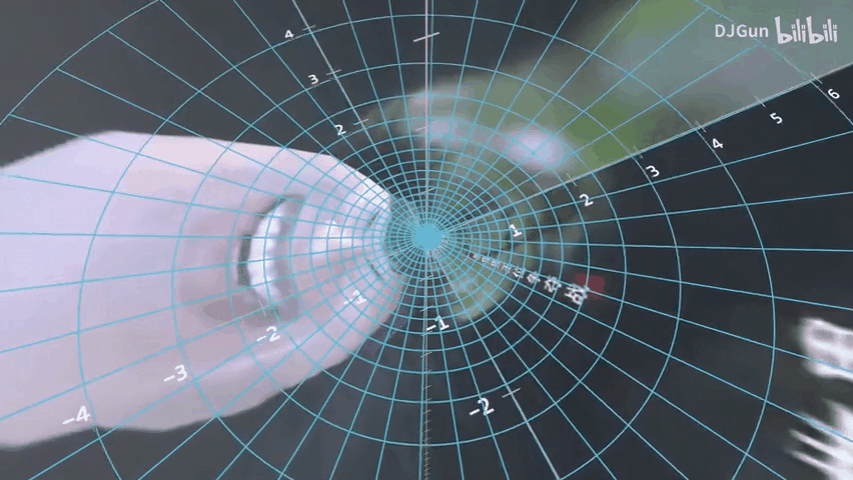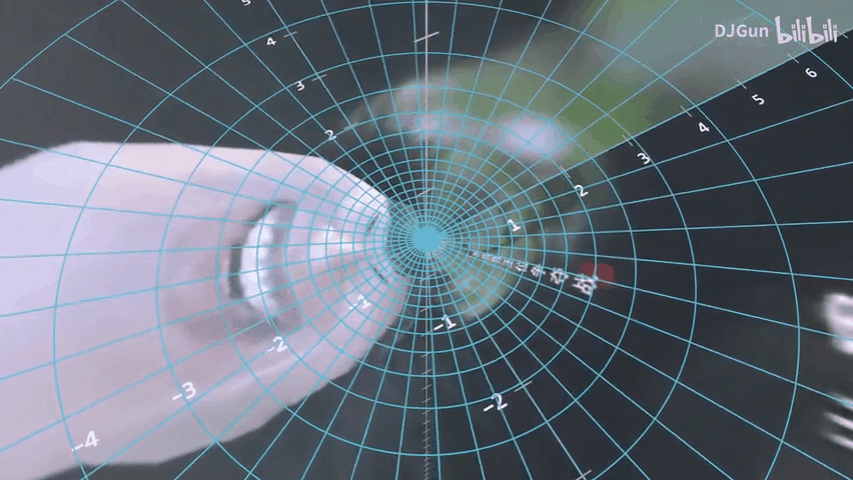
这是一个用于得到球面上的 $otto$ 在平面上的球极投影的程序。

通过改变球的角度，可以得到不同的投影，从而验证 $otto$ 的 “说的道理-栗子头二相性” 。

目录

• ♿♿♿ Stereographic Projection of Otto ♿♿♿
  • 目录
  • 前言
  • “说的道理”与“栗子头”的诞生
    • 选取原始图像
    • 将图片贴在球面上
    • 通过球极投影得到平面图像
    • 变换球的角度得到不同的投影
  • 数学推导
    • 计算投影平面上的点在球上的对应点坐标
    • 计算坐标系旋转后的坐标
    • 计算对应原始图像的点的坐标
  • 程序实现
  • 测试用例
    • 😆说的道理
    • 🌰栗子头
  • 使用说明
    • 下载 & 解压
    • 配置 Python 环境
    • 安装依赖库
    • 运行
    • 参数说明
  • 使用许可

前言

“球极投影是动物园的一次伟大实践与创新，是从欧透到说的道理与栗子头的必由之路，是动物园发展历程中的重大转折点，完成了鬼叫时代到道理时代的深刻变革。”

“说的道理”与“栗子头”的诞生

在 DJGun 发布的视频 《DJGun教你制作栗子头和说的道理》 中，说的道理与栗子头的生成方法得到公开。

得到说的道理和栗子头的具体过程如下：

选取原始图像

原始图像来自 @海绵宝宝小风儿 视频片头的古神语部分。

将图片贴在球面上

采用一般的球面投影方法得到球面上的 $otto$：

$$ \left\{ \begin{array}{l} x = r \cos{u} \sin{v} \\ y = r \sin{u} \sin{v} \\ z = r \cos{v} \end{array} \right. $$

通过球极投影得到平面图像

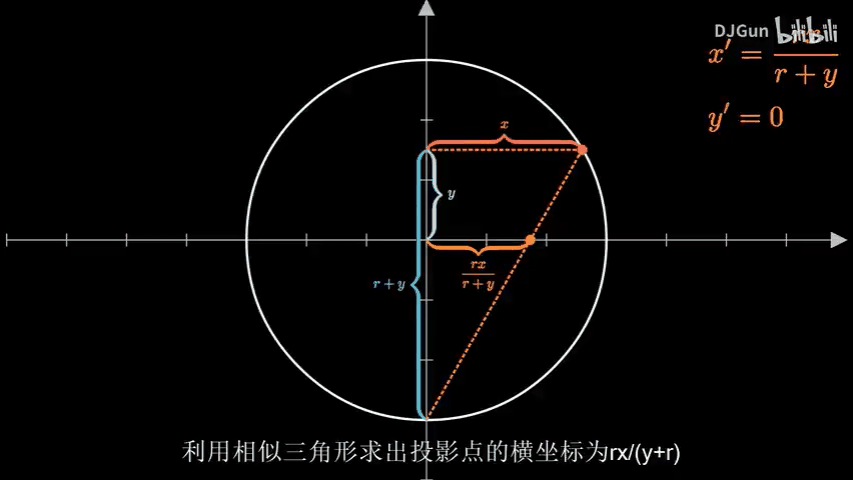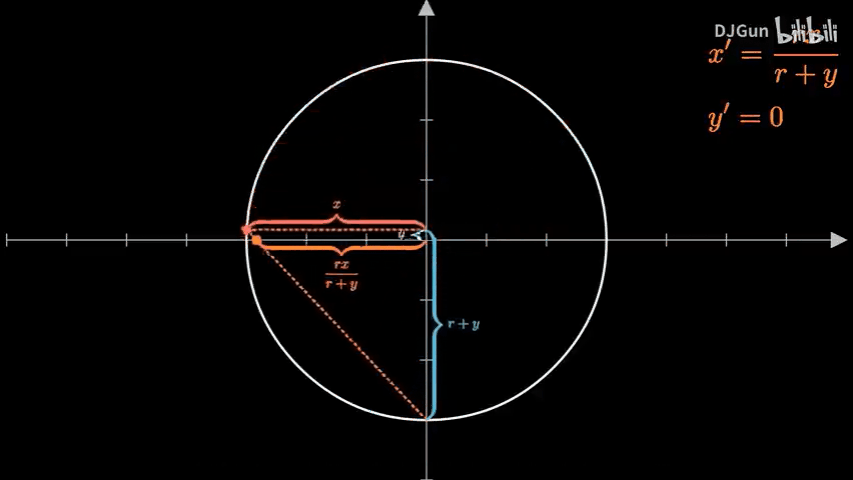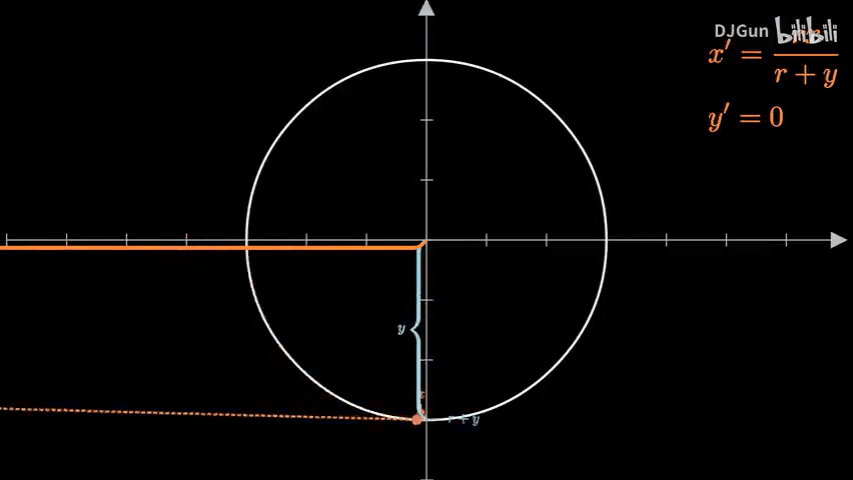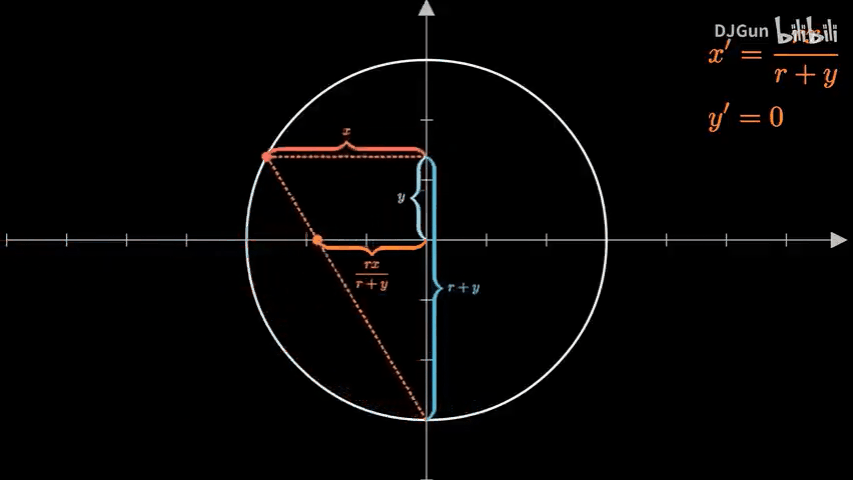
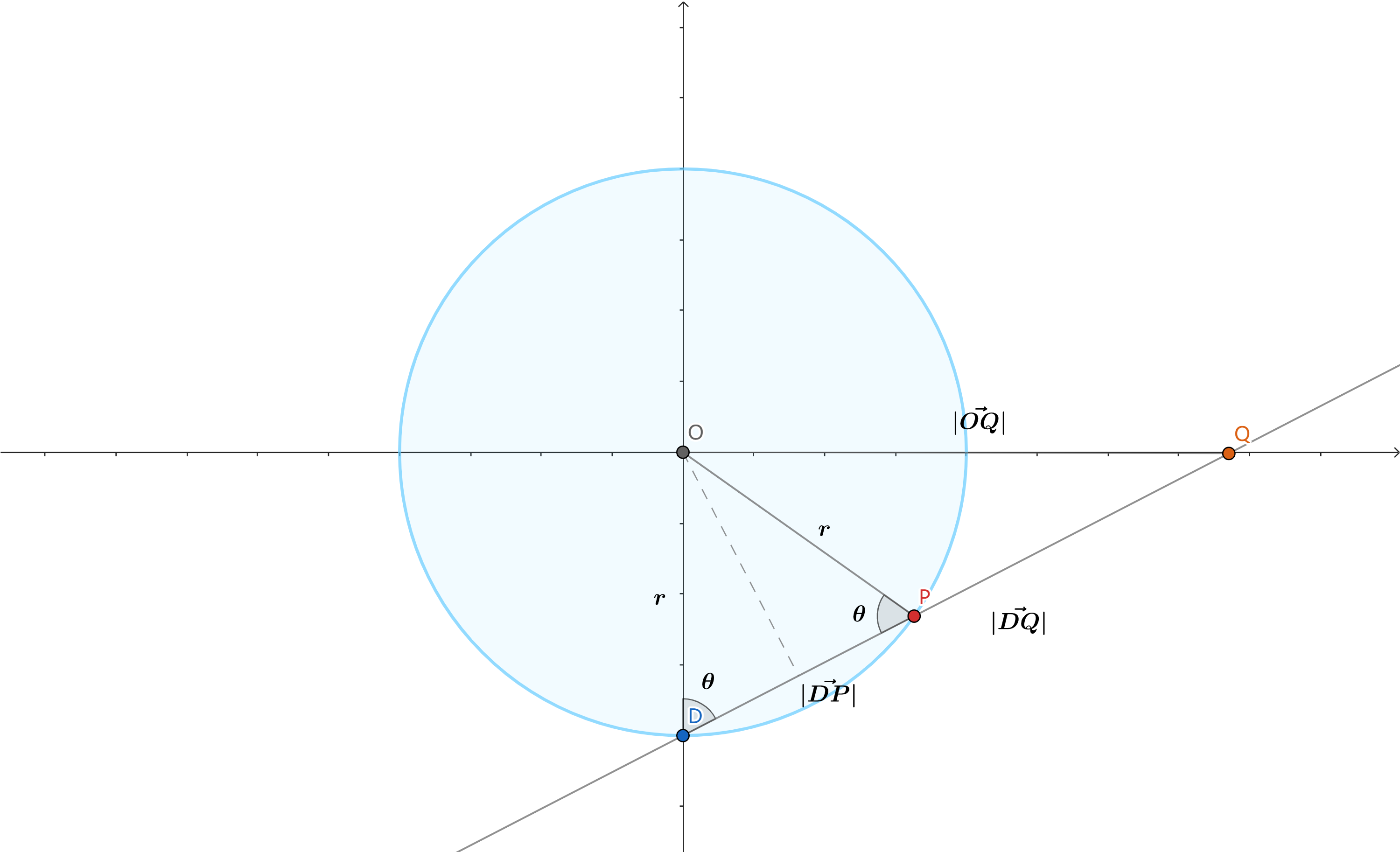
首先是在二维情况下分析得到的球极投影的方法：

将圆心置于坐标系原点 $O(0,0)$，以圆与 $y$ 轴负半轴的交点 $D(0,-r)$ 为投影点，投影落在直线 $y=0$ 上。

取圆上一点 $P(x,y)$，与投影点连接得到直线 $PD$，其与 $y=0$ 的交点为 $Q(x',0)$，则 $Q$ 为 $P$ 在直线 $y=0$ 上的球极投影。

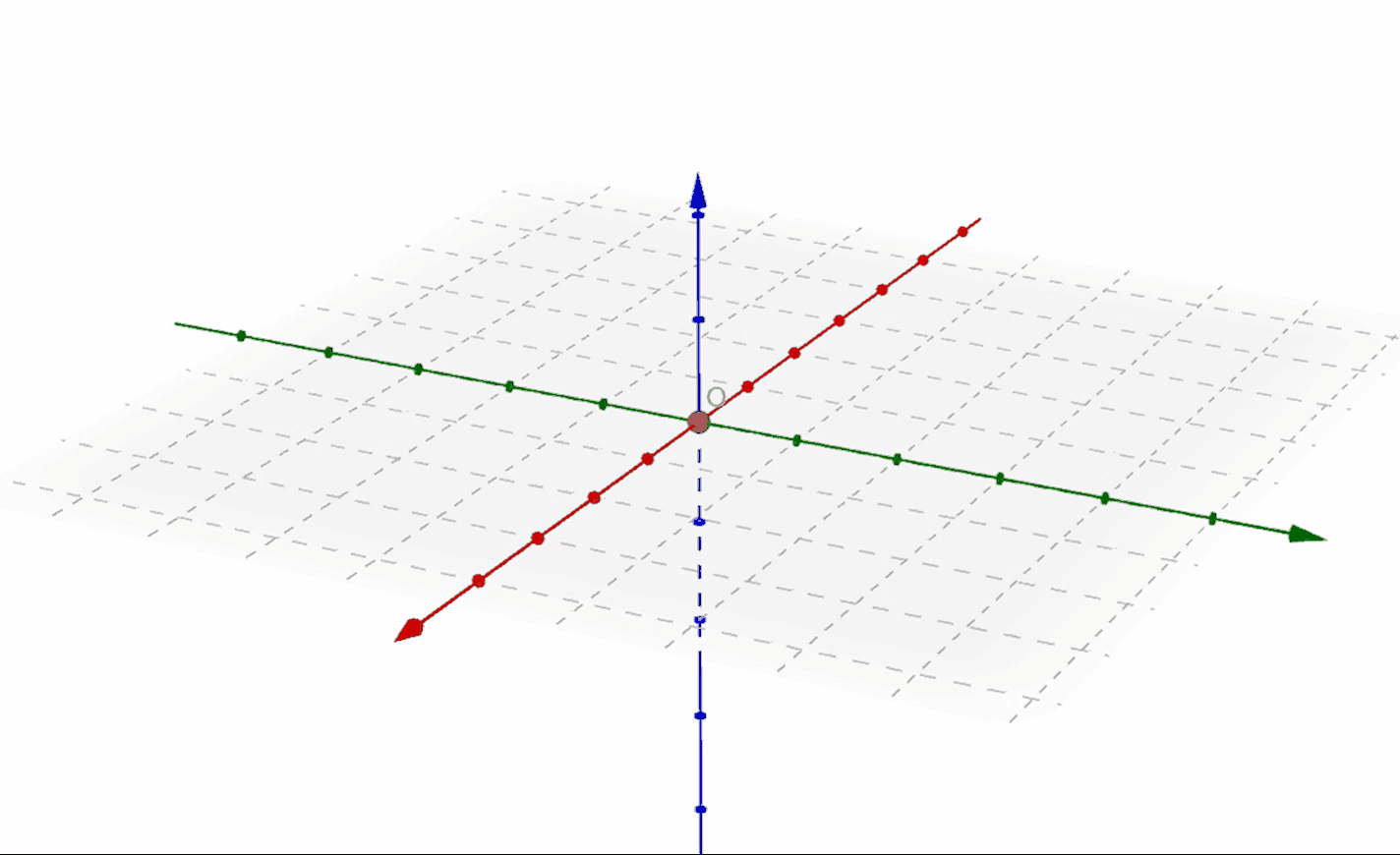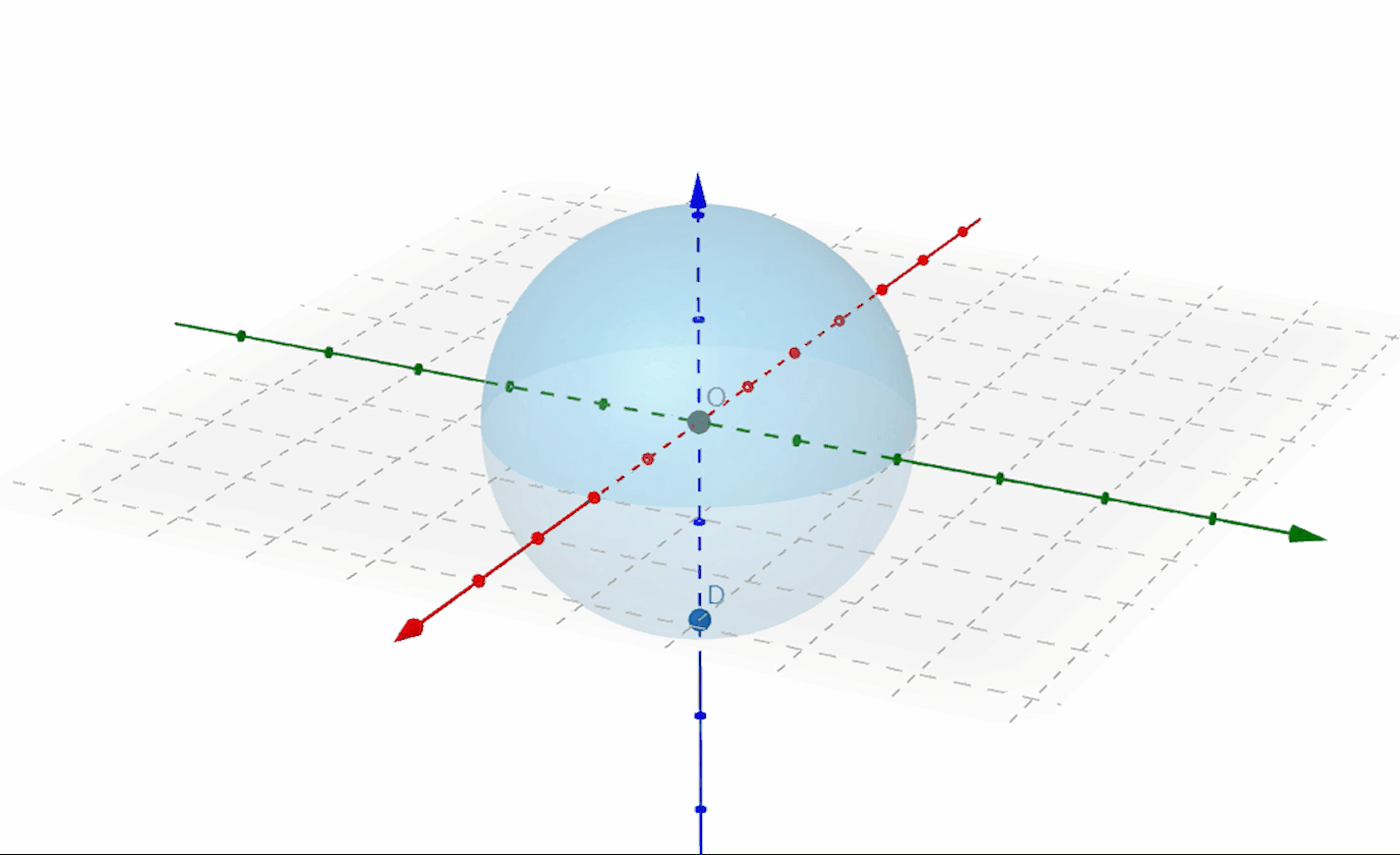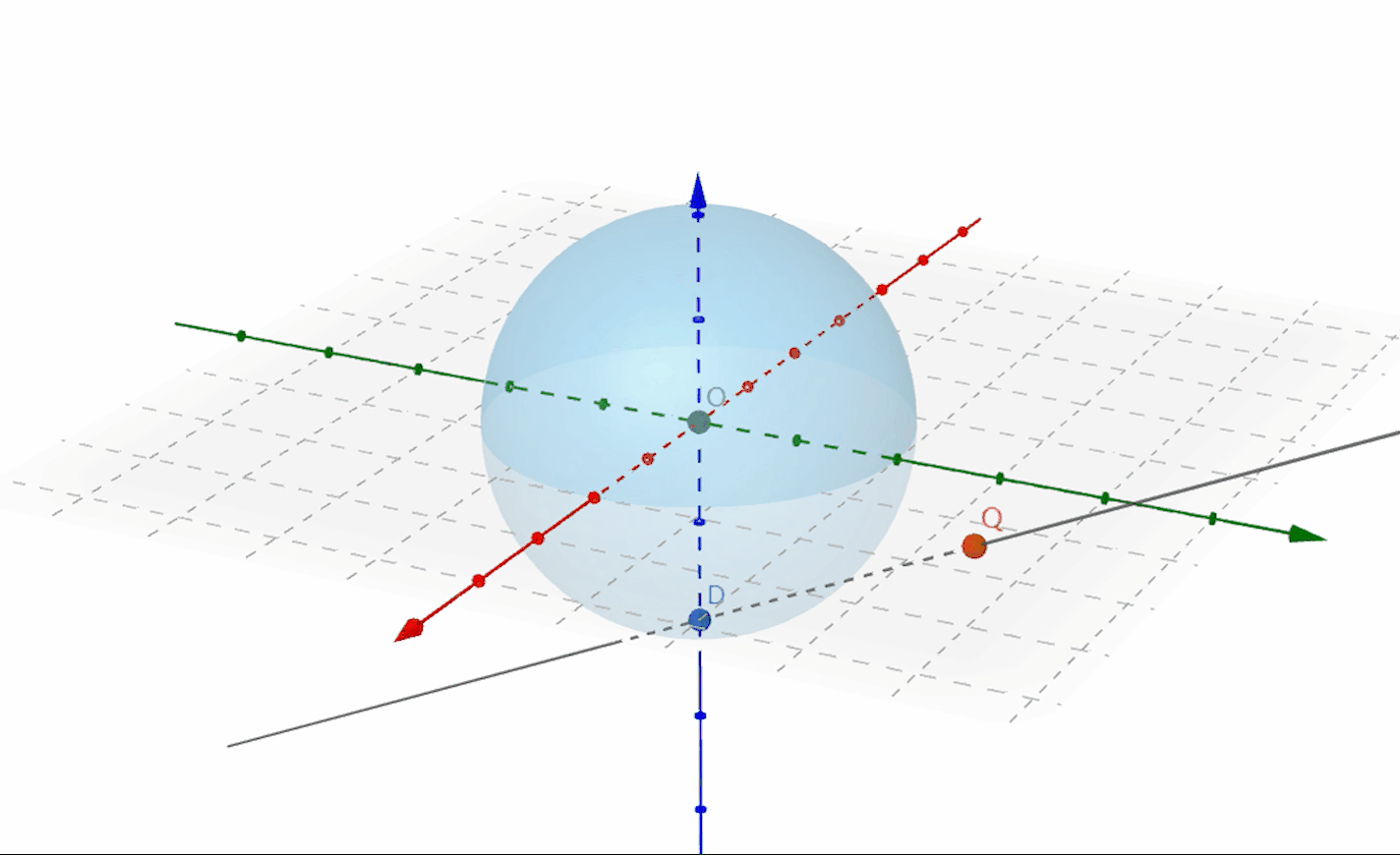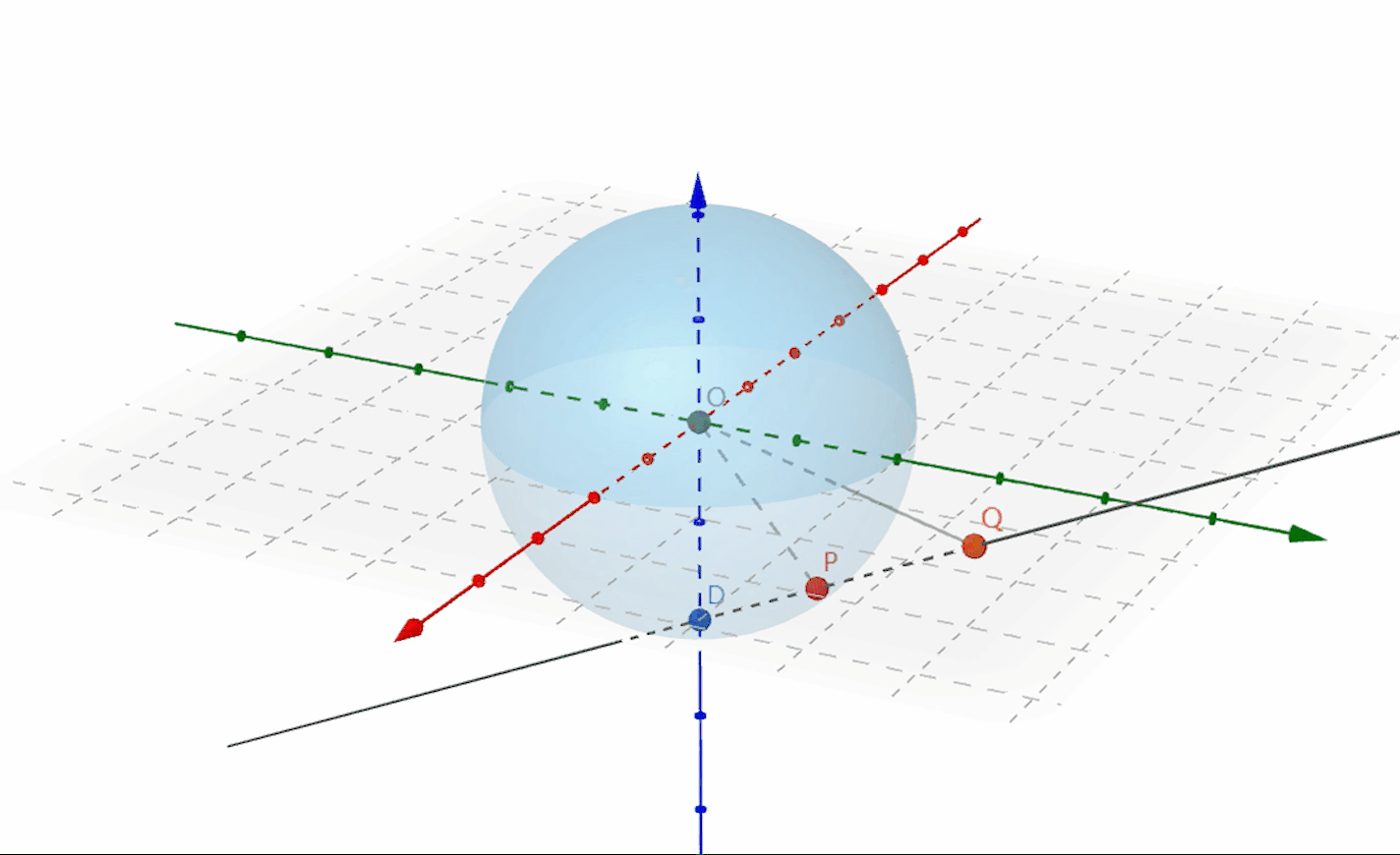
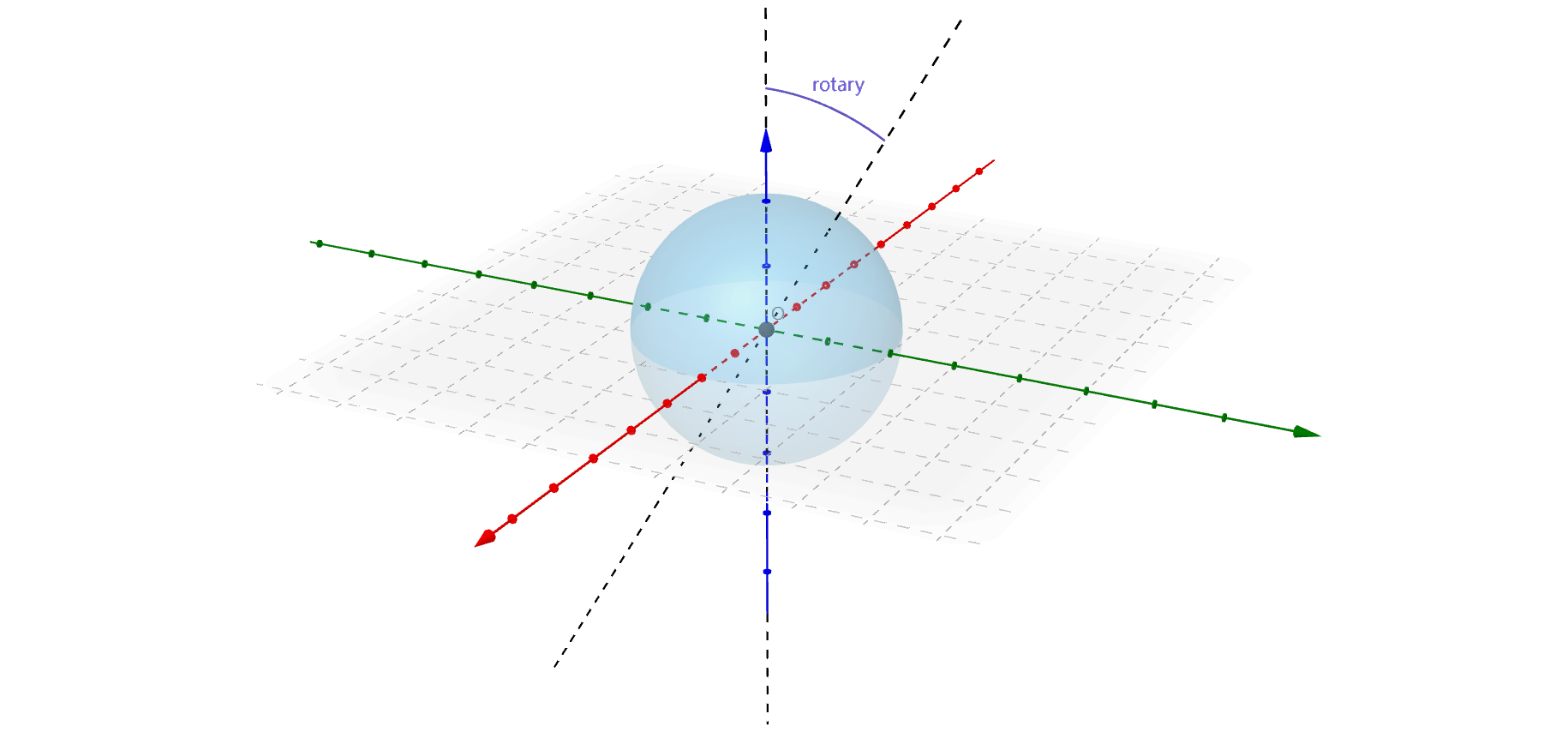
那么拓展到三维可以得到：

将球心置于坐标系原点 $O(0,0,0)$，以球与 $z$ 轴负半轴的交点 $D(0,0,-r)$ 为投影点，投影落在平面 $z=0$ 上。

取球上一点 $P(x,y,z)$，与投影点连接得到直线 $PD$，其与 $z=0$ 的交点为 $Q(x',y',0)$，则 $Q$ 为 $P$ 在平面 $z=0$ 上的投影。

按照这一方法，得到球面上的 $otto$ 在平面 $z=0$ 上的球极投影：

变换球的角度得到不同的投影

在上一步骤中，我们已经得到了说的道理，接下来通过变换球的角度得到栗子头。

至此，已经得到了说的道理和栗子头，并验证了 $otto$ 的 “说的道理-栗子头二相性” 。

下面进行程序上的实现。

数学推导

在进行程序实现前，需要先经过数学推导，得到目标图像上点到原图像上点的映射关系。

在上面D老师的演示中，是正向去得到的，而在程序实现中，需要从目标投影图像上的点开始，去反向推算出在原图像上的点的位置。

计算投影平面上的点在球上的对应点坐标

如前文所述，将球心置于坐标系原点 $O(0,0,0)$，以球与 $z$ 轴负半轴的交点 $D(0,0,-r)$ 为投影点，投影落在平面 $z=0$ 上。

根据所设定的目标图像的尺寸，遍历每个像素点。设其中一点为 $Q(x',y',0)$，与投影点 $D(0,0,-r)$ 连接得到直线 $QD$，其与球的交点为 $P(x,y,z)$，则 $P$ 为 $Q$ 在球上的对应点。

接下来计算点的坐标，为方便观察，在 $ODQ$ 所在平面上进行分析，以上几个点在平面上的关系如下图：

所需要求的是 $P$ 点的坐标，数学推导如下：

$求P点坐标，即向量 \vec{OP}：$

$\vec{OP} = \vec{OD} + \vec{DP}$

$已知有 \vec{OD} = (0,0,-r)，\vec{OQ} = (x',y',0)，|\vec{OD}| = |\vec{OP}| = r$

$下面须求 \vec{DP}：$

$\vec{DP} = |\vec{DP}| * \frac{\vec{DQ}}{|\vec{DQ}|}$

$\vec{DQ} = \vec{OQ} - \vec{OD} = (x',y',0) - (0,0,-r) = (x',y',r)$

$则 |\vec{DQ}| = \sqrt{x'^2 + y'^2 + r^2}$

$在等腰 \triangle ODP 中，|\vec{DP}| = 2 r \cos{\theta}$

$在 \triangle ODQ中，\cos{\theta} = \frac{|\vec{OD}|}{|\vec{DQ}|} = \frac{r}{\sqrt{x'^2 + y'^2 + r^2}}$

$|\vec{DP}| = 2 r \frac{r}{\sqrt{x'^2 + y'^2 + r^2}} = \frac{2r^2}{\sqrt{x'^2 + y'^2 + r^2}}$

$得到 \vec{DP} = \frac{2r^2}{\sqrt{x'^2 + y'^2 + r^2}}* \frac{(x',y',r)}{\sqrt{x'^2 + y'^2 + r^2}} = \frac{2r^2}{x'^2 + y'^2 + r^2} (x',y',r)$

$令 k = \frac{2r^2}{x'^2 + y'^2 + r^2}$

$综上，P = \vec{OP} = (0,0,-r) + k (x',y',r) = (kx',ky',(k-1)r)$

至此，得到了目标投影图像上的点 $Q$ 在球上的对应点 $P$ 的坐标。

计算坐标系旋转后的坐标

这里为便于计算把前面所述球的旋转转换为坐标系的旋转，设某点 $P(x,y,z)$ 变换后的坐标为 $P'(x',y',z')$，有以下结论：

绕 $x$ 轴旋转 $\alpha$ 角度：

$$ \left\{ \begin{array}{l} x' = x \\ y' = y \cos{\alpha} - z \sin{\alpha} \\ z' = y \sin{\alpha} + z \cos{\alpha} \end{array} \right. $$

可用矩阵表示为：

$$ \left[ \begin{array}{l} x' \\ y' \\ z' \end{array} \right] = \left[ \begin{array}{ccc} 1 & 0 & 0 \\ 0 & \cos{\alpha} & -\sin{\alpha} \\ 0 & \sin{\alpha} & \cos{\alpha} \end{array} \right] \left[ \begin{array}{l} x \\ y \\ z \end{array} \right] $$

绕 $y$ 轴旋转 $\beta$ 角度：

$$ \left\{ \begin{array}{l} x' = x \cos{\beta} + z \sin{\beta} \\ y' = y \\ z' = -x \sin{\beta} + z \cos{\beta} \end{array} \right. $$

可用矩阵表示为：

$$ \left[ \begin{array}{l} x' \\ y' \\ z' \end{array} \right] = \left[ \begin{array}{ccc} \cos{\beta} & 0 & \sin{\beta} \\ 0 & 1 & 0 \\ -\sin{\beta} & 0 & \cos{\beta} \end{array} \right] \left[ \begin{array}{l} x \\ y \\ z \end{array} \right] $$

绕 $z$ 轴旋转 $\gamma$ 角度：

$$ \left\{ \begin{array}{l} x' = x \cos{\gamma} - y \sin{\gamma} \\ y' = x \sin{\gamma} + y \cos{\gamma} \\ z' = z \end{array} \right. $$

可用矩阵表示为：

$$ \left[ \begin{array}{l} x' \\ y' \\ z' \end{array} \right] = \left[ \begin{array}{ccc} \cos{\gamma} & -\sin{\gamma} & 0 \\ \sin{\gamma} & \cos{\gamma} & 0 \\ 0 & 0 & 1 \end{array} \right] \left[ \begin{array}{l} x \\ y \\ z \end{array} \right] $$

那么，根据矩阵乘法的结合律，可以得到，经过变换后的坐标为：

$$ \left[ \begin{array}{l} x' \\ y' \\ z' \end{array} \right] = \left[ \begin{array}{ccc} \cos{\gamma}\cos{\beta} & \cos{\gamma}\sin{\beta}\sin{\alpha} - \sin{\gamma}\cos{\alpha} & \cos{\gamma}\sin{\beta}\cos{\alpha} + \sin{\gamma}\sin{\alpha} \\ \sin{\gamma}\cos{\beta} & \sin{\gamma}\sin{\beta}\sin{\alpha} + \cos{\gamma}\cos{\alpha} & \sin{\gamma}\sin{\beta}\cos{\alpha} - \cos{\gamma}\sin{\alpha} \\ -\sin{\beta} & \cos{\beta}\sin{\alpha} & \cos{\beta}\cos{\alpha} \end{array} \right] \left[ \begin{array}{l} x \\ y \\ z \end{array} \right] $$

计算对应原始图像的点的坐标

根据球面投影的坐标变换公式：

$$ \left\{ \begin{array}{l} x = r \cos{u} \sin{v} \\ y = r \sin{u} \sin{v} \\ z = r \cos{v} \end{array} \right. $$

写出逆变换公式：

$$ \left\{ \begin{array}{l} u = \arctan{\frac{y}{x}} \\ v = \arccos{\frac{z}{r}} \end{array} \right. $$

这里 $u$ 和 $v$ 的值域分别为 $[0, 2\pi)$ 和 $[0, \pi]$，需要再根据原始图像的尺寸大小，将 $u$ 和 $v$ 的值域映射到 $[0, w)$ 和 $[0, h)$：

$$ \left\{ \begin{array}{l} u' = \frac{u}{2\pi} w \\ v' = \frac{v}{\pi} h \end{array} \right. $$

转为整形并做边界检查。

至此，已经完成了从投影图像像素点到原始图像像素点的映射的推导。

程序实现

main.py

测试用例

😆说的道理

参数：

• 原始图像：otto.png
• 图像尺寸：400 * 300
• 垂直方向偏移量：0.4
• 缩放倍数：1.5
• 旋转角度： $\alpha = \gamma = 0 \degree$， $\beta = -5 \degree$

🌰栗子头

参数：

• 原始图像：otto.png
• 图像尺寸：400 * 300
• 垂直方向偏移量：-0.4
• 缩放倍数：1
• 旋转角度： $\alpha = \gamma = 0 \degree$， $\beta = 155 \degree$

使用说明

本项目使用 Python 编写，依赖 numpy 库进行主要的数学运算。

下载 & 解压

点击右上方的绿色 Code 按钮，在下拉菜单中点击 Download ZIP 下载完成后，把它解压到你想要的位置。

配置 Python 环境

略。

安装依赖库

pip install numpy

运行

编辑 main.py 文件，按需修改开头部分的相关参数。

参数调整完成后，编译运行，在所设定的输出路径下找到生成的投影图像。

参数说明

1. 路径（相对、绝对路径均可）

path_img：原始图像

path_proj：输出的投影图像

2. 输出的投影图像尺寸（像素）

w_proj：宽

h_proj：高

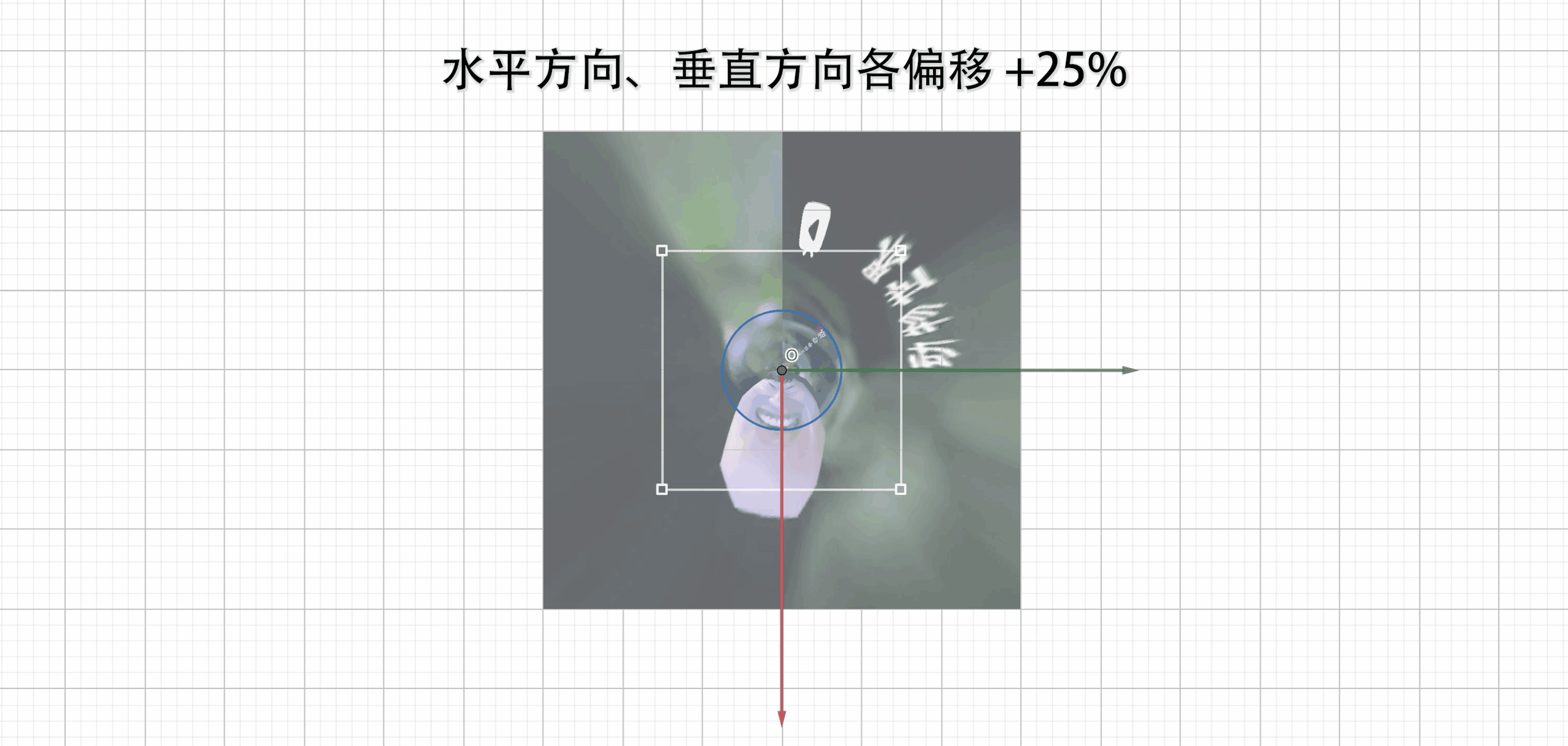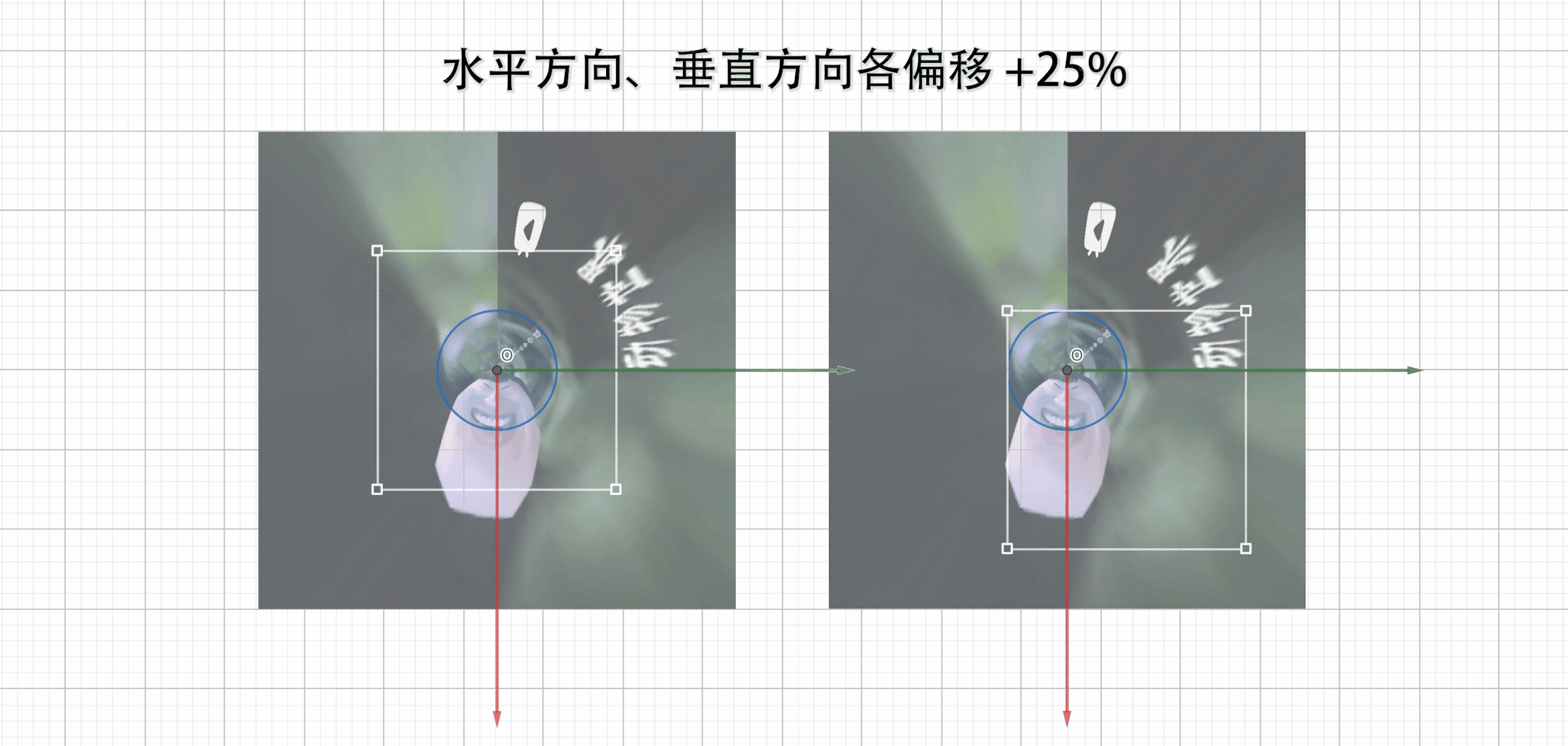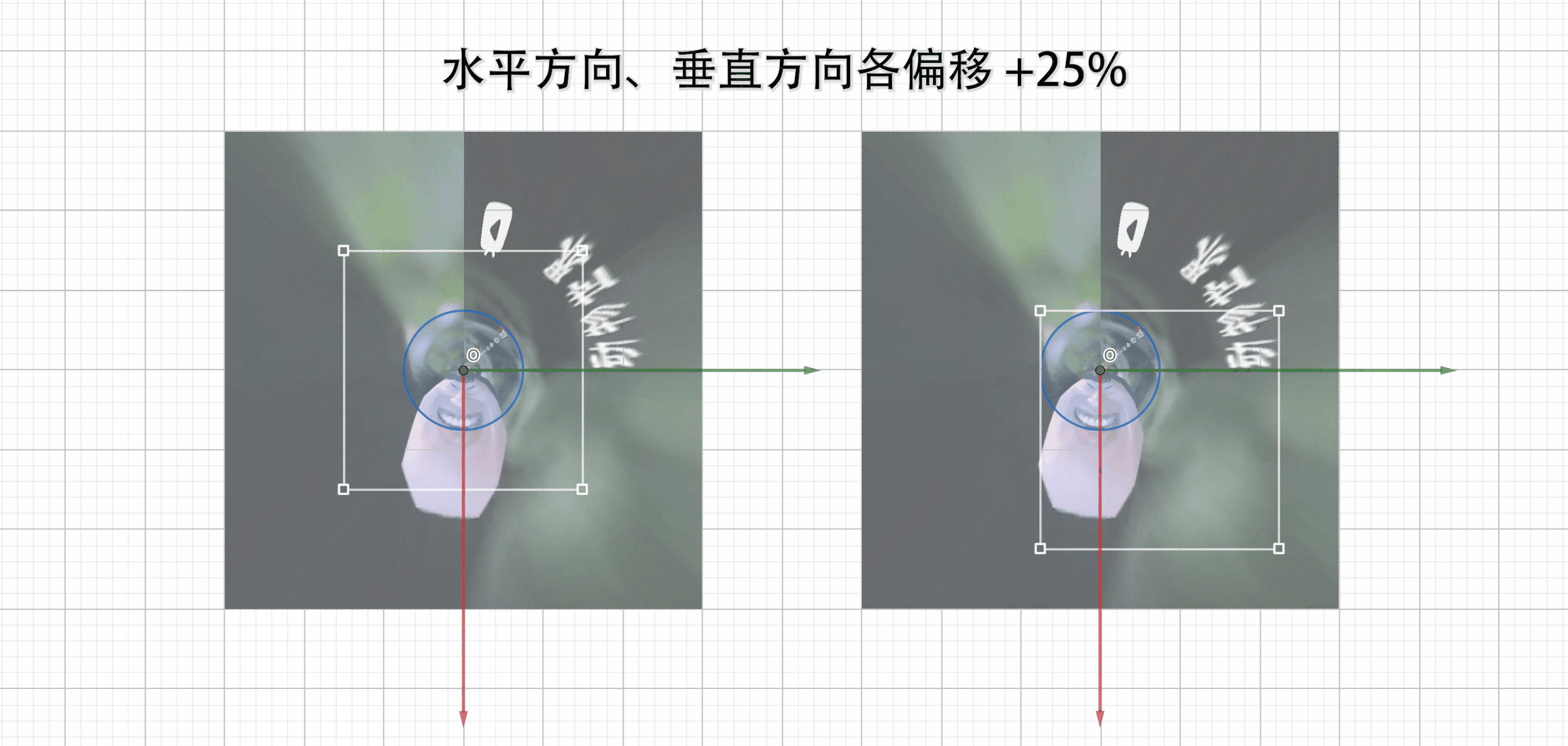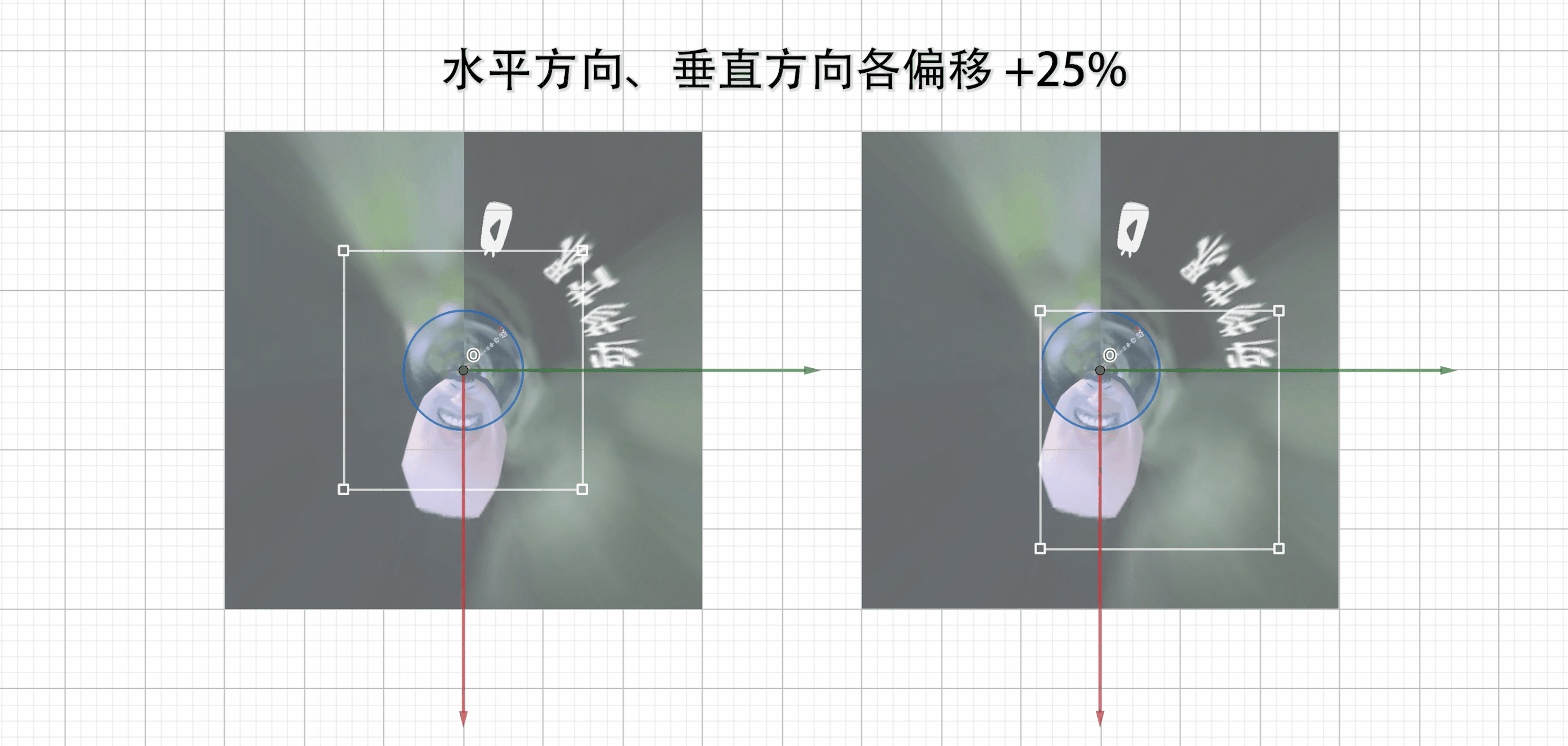
3. 偏移量（百分比）

offset_hor：水平方向（向右为正）

offset_ver：垂直方向（向下为正）

输出的投影图像相当于在整个投影平面下取了一个矩形区域，以上两个参数就是调整该矩形在投影平面的位置。

均为 0 时，输出的图像中心与坐标轴原点重合；例如当两个偏移量均为 $\frac{1}{4}$ 时，投影图像范围变换如下图白框所示：

4. 缩放倍数

scale：缩放倍数

这里的缩放倍数实际是调整球的半径，在前面的数学推导中可以看到，对于相同尺寸的投影区域，球的半径越大，输出图像中包含的内容越少，相当于放大了图像；相反地，球的半径越小，则相当于缩小了图像。

5. 旋转角度（度）

alpha：绕 $x$ 轴旋转

beta：绕 $y$ 轴旋转

gamma：绕 $z$ 轴旋转

是通过坐标系的旋转等效为球上贴图的旋转来实现的，从而得到 $otto$ 的不同形态。

坐标系的旋转除我在前文的推导外，也可以参考 “欧拉角-四元数的转换” ，不再赘述。

使用许可

MIT © Gol3vka.