Live demo: https://huggingface.co/spaces/GreenWizard2015/dog-breed-classification-app
A while ago, I worked on a project for a friend who wanted to develop a dog breed identification bot based on images. Instead of using an existing solution, I decided to take on the challenge and experiment with my own approach.
For the project, I started with a common setup using MobileNetV2 as the encoder, which is a popular convolutional neural network architecture used for image classification tasks. To perform the actual classification, I implemented a simple Multi-Layer Perceptron (MLP). However, instead of using the regular softmax activation function, I opted for the hyperspherical softmax.
The regular softmax function treats each class as an independent classifier. It learns to produce the strongest signal or score when presented with data corresponding to its respective class. While this approach is straightforward and works reasonably well, it has some limitations. One of the limitations is that it does not explicitly model the relationships between different classes.
On the other hand, the hyperspherical softmax operates on a hypersphere and takes advantage of the underlying geometry. It considers each class as a point on the hypersphere's surface. This approach allows for a better representation and modeling of the relationships between classes. By considering the geometry of the hypersphere, the hyperspherical softmax can capture complex relationships among classes and provide a more nuanced understanding of the data.
In terms of performance, the overall top-1 accuracy of the model did not change significantly and was mainly limited by the capabilities of the MobileNetV2 backbone architecture. However, the top-K accuracy, which measures how far the model's predictions are from the ground truth, proved to be quite interesting. While we would ideally want the model to always provide a single and correct answer, this is often naive and not always feasible.
The top-K accuracy is important because it allows us to understand the model's confidence and uncertainty in its predictions. By considering multiple possible answers within the top-K predictions, we gain insights into the model's level of certainty. This is particularly valuable in scenarios where the model needs to provide a ranked list of possible dog breeds based on the input image. Users can have a better understanding of the model's confidence and explore alternative options if the top-ranked prediction seems uncertain.
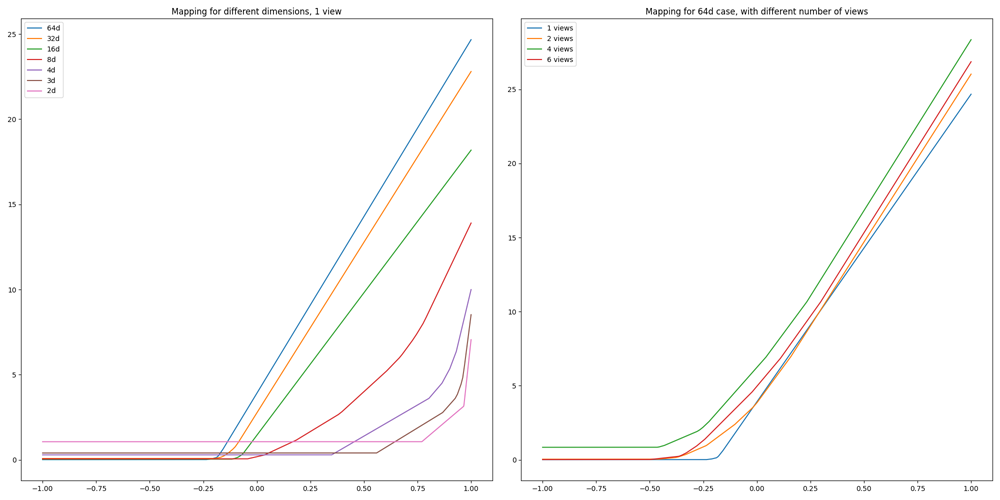
In the initial version of the project, I used a handcrafted method to convert cosine similarity into scores/probabilities. However, this approach proved to be ineffective, leading me to adopt a learnable mapping for this purpose.
The learnable score function is implemented using a tiny neural network (1-16-16-1). This network solely operates on the metric of similarity between the predicted point and the reference points of the classes. By using this network, I can map the similarity metric to a score that represents the model's confidence in its prediction.
One crucial aspect of this mapping is that the weights of the network are constrained to be positive. This constraint ensures that the mapping is strictly increasing, meaning that as the similarity metric increases, the corresponding score also increases. This is important because it allows for a clear ranking of predictions based on their scores.
To enhance the robustness and shape the prediction space, data augmentations are used during training. These augmentations are applied sequentially, so the first image is very similar to the original, and each subsequent image becomes progressively more challenging to recognize. By introducing variations to the input images, the model becomes more adept at capturing even subtle features for accurate dog breed identification.
Augmentations can include operations such as random rotations, translations, scaling, flips, and changes in brightness or contrast. These transformations simulate different real-world scenarios and help the model generalize better to unseen data. For example, if the original image shows a dog in a specific orientation, rotating the image by a few degrees can make the model more robust to dogs appearing at different angles.
During training, the model predicts the breed of each augmented image, and additional loss is computed between the predictions of different versions of the original image. This additional loss encourages the neural network to learn features that are invariant to the applied augmentations. In other words, the model learns to recognize important characteristics of a dog breed regardless of changes in rotation, scale, or other transformations.
This is particularly important when using hyperspherical softmax as it allows for refining the boundaries between classes. By applying data augmentations and incorporating additional loss, the model becomes more robust to variations and can better distinguish between different dog breeds.
The results of the ablation study indicate that a greater number of views enables the neural network to learn more gradual class boundaries. Additionally, increasing the dimensionality of the hypersphere allows the neural network to learn smoother class boundaries by creating more space between the classes. When the dimensionality is limited to 2, the neural network has a very restricted amount of space available, resulting in sharp boundaries. Based on my findings, it is clear that these factors significantly impact the smoothness of class separation.