Jimmy owns a garden in which he has planted N trees in a row. After a few years, the trees have grown up and now they have different heights.
Jimmy pays much attention to the aesthetics of his garden. He finds his trees aesthetically pleasing if they alternately increase and decrease in height (..., shorter, taller, shorter, taller, ...).
These are examples of aesthetically pleasing trees:
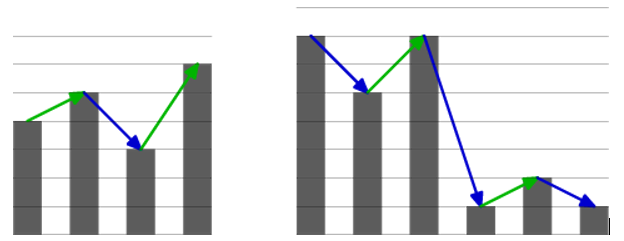
These are examples of trees that are not aesthetically pleasing:
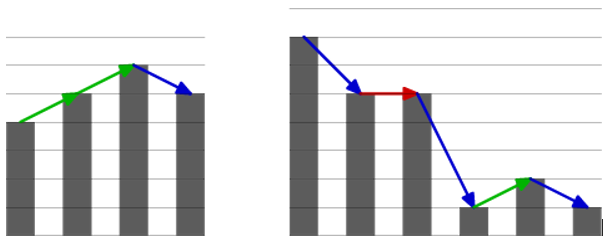
Note that two adjacent trees cannot have equal heights. It may turn out that some trees have to be cut out, in order to keep the remaining trees aesthetically pleasing. However, there is a legal restriction that allows a gardener to cut out at most one tree in his possession. In how many ways can Jimmy cut out exactly one tree, so that the remaining ones are aesthetically pleasing?
Write a function:
func Solution(A []int) int {}that, given an array A consisting of N integers, where A[K] denotes the height of the K-th tree, returns the number of ways of cutting out one tree, so that the remaining trees are aesthetically pleasing. If it is not possible to achieve the desired result, your function should return −1. If the trees are already aesthetically pleasing without any removal, your function should return 0.
Examples:
-
Given A = [3, 4, 5, 3, 7] your function should return 3:
● You can remove A[0] so the sequence becomes [4, 5, 3, 7];
● You can remove A[1] so the sequence becomes [3, 5, 3, 7];
● You can remove A[2] so the sequence becomes [3, 4, 3, 7].
-
Given A = [1, 2, 3, 4] your function should return −1, since there is no single tree that Jimmy can cut out that would leave the rest of the trees looking aesthetically pleasing.
-
Given A = [1, 3, 1, 2] your function should return 0, since the trees are already aesthetically pleasing and no removal is needed.
-
Assume that:
● N is an integer within the range [4..200];
● each element of array A is an integer within the range [1..1,000].
Check /calculations/tree.go for solution.
First check tree list to see if they are already aesthetically pleasing (0).
Then iterate through the tree list: remove a tree at each index and check the remaining trees for aesthetics. If there are no instances where the remaining trees are aesthetically pleasing, then the entire tree list will be -1. Otherwise, add up the number of instances where the remaining trees are aesthetically pleasing and return this value.
Since performance is not an issue, we can afford to do O(n^2) time.
Go to /calculations directory and run
go test
Test file: /calculations/tree_test.go
Test cases: -1 (one instance), -1 (two instances), 0, 2 (forward), 2 (backward), 3 (forward), 3 (backward)