A python geological mesh software to verticalize and horizontalize faults and horizons. This work is based on the least squares lecture of Dmitri Sokolov. The work done is described in the following repository. See main for more details.
There are four geological slices called chevron, ifp1, ifp2 and shell. These slices describe 2D geological models having zero or more faults and some horizons. Each mesh has different object files describing either the slice, the horizons or the set of faults. Slices can have different connex components. The attributes.py files contains preprocessed data about horizon's and fault's edges. Mesh class is coded in mesh.py.
We processed the mesh using the following scheme, for each dimension (x, y):
- Load the mesh
- Constructs containers for horizon's and fault's edges
- Beautify triangles while keeping the original shape
- Horizontalize geological stratifications / verticalize faults
- Write output mesh
Editing the mesh amounts to minimizing energy functions. Hence, we use least square's formulation for our problem. In our work, we mainly:
- Optimized the triangles using Poisson's equation
- Minimized distance between some vertice's positions (for faults and horizons)
- Lower / raise vertices (for visualization purposes)
First the mesh has to be smoothed in order to show regular triangles.
For this, Poisson's equation has been implemented.
We minimized the difference of distances between the current edge length and the processed one. It was done for the x, and y coordinates.

In order to make a geological horizon flat, the y-coordinate variation was minimized, between a reference point and the origin vertice of each edge. The process has been repeated for each horizon, leading to the following result:

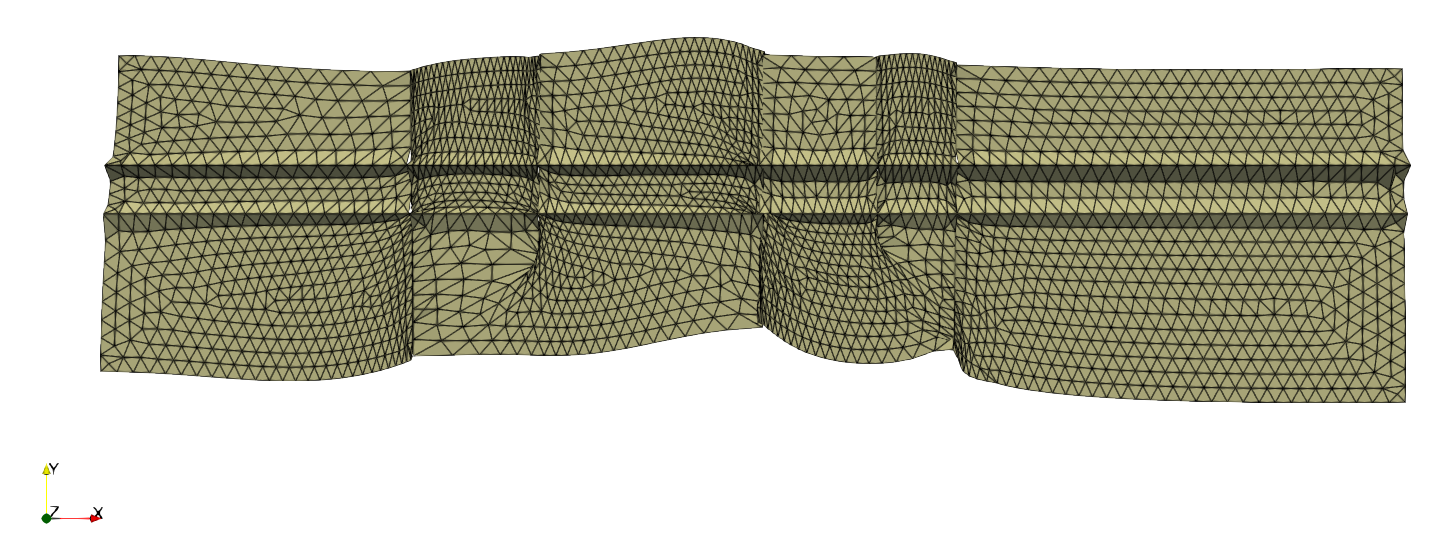
Concerning the fault, the aim is to minimize the x coordinate variation between the origin and destination vertices for each edge of the fault. With this condition the faults were verticalized.

Another condition must be added to prevent the connexe component from splitting. The connexe components were joined by minimizing the x distance between an edge and its opposite along the fault, the same was done for the y coordinate.
By applying together the minimizations mentioned above, the following results are obtained: