Reference:https://www.youtube.com/watch?v=xhO8iz2qCOE&t=627s
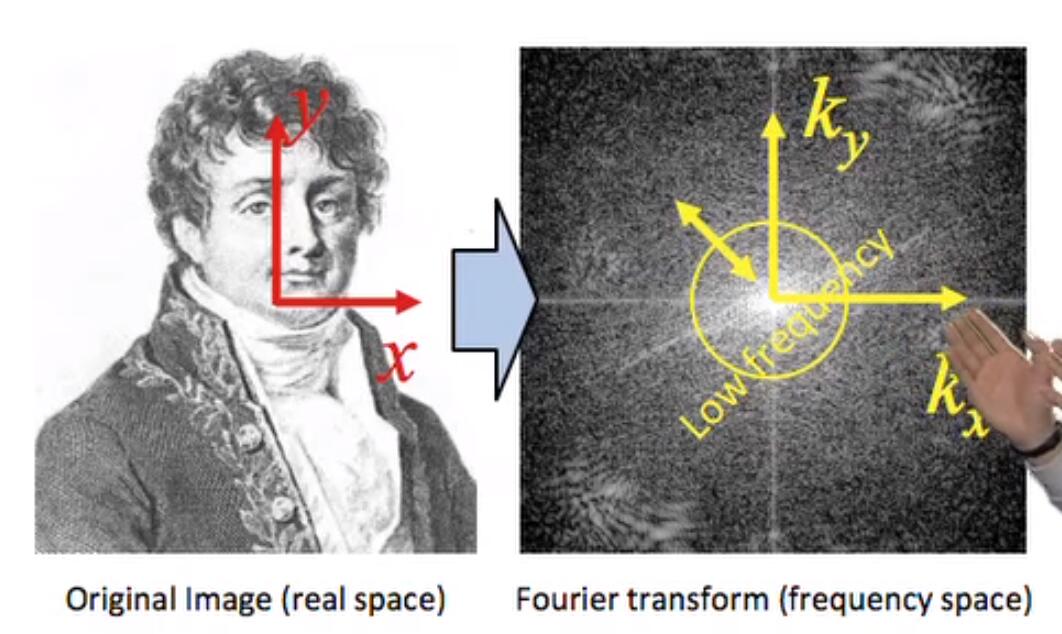
图像傅里叶变换是指对图像进行二维傅里叶变换,将图像上的点看作是时域上的周期信号,傅里叶变换后便成了频域上的信号。频域上利用不同多组不同频率的正弦(余弦)波来对原信号进行叠加,其最终频域上的图是利用k向量来表示一组信号,模长|k|代表频率w,其偏转角代表传播方向direction。
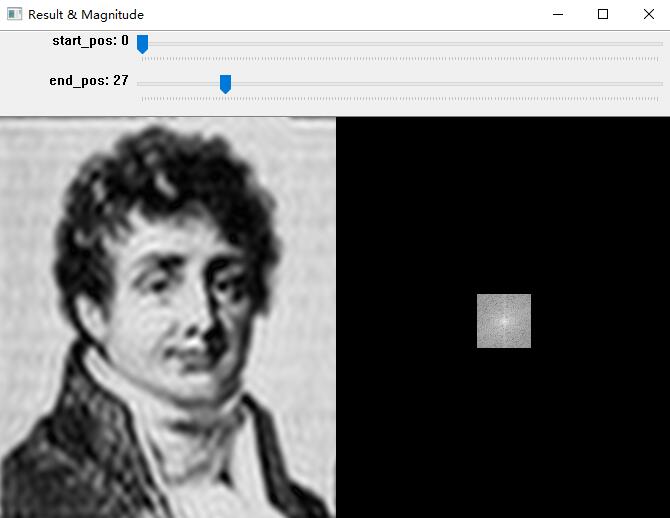
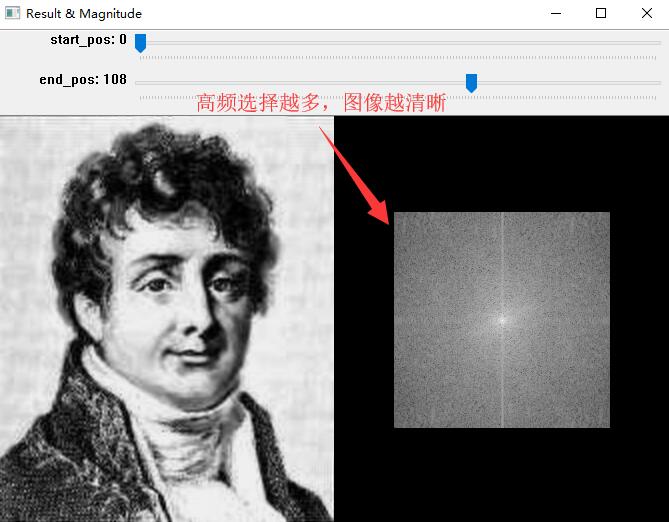
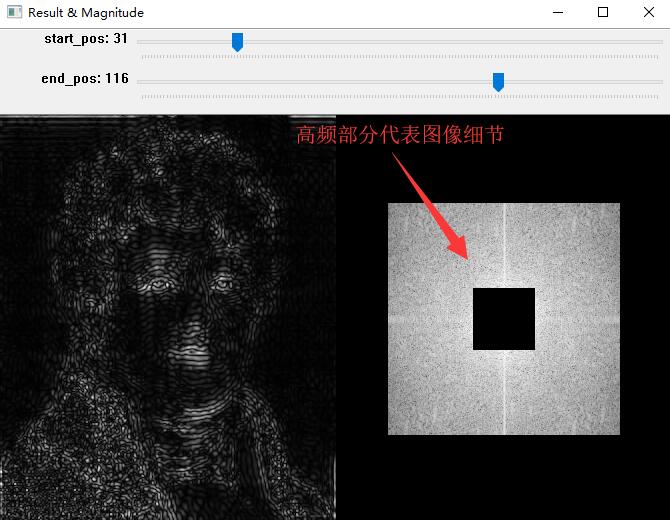
图片中的频率可理解为图像灰度值在平面上的变化梯度值,高频代表灰度值变化大(图像中的细节),低频代表灰度值变换平缓(图像中的平滑部分)。
- 对原图像进行傅里叶变换(得到复数矩阵)。(cv2.dft())
- 对频谱矩阵左上和右下调换,右上和左下调换,使得图片中心是整个频谱的最低频率点。(np.fft.ffshift())
- 将频谱图(梯度变换图)映射到可视化范围(0~255),使用np.log(cv2.magnitude())压缩数据范围。
- 因为cv2中如果图像数据是float型,opencv会自动乘以255再显示,因此需要将所有值压缩到0.0 ~ 1.0之间。
- 创建滤波器,滤掉部分高频(细节)或低频(轮廓)信号。
- 反shift,并逆fft变换。
- 同3一样,将结果进行数据归一化。