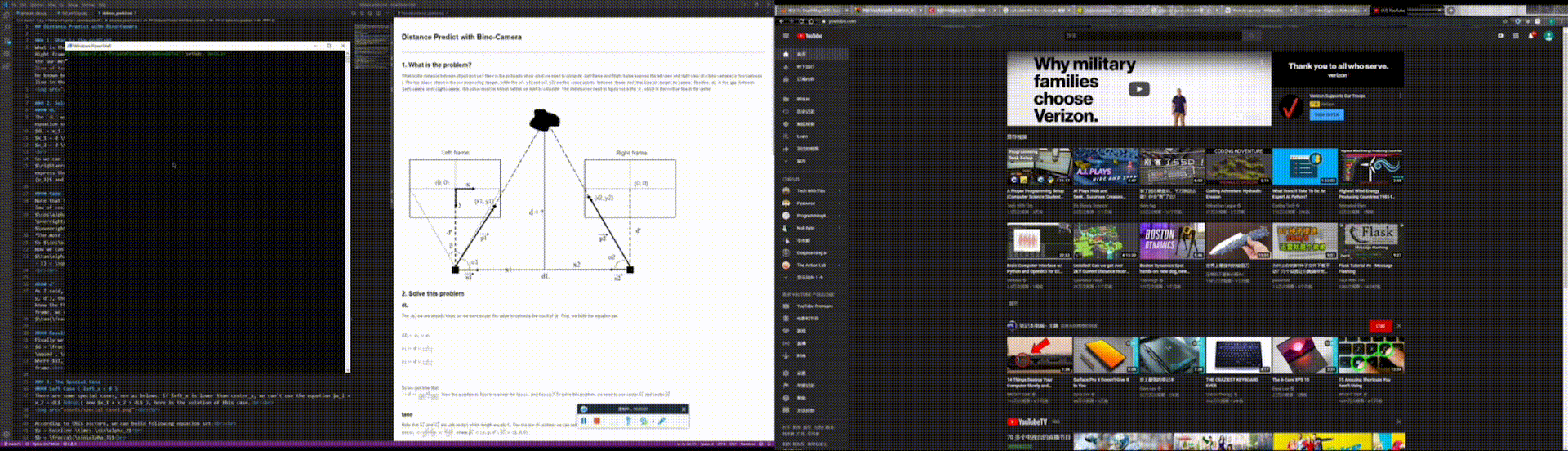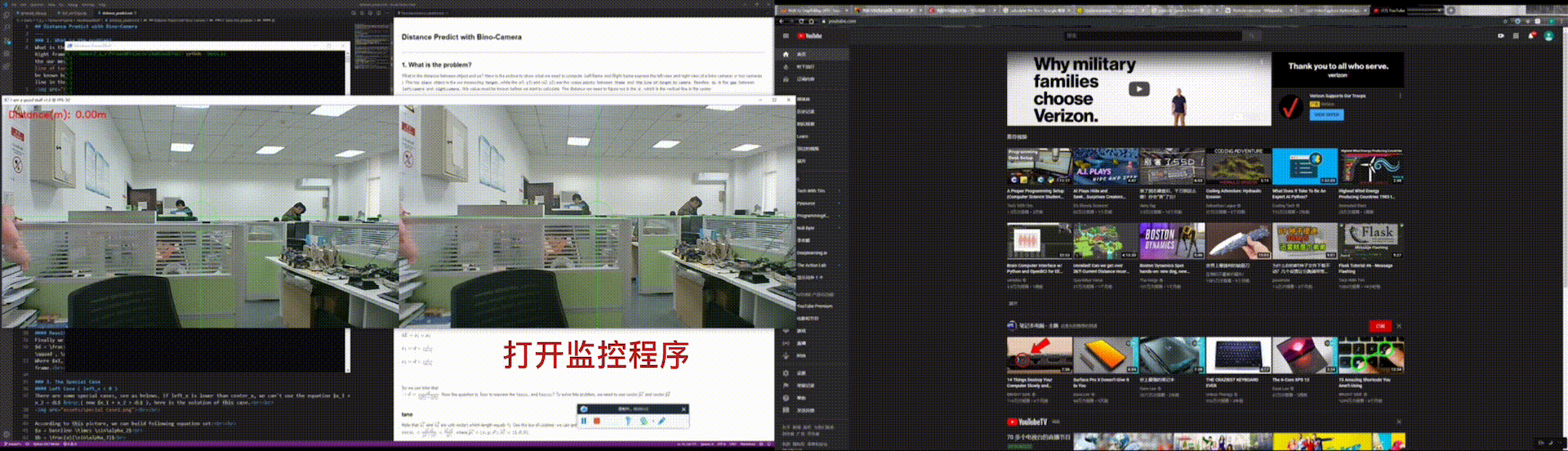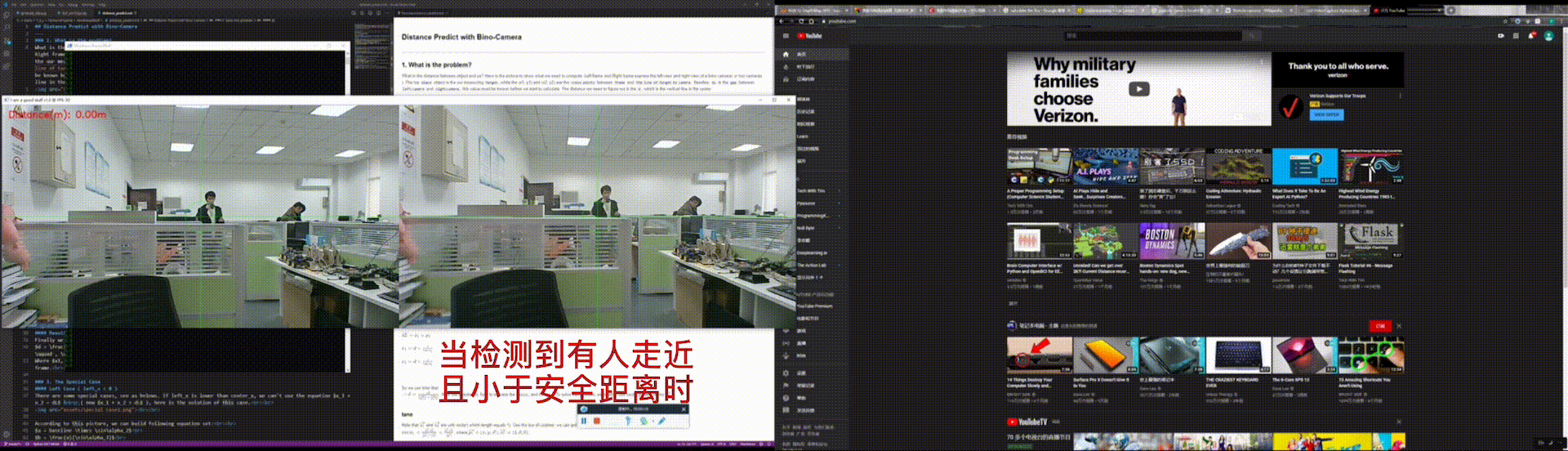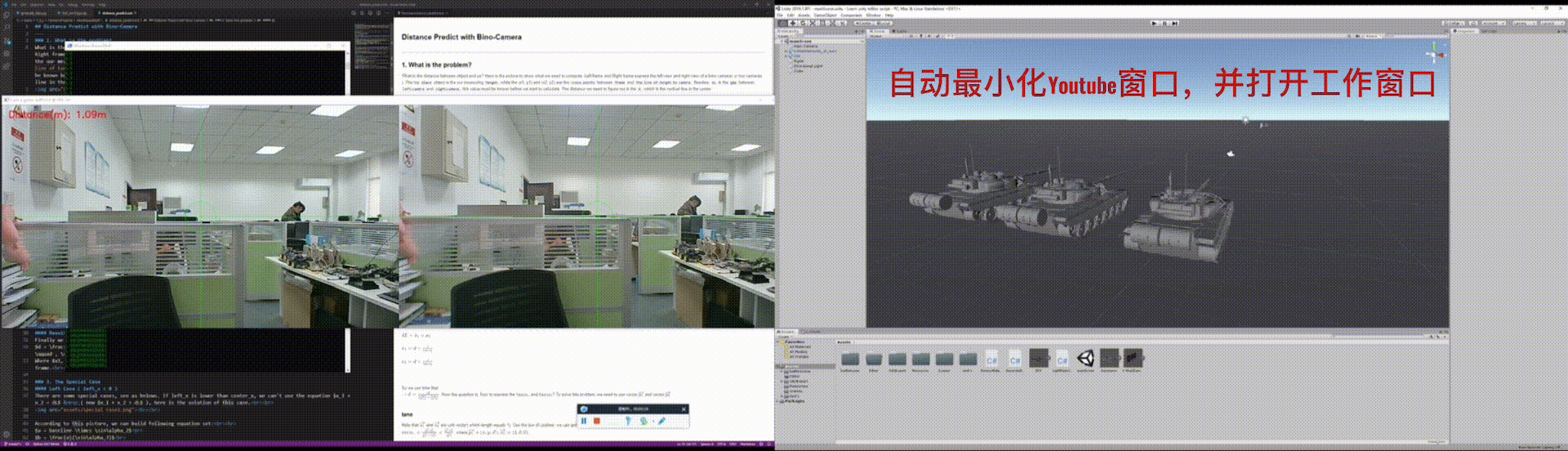
This is a demo which implements by python. Run this program while you are playing games or watching videos. When anyone comes into your camera, this program will track him and calculate the distance between your computer and that person. If the distance becomes lower than a threshold(you can change this value if you need), your game window will minimize automatically and your work-window will jump to the top of your laptop.
The key technologies of this project are face-detection and distance-predict.The face-detection skill is based on python-opencv, which named "CascadeClassifier". While the distance-predict skill is using two-view camera to get the different position (on left & right frame) of the same object and calculate the depth(See details in following chapter).
Run this program with following command, you can change the distance_threshold in the main.py. distance_threshold is the min-safe-distance, if someone walks into this distance, the Youtube will be minimized while the work-window will be set as the top window:
python main.pyNow the key problem is how to get the distance between the person and the camera? Let's see how I implement this method if you are interested about it.
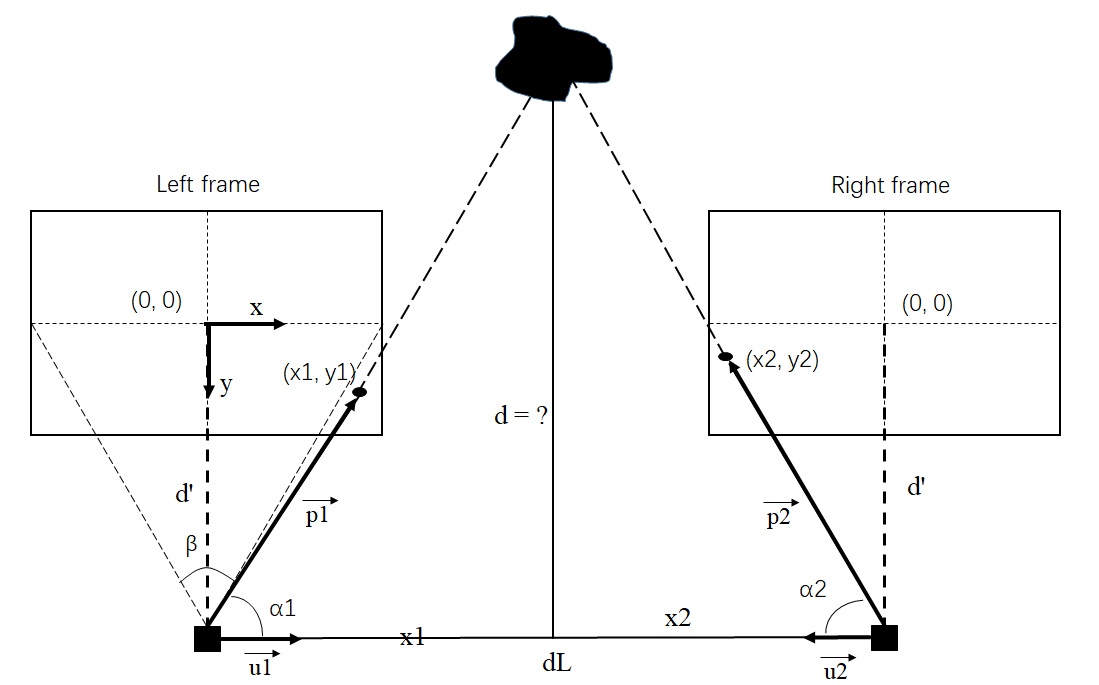
What is the distance between object and us? Here is the picture to show what we need to compute. Left frame and Right frame express the left-view and right-view of a bino-camera( or two cameras ). The top black object is the our measuring target, while the (x1, y1) and (x2, y2) are the cross points between frame and the line of target to camera. Besides, dL is the gap between left-camera and right-camera, this value must be known before we start to calculate. The distance we need to figure out is the d, which is the vertical line in the center.
Let's solve this problem now!
- dL
The dL we are already know, so we want to use this value to compute the result of d. First, we build the equation set:
$$
dL = x_1 + x_2 \
x_1 = d \times \frac{1}{\tan\alpha_1}\
x_2 = d \times \frac{1}{\tan\alpha_2}\
$$
So we can infer that:
Now the question is: how to express the
- tanα
Note that
( d' is the focal length in px, not in mm! )
Then the
$$
\cos\alpha_1 = \frac{x}{\sqrt{x^2 + y^2 + d'^2}}
$$
same as
Now we can express the
- d'
As I said, d' is the focal length in px unit, not in mm. Because we express the
- Result Finally we can draw the conclusion of d:
Where
Now we get the final equation to calculate the distance, but there are still 2 special cases we need to think about: Left case and Right case.
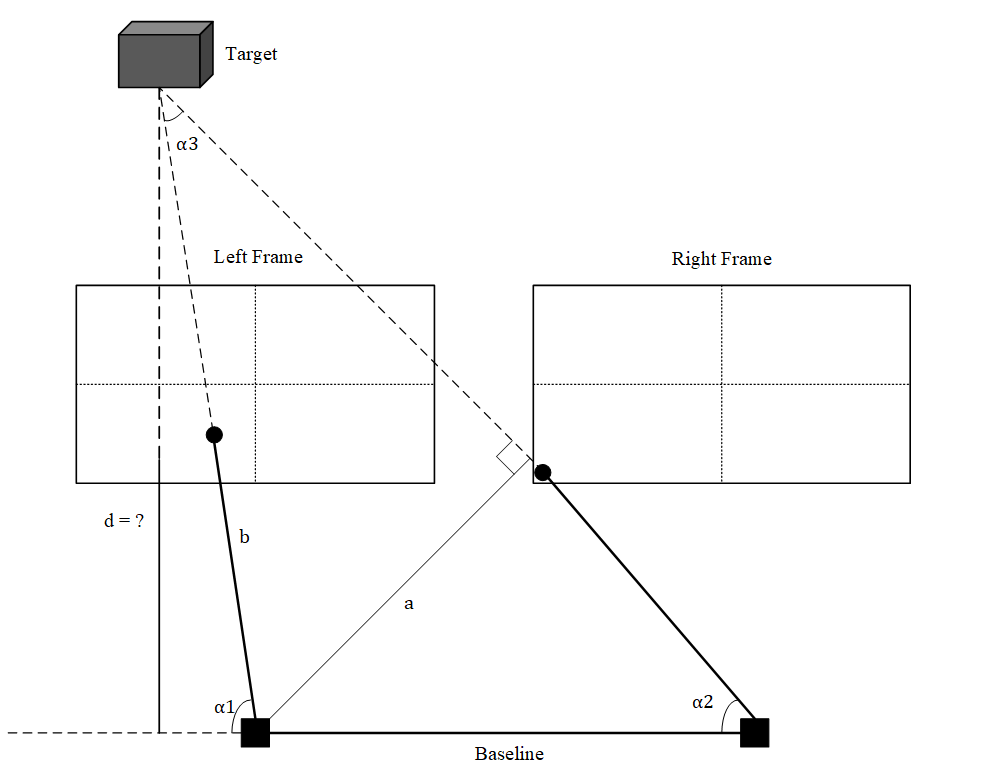
- Left Case ( left_x < 0 )
There are some special cases, see as below. If left_x is lower than center_x, we can't use the equation
According to this picture, we can build following equation set: $$ a = baseline \times \sin\alpha_2, \qquad b = \frac{a}{\sin\alpha_3}, \qquad d = b \times \sin\alpha_1 $$ which we can infer that: $$ d = \frac{baseline \times \sin\alpha_2 \times \sin\alpha_1}{\sin(\alpha_1 - \alpha_2)} $$ where: $$ \sin\alpha_3 = \sin(\alpha_1 - \alpha2),\qquad \sin\alpha_1 = \sqrt\frac{y_1^2 + d'^2}{x_1^2 + y_1^2 + d'^2}, \qquad \sin\alpha_2 = \sqrt\frac{y_2^2 + d'^2}{x_2^2 + y_2^2 + d'^2} $$
-
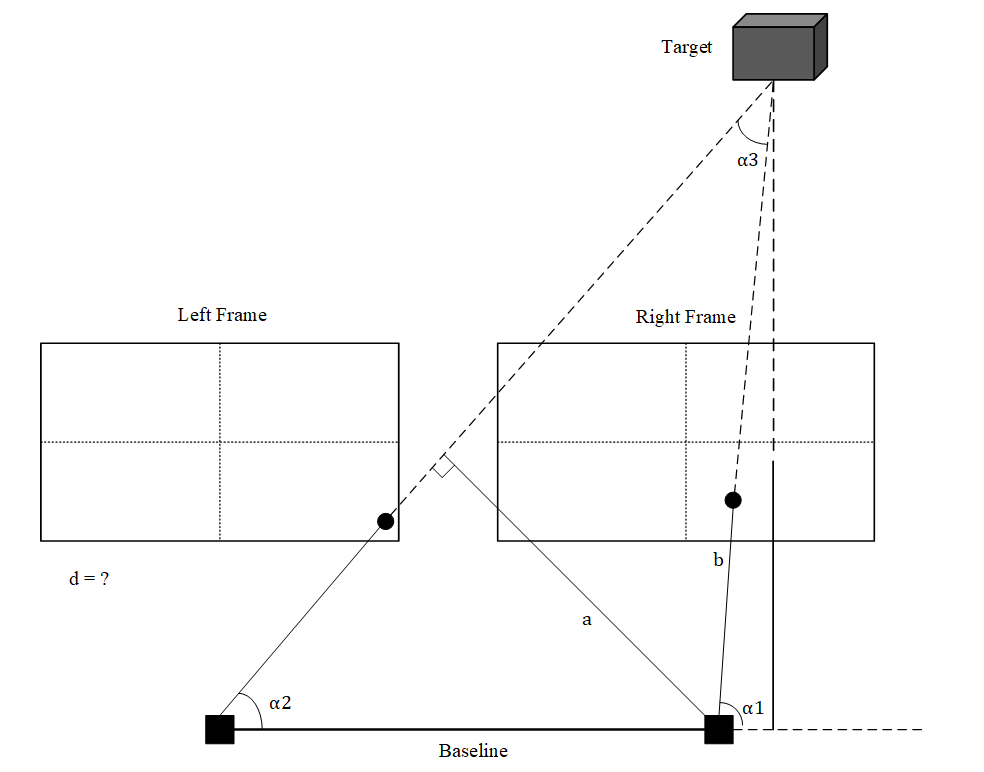
Right Case ( right_x > 0 ) The other case is the object is on the right of camera, see as below:
The main principle of solving is same as Left Case, only difference is
$\alpha_1$ and$\alpha_2$ are exchanged. $$ \sin\alpha_1 = \sqrt\frac{y_2^2 + d'^2}{x_2^2 + y_2^2 + d'^2} \ \ , \qquad \sin\alpha_1 = \sqrt\frac{y_1^2 + d'^2}{x_1^2 + y_1^2 + d'^2} $$