[TOC]
在多追一的过程中,通过设计双方不同的策略,解决追逃问题
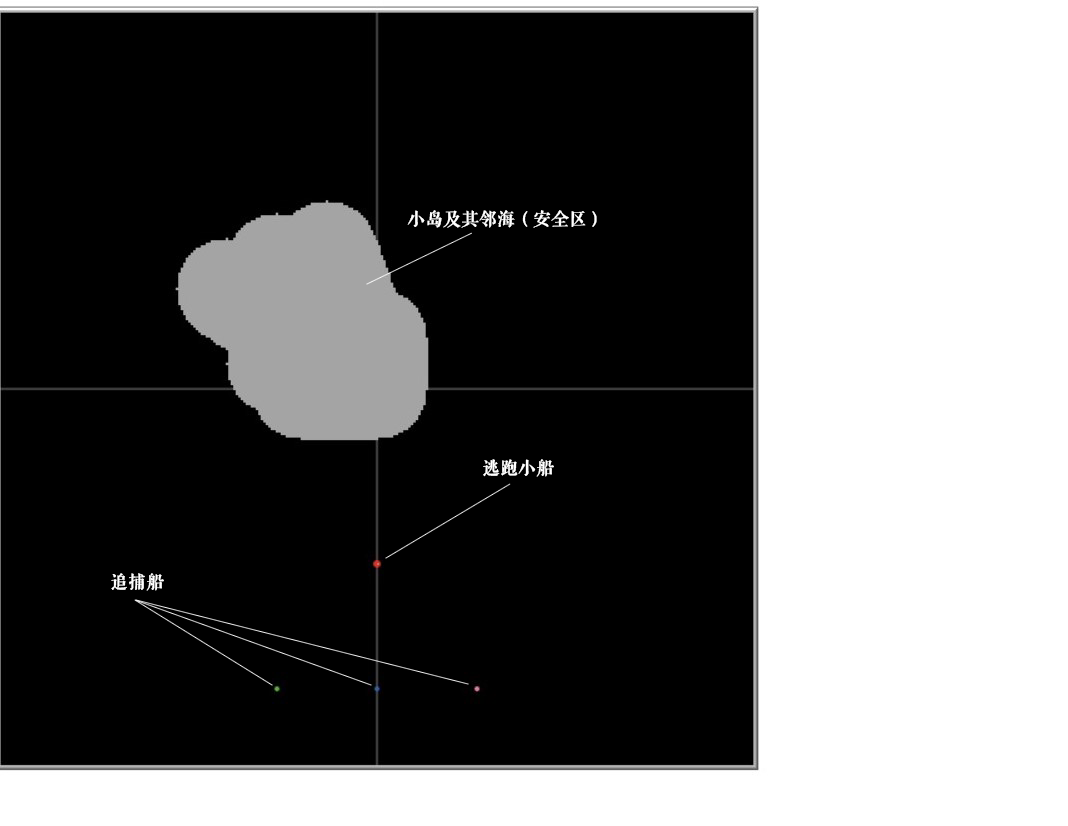
A国家派K间谍到B国家偷取情报,在K获得相关情报之后即将返回A国家,就在此时,B国家发现这一情况,开始对K进行射击,不幸的是,K的手臂被射中,在上船之后只能开启船的自动驾驶模式进行逃跑,B国家的守卫看到K已逃跑,立即派出3艘无人船进行追捕。
在A 、B国家之间 是一片海洋,这片海洋大部分是公海,但其中有一片A国家的领海(不与A国相邻),K可以进入但B国无人船无法驶入。
- 逃跑者的船与追捕者的船行驶能力不同,即追捕者船的速度更快,逃跑者的转弯能力更强,也就是说逃跑者可以在即将被追上的时候通过突然的大角度转向逃避追捕。
- 由于A国领海海底有暗礁,所以K为了自己的安全在领海的时间不能过久,在仿真中我们设置了一个计数器从逃跑开始进行计数,当K进入领海之后计数器会以两倍速度增加,不在安全区以一倍速度减少,若计数器的数值大到某一特定值即判定追捕成功。
- 当K进入自己国家领海之后B国追捕者无法知道K的具体位置
-
我们使用了Netlogo进行仿真,在仿真中,我们设置了以下参数(即图片中的各种选项,可以自己调整):
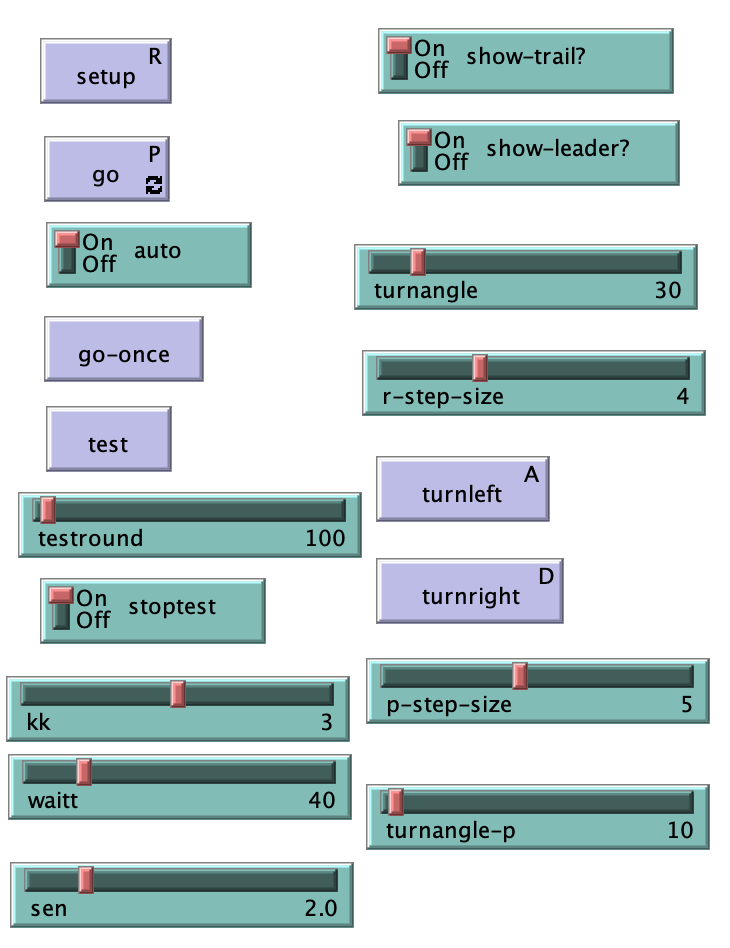
(以下说明按照从左到右,从上到下的顺序)
- setup、go:初始化与运行
- auto:选择自动驾驶还是手动驾驶
- go-once:只运行1秒
- test:运行重复仿真
- testround、stoptest:重复仿真次数与终止重复仿真
- kk、waitt:当逃跑者进入领海时,追捕者找出最佳等候位置算法的参数
- sen:逃跑者判定追捕者是否太近,要开始进行甩尾动作的参数
- show-trail:是否显示轨迹
- shoe-leader:是否显示逃跑者
- turnangle:逃跑者每秒可转动角度
- r-step-size:逃跑者每秒速度
- turnleft、turnright:手动驾驶模式下,控制逃跑者左转与右转
- p-step-size:追捕者每秒可转动角度
- turnagle-p:追捕者每秒速度
-
在我们的仿真中,假设大地图
$$150米\times150米 $$ ,逃跑者每秒可以跑 3米,转 30°;追捕者每秒可以跑 4米,转 10°。得分为逃跑者存活的秒数。
- 若自己不在安全区,且计时器的数值过大,则以一定距离绕着安全区走
- 若自己不在安全区,且计时器的数值不大,则直接找最近点进入安全区
- 若自己在安全区,且计时器的数值过大,则直接找最近点离开安全区
- 若自己在安全区,且计时器的数值不大,则在安全区内随机乱走
- 当追捕者太近时,就要采取方式甩掉他们。大致就是找到追捕者来的方向,立马往此方向的垂直方向转动。
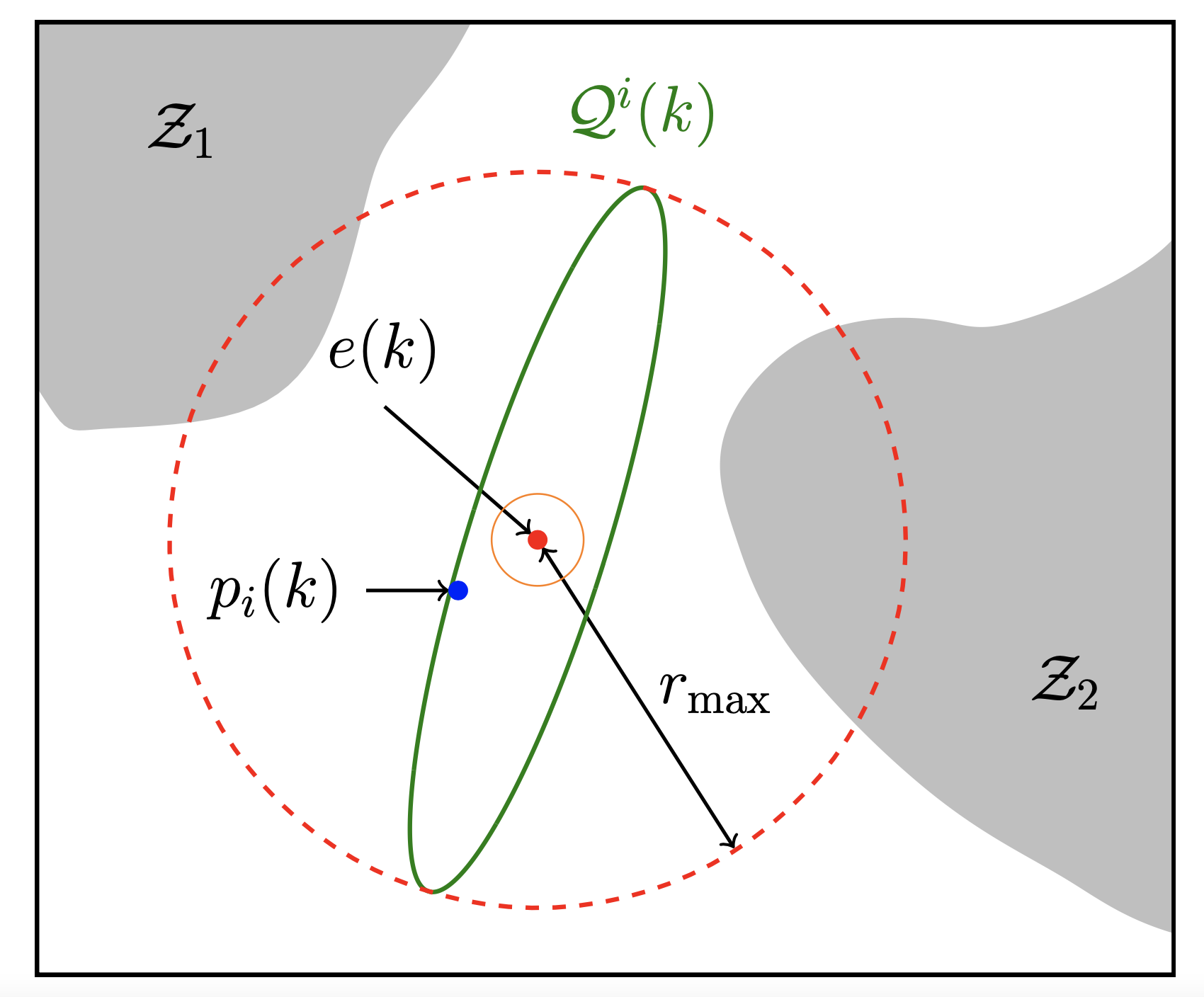
定义pi (k)与e(k)为追捕者i和逃跑者在k时刻的坐标,考虑这样一种情况,即逃跑者是静止的,并且离追踪者足够近,因此存在一个以逃跑者的位置为中心的椭球体且完全在领海之外,我们把这个椭球称为“ 安全椭球” 。 令rmin 和rmax 为安全椭球半长半短轴的上下界(如下图所示)
令$$ \upsilon_\kappa$$ ,$$\kappa=1,...,n_\upsilon$$ 为领海上距离K小于等于rmax的一组点集,对于追捕者i,定义安全椭球为:
$$
Q^i(k)\triangleq{z\in R^2|(z-e(k))^TQ_\epsilon^i(z-e(k))\leq1}
$$
此时$$Q^i(k)$$就是半定规划的解:
$$
min\ \ \ \ \ trace(Q_\epsilon^i)
\s.t.\ \ (\upsilon_\kappa-e(k))^TQ_\epsilon(\upsilon_\kappa-e(k))\geq1+\epsilon,
\(p_i(k)-e(k))^TQ_\epsilon^i(p_i(k)-e(k))\leq1-\epsilon,
\\kappa=1,...,n_\upsilon, \ \ \ \ \ \frac{1}{r^2_{max}}I\preceq Q_\epsilon^i\preceq \frac{1}{r^2_{min}}I
$$
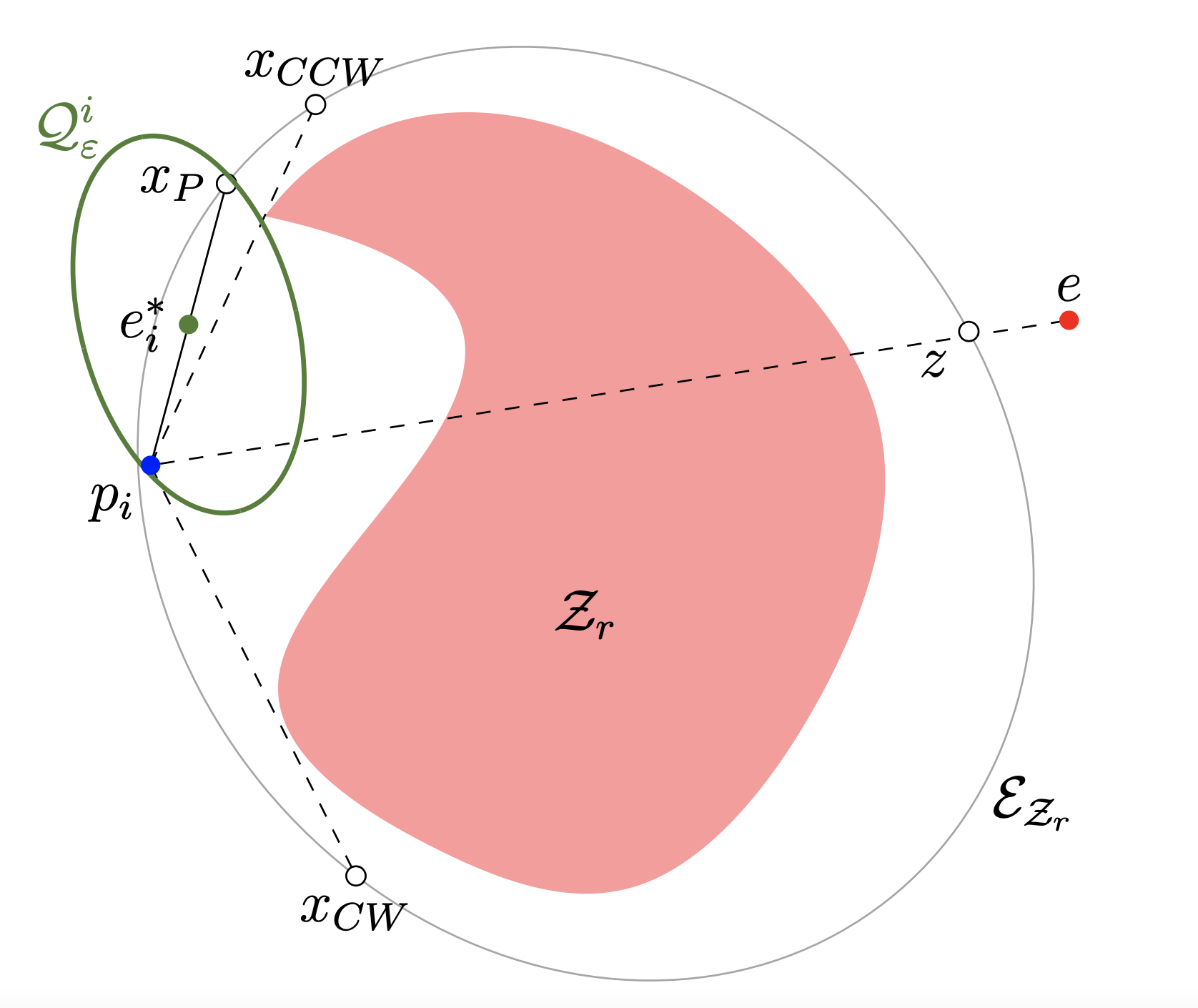
但是当追捕者和逃跑者的连线跨国领海或者二者的距离大于rmax 的时候,上面的方法就不成立了,在这种情况下,我们设定了一个虚拟追捕者,它可以使追捕者朝着逃跑者的方向运动。我们记虚拟追捕者ei^*^ 为追捕者i对应的虚拟者,定义$$\Zeta$$为领海,因为领海可能是非凸的,我们计算一个可以包含领海的体积最小的椭球$$ \epsilon_{\Zeta_r}$$ ,这个椭球距离领海最近的距离是rmin 。
令$$line(p_i,e)$$为从$$p_i$$到e的线段,定义函数$$los(p_i,e)$$在线段穿过领海为0,没穿过为1。
下面的算法判断上面的优化是否可行,如果不可行,则分配一个虚拟追逐者,并不断重复,直到最后可行。
如下图所示:
下面的算法是完整的路径规划算法:
逃跑者一旦进入领海,追踪者可能没有关于逃兵位置的可靠信息,所以追踪者根据逃兵的最大速度和它的入口点,构建一组可到达的可能位置。追击者们在禁飞区的周边安排好了自己的位置,准备在逃兵出现时将其抓获。我们采用了基于冯诺依曼的覆盖控制策略来划分逃兵的可达集,并在不进入领海的情况下,将追踪者尽可能靠近可达集的中心形Voronoi 镶嵌。
如下图所示:
对于领海Zj,q是其中的任一点,vmax 是K的最大速度,K在$$t=\tau$$时刻进入领海,进入点记为$$e(\tau)$$ ,这之后我们我们可以得到以$$v_{max}(t-\tau)$$为半径$$e(\tau)$$为圆心的圆,这个圆表示着K以最大速度逃跑的可达范围,我们定义这个圆与领海的重合部分为$$R_j(t,\tau,v_\max)$$, 也就是说K一定在这个范围里,即:
$$
R_j(t,\tau,v_\max)=\Beta(e(\tau),v_\max(t-\tau))\bigcap\Z_j
$$
同时定义函数$$\rho$$:
$$
\rho(q,t)=\begin{equation}
\left{
\begin{array}{l}
1,if\ \ q\in\ R_j(t,\tau,v_\max),\
0,otherwise.\
\end{array}
\right.
\end{equation}
$$
如果追踪者可以在禁飞区内自由移动,我们会想要分配追踪者到任何可能的位置的平均距离最小化。
令$$\overline{p_i}$$是追捕者的目标位置,定义基于这些目标位置的可达集Rj 的Voronoi 镶嵌:
$$
V_i={q\in R_j|\ \ \left|q-\overline{p_i}\right|^2\leq \left|q-\overline{p_k}\right|^2,k=1,2,...,n_p}
$$
在此基础上,我们定义一个捕获成本:
$$
\nu(\overline{p_1},...,\overline{p_n})=\sum_{i=1}^{n_p}\int_{V_i}\left|q-\overline{p_i}\right|^2\rho(q,t)dq
$$
我们可以看出,$$\nu$$越小则越容易追捕。
我们定义Voronoi镶嵌的质量和质心: $$ M_{V_i}=\int_{V_i}\rho(q,t)dq, \ \ \ C_{V_i}=\frac{1}{M_{V_i}}\int_{V_i}q\rho(q,t)dq $$ 上面的捕获成本是对于虚拟追捕者而言的,考虑到我们的追踪者必须留在禁飞区之外,我们必须调整移动到重心的算法来适应这种受限的情况。在此时,对于虚拟追捕者$$\overline{p_i}$$而言, 定义真正的追捕者$$p_i=\overline{p_i}+d_i$$ ,那么我们可以定义真正的捕获函数: $$ H(d_1,...,d_n)=\sum_{i=1}^{n_p}\int_{V_i}\left|q-\overline{p_i}-d_i\right|^2\rho(q,t)dq $$ 其中$$\overline{p_i}=C_{V_i}$$,同时我们的问题就化为了以下的优化问题: $$ \min \limits_{(d_1,...,d_n)}\ H(d_1,...,d_n) \s.t.\ \ \ \ d_i+\overline{p_i}\notin\Z_j $$ 通过求解此优化问题可以得到如下的路径规划算法:
我们使用Netlogo软件进行仿真
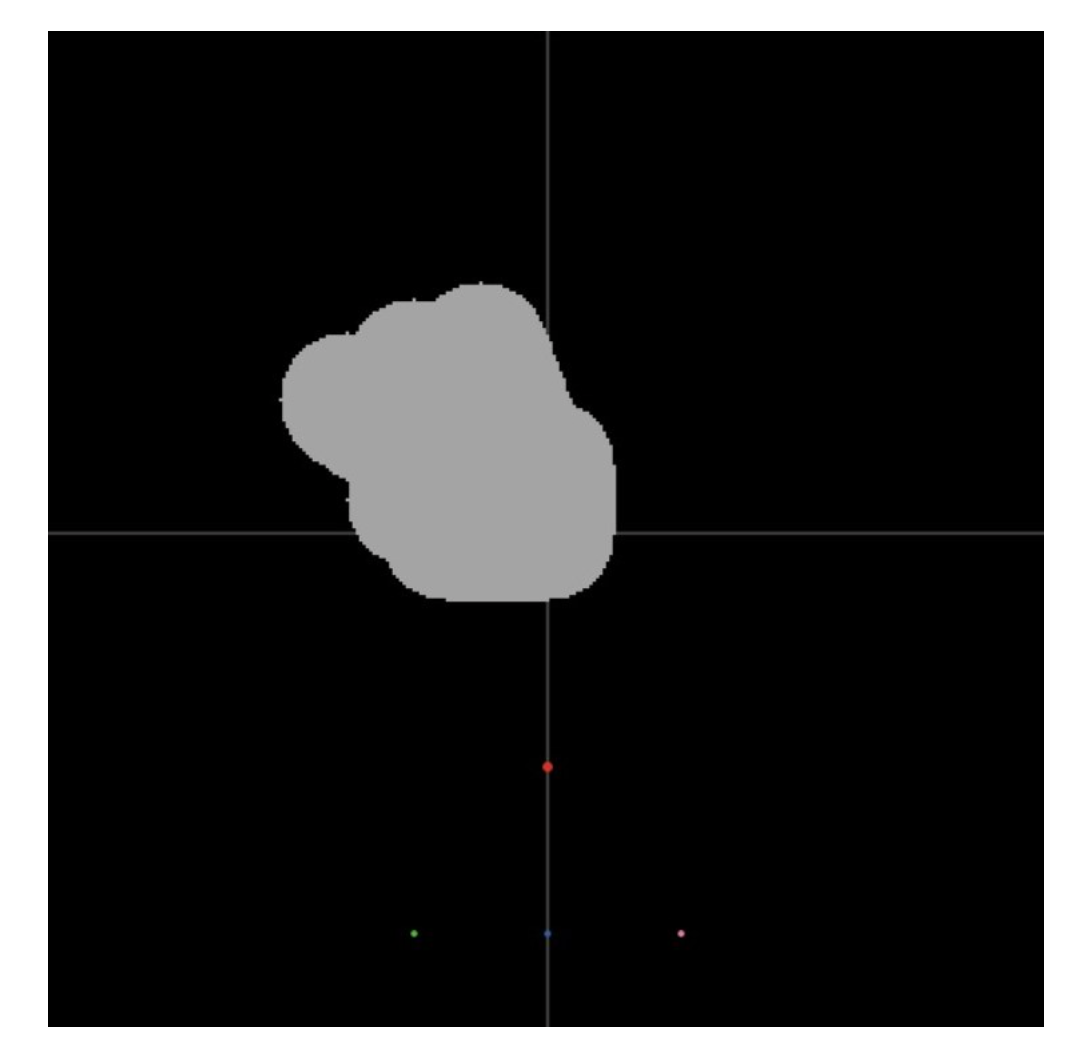
- 首先进行初始化
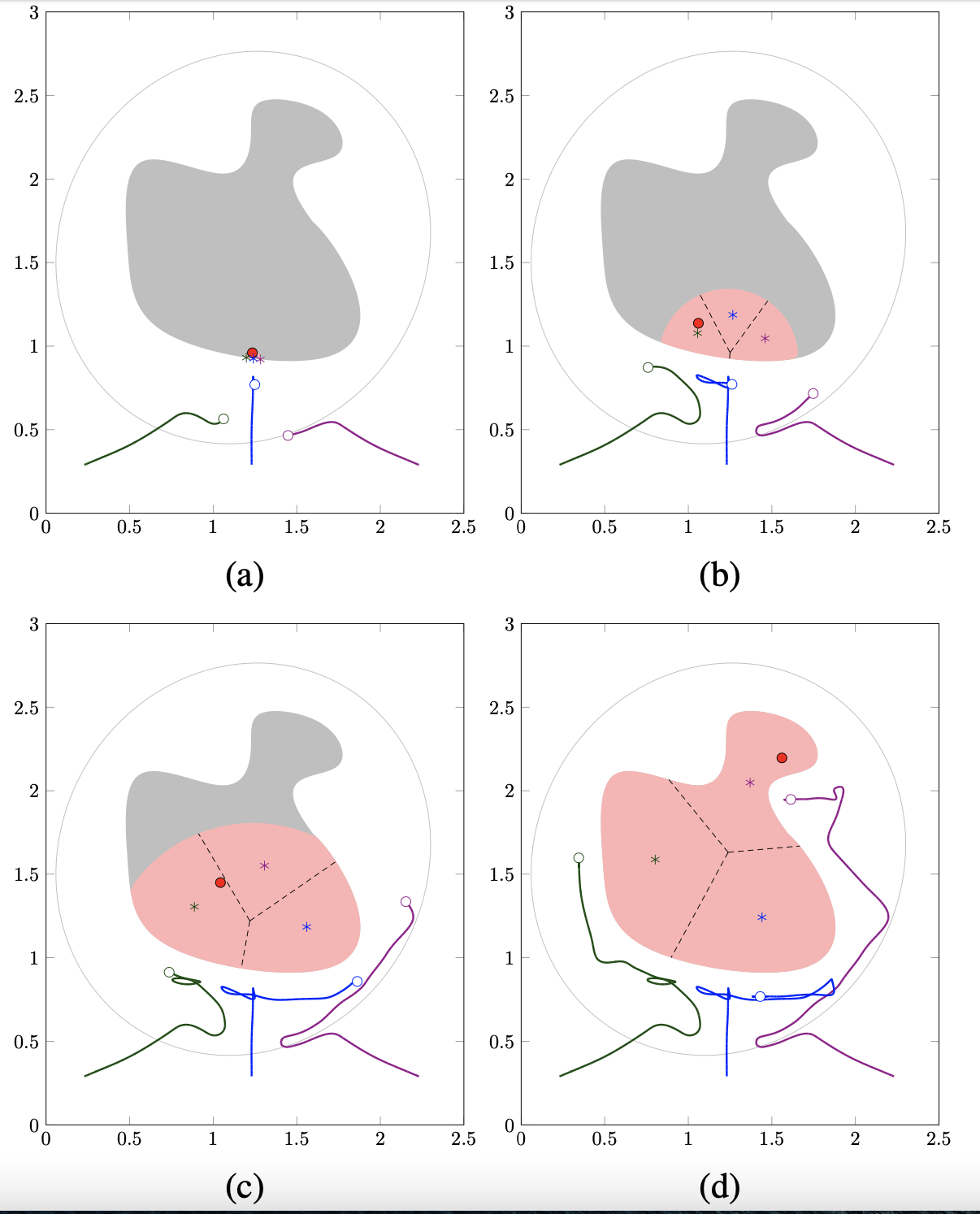
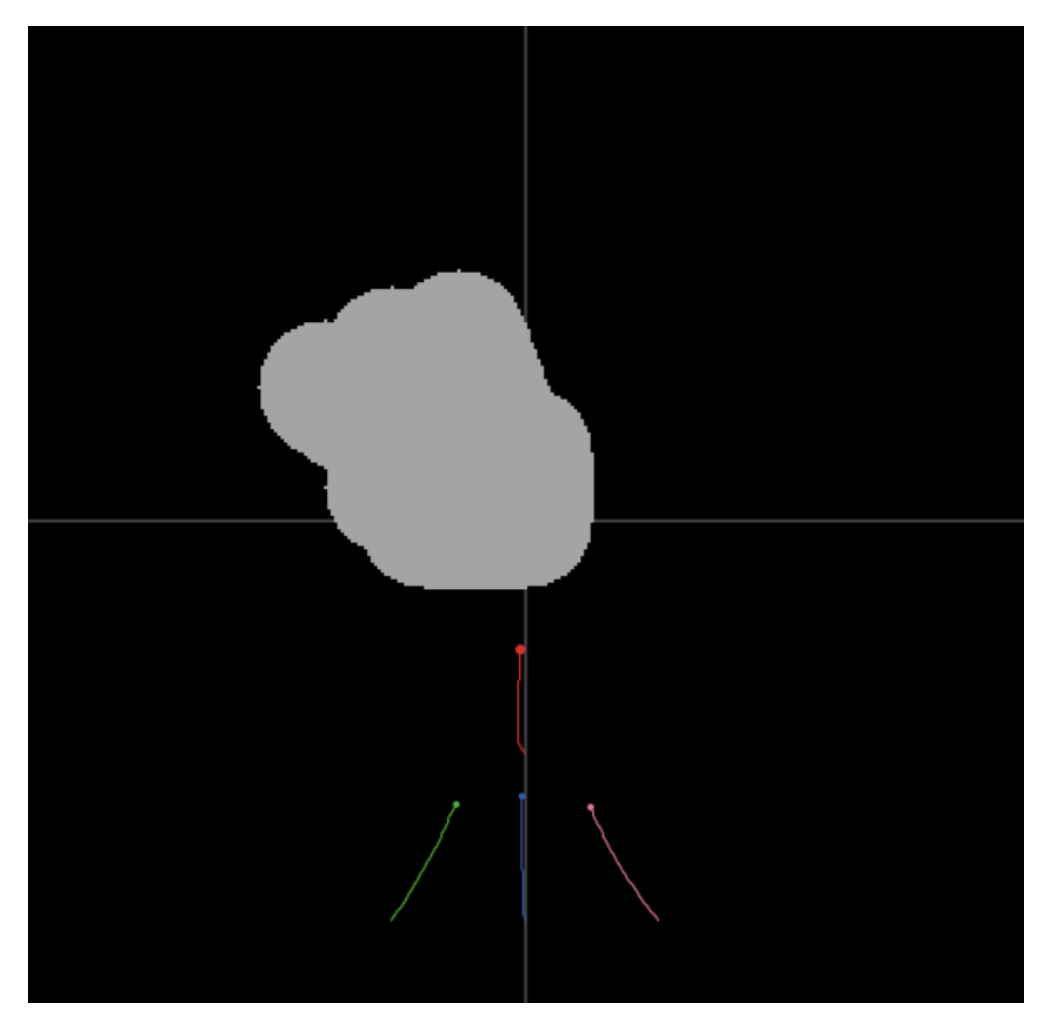
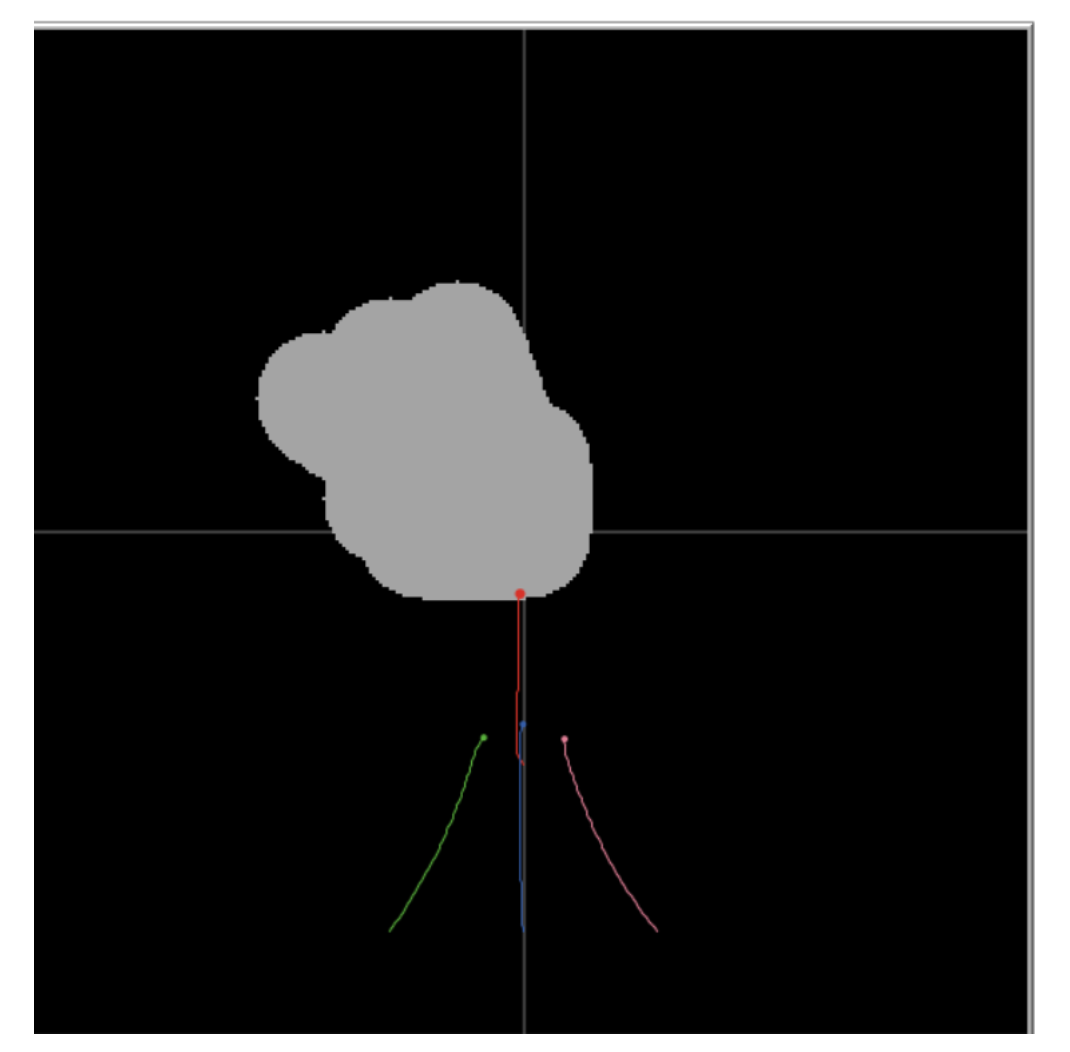
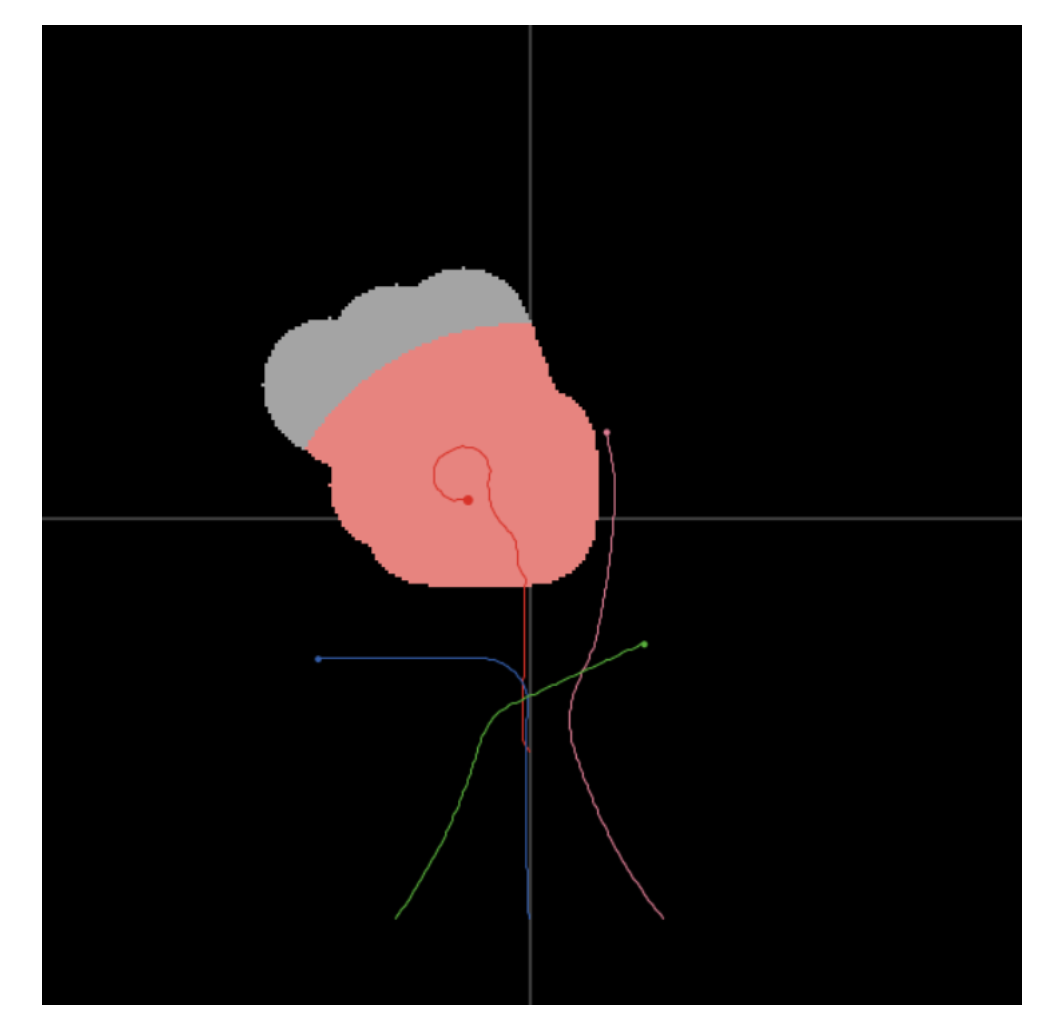
- 然后开始运行:
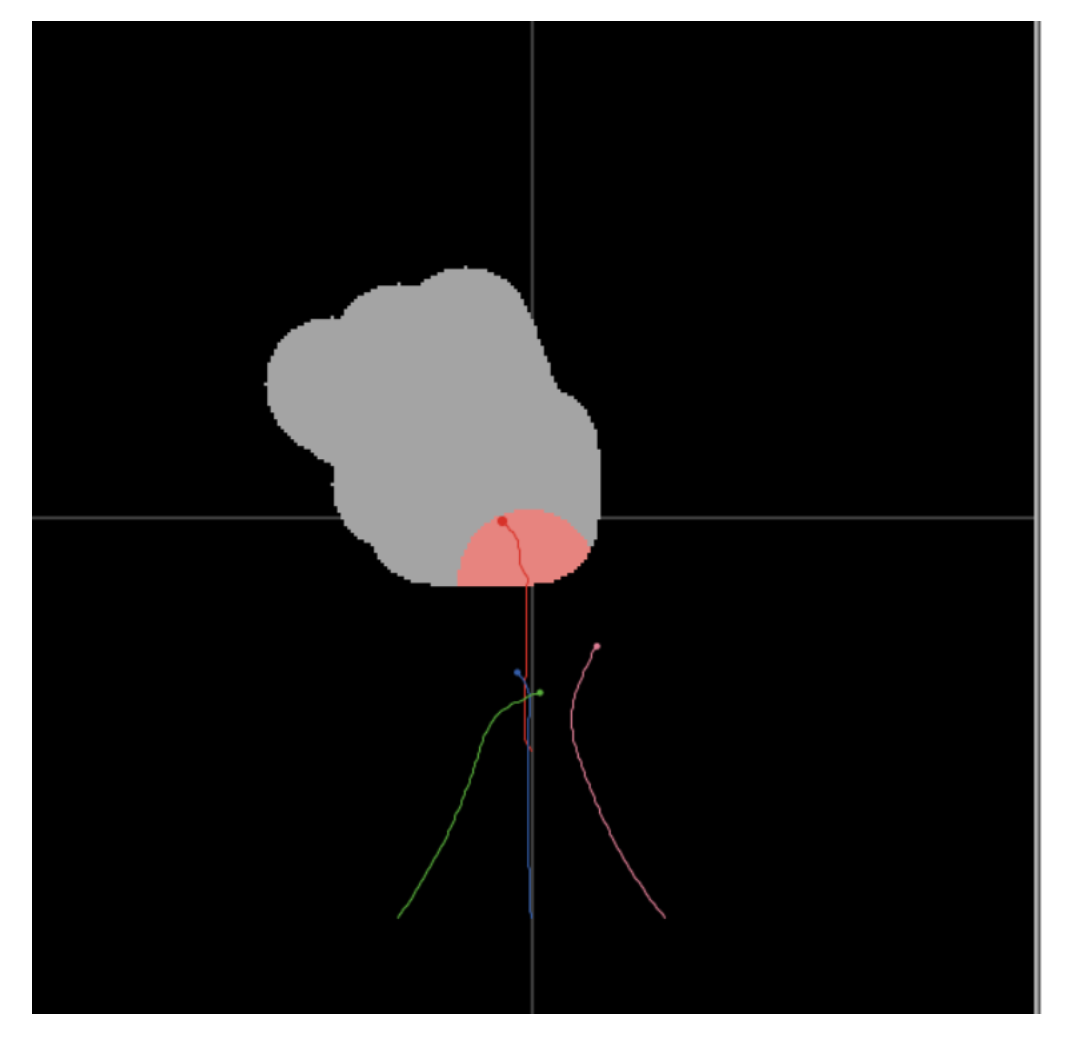
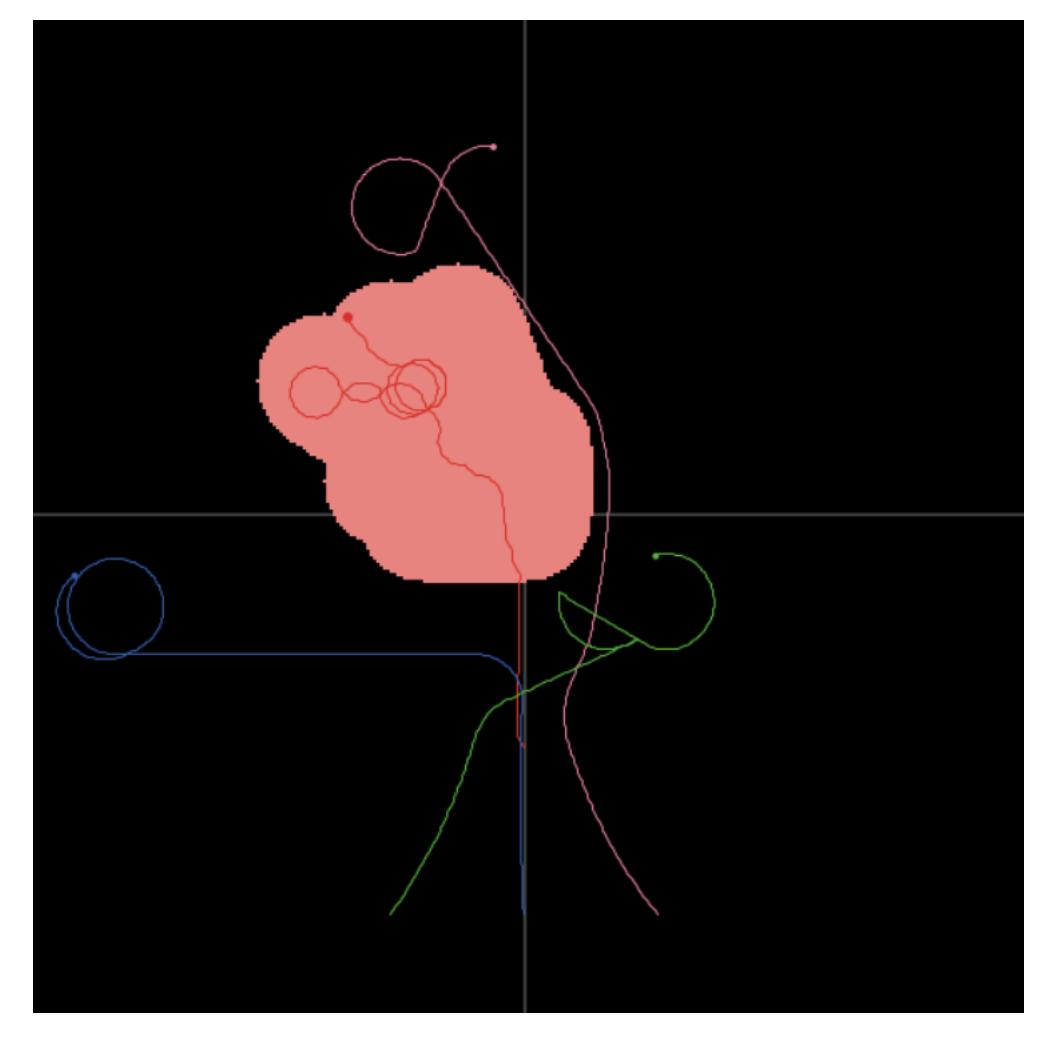
- 逃跑者进入领海:
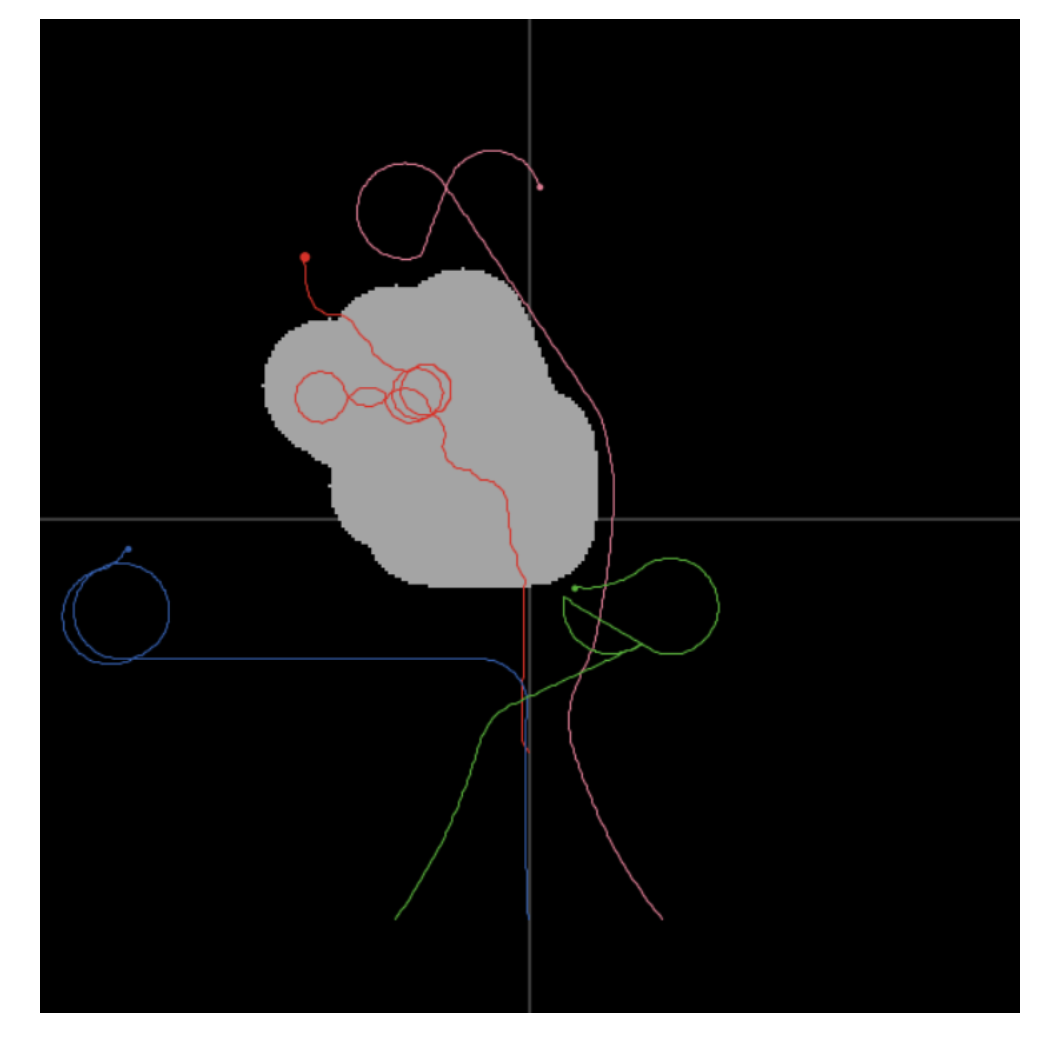
- 即将出领海
- 在公海继续追捕:
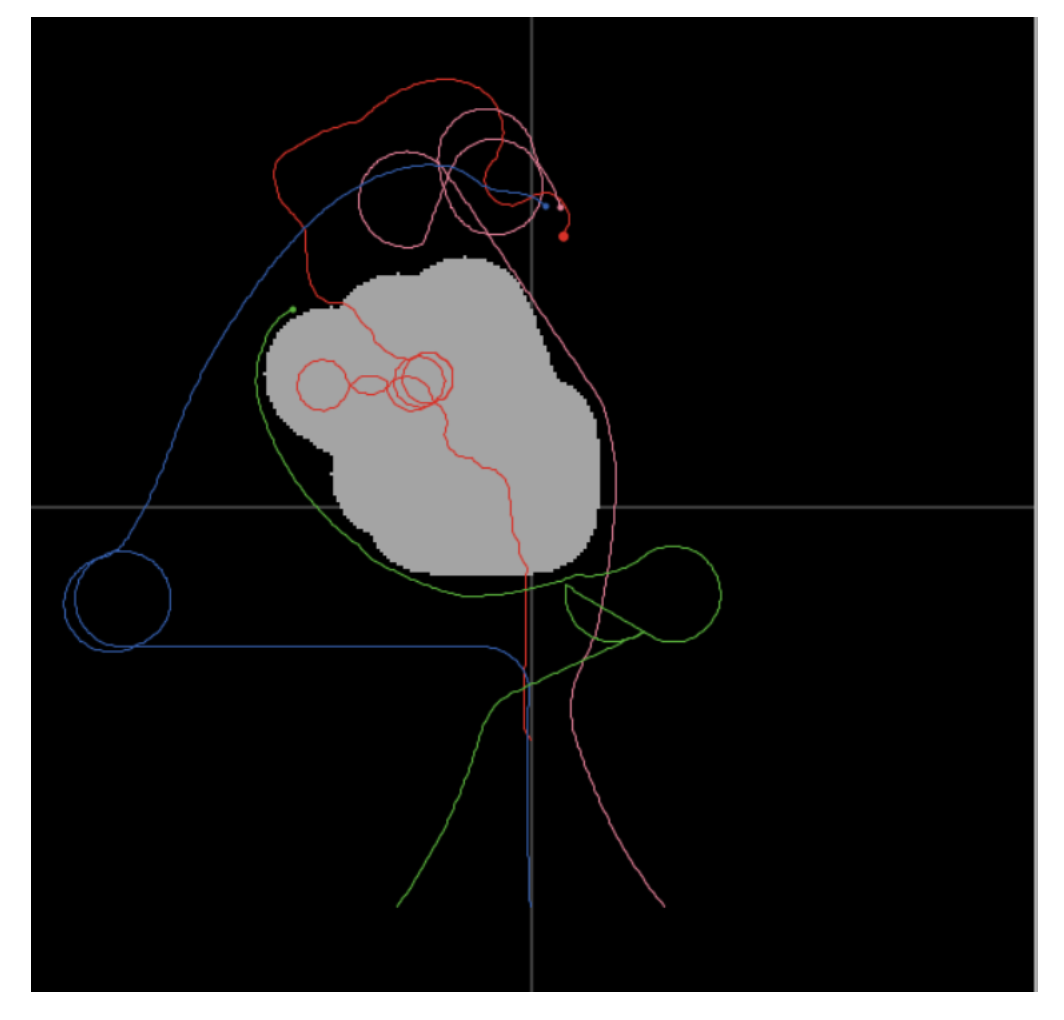
- 追捕成功
- 此外,我们还进行了200次的尝试,得到以下结果:
逃跑者的得分最高为1588,平均得分约为269