Optimal Stopping via Randomized Neural Networks

This repository is the official implementation of the paper Optimal Stopping via Randomized Neural Networks.

Installation

Clone this git repo and cd into it.

git clone https://github.com/HeKrRuTe/OptStopRandNN.git
cd OptStopRandNN

Then create a new environment and install all dependencies and this repo.

with conda:

conda create --name OptStopRandNN python=3.7
conda activate OptStopRandNN
pip install --upgrade --no-cache-dir -e .

with virtualenv, use equivalent command for non debian based systems.

sudo apt-get install python3-venv
python3 -m venv py3
source py3/bin/activate
pip3.7 install --no-cache-dir -e .

That's all!

List of the algorithms available in Optimal Stopping Library

Finite Differences
- binomial: binomial tree.
Backward Induction
- LSM: Least Square Monte Carlo. (Longstaff and Schwartz, 2001)
- NLSM: Neural Least Square Monte Carlo. (Lapeyre and Lelong, 2019) (Becker, Cheridito and Jentzen, 2019)
- DOS: Deep Optimal Stopping. (Becker, Cheridito and Jentzen, 2019)
- RLSM: Randomized Least Square Monte Carlo. (Herrera, Krach, Ruyssen and Teichmann 2021)
- RRLSM: Randomized Recurrent Least Square Monte Carlo. (Herrera, Krach, Ruyssen and Teichmann 2021)
Reinforcement Learning
- FQI: fitted Q-Iteration. (Tsitsiklis and Van Roy, 2001) (Li, Szepesvari and Schuurmans, 2009)
- LSPI: least-squares policy iteration. (Li, Szepesvari and Schuurmans, 2009)
- RFQI: randomized fitted Q-Iteration. (Herrera, Krach, Ruyssen and Teichmann 2021)

Running the algorithms

First cd into "OptStopRandNN". Then activate the virtual environmant:

with conda

conda activate OptStopRandNN

with virtualenv

source py3/bin/activate

Some usage info

Specify number of parallel jobs (i.e. CPUs that are used parallelly to run multiple algorithms) by replacing N by the wanted number of CPUs. By default, it uses all but one available CPUs.

python optimal_stopping/run/run_algo.py --nb_jobs=N --configs=...

Note: ... needs to be replaced by a string which is the name of a parameter configuration defined in configs.py. New parameter configurations can be defined there for usage.

Generate tables directly:

python optimal_stopping/run/run_algo.py --generate_pdf=True --configs=...

Write comparison tables and figures used in PDF:

python optimal_stopping/run/write_figures.py --configs=single_test_maxcall_10stocks

Profiling performances:

python3 -m cProfile optimal_stopping/run/run_algo.py   --algo=longstaffSchwartz   --stock_model=BlackScholes   --strike
=100   --volatility=0.3   --spot=100   --rate=0.02   --dividend=0.0   --maturity=1   --nb_stocks=1   
--nb_paths=1000   --nb_steps=100   --payoff=MaxPut   --output_dir=output

Overview of Flags for optimal_stopping/run/run_algo.py:

configs: list of config names to run
nb_jobs: int, the number of parallel runs
print_errors: debugging mode
path_gen_seed: seed for path generation, default: None (-> using random seed)
compute_upper_bound: compute upper bound for the price

The Markovian Case

Max call option on Black Scholes for different number of stocks d and varying initial stock price x0. RLSM achieves the highest prices while being the fastest and having considerably less trainable parameters.

Generate tables of paper:

python optimal_stopping/run/run_algo.py --configs="table_spots_Dim_BS_MaxCallr0","table_Dim_Heston_MaxCallr0","table_spots_Dim_BS_MaxCallr0_do","table_Dim_Heston_MaxCallr0_do","table_spots_Dim_BS_MaxCallr0_bf","table_Dim_Heston_MaxCallr0_bf","table_smallDim_BS_GeoPut","table_Dim_BS_BasktCallr0","table_Dim_BS_BasktCallr0_bf","table_manyDates_BS_MaxCallr0_1","table_manyDates_BS_MaxCallr0_2","table_spots_Dim_MaxCallr0_ref","table_spots_Dim_BasktCallr0_ref","table_manyDates_BS_MaxCallr0_ref" --nb_jobs=10;
python optimal_stopping/run/write_figures.py --configs="table_spots_Dim_BS_MaxCallr0_gt1","table_Dim_Heston_MaxCallr0_gt1","table_BasketCall_payoffsr0_gt1","table_manyDates_BS_MaxCallr0_gt1";
python optimal_stopping/run/write_figures.py --configs="table_GeoPut_payoffs_gt1" --rm_from_index="volatility","dividend","nb_dates";
python optimal_stopping/utilities/plot_tables.py --configs="table_spots_Dim_BS_MaxCallr0_gt1","table_Dim_Heston_MaxCallr0_gt1","table_BasketCall_payoffsr0_gt1","table_GeoPut_payoffs_gt1","table_manyDates_BS_MaxCallr0_gt1";

# true price for GeoPut
python optimal_stopping/run/run_algo.py --configs="table_smallDim_BS_GeoPut_ref1","table_smallDim_BS_GeoPut_ref2","table_smallDim_BS_GeoPut_ref3","table_smallDim_BS_GeoPut_ref4","table_smallDim_BS_GeoPut_ref5","table_smallDim_BS_GeoPut_ref6","table_smallDim_BS_GeoPut_ref7","table_smallDim_BS_GeoPut_ref8","table_smallDim_BS_GeoPut_ref9" --nb_jobs=10;

# RoughHeston
python optimal_stopping/run/run_algo.py --configs="table_Dim_RoughHeston_MaxCallr0","table_Dim_RoughHeston_MaxCallr0_do","table_Dim_RoughHeston_MaxCallr0_bf","table_Dim_RoughHeston_MaxCallr0_RRLSM" --nb_jobs=10;
python optimal_stopping/run/write_figures.py --configs="table_Dim_RoughHeston_MaxCallr0_gt" --rm_from_index="factors";
python optimal_stopping/run/write_figures.py --configs="table_Dim_RoughHeston_MaxCallr0_gt1" --rm_from_index="factors";
python optimal_stopping/utilities/plot_tables.py --configs="table_Dim_RoughHeston_MaxCallr0_gt1"

# MinPut
python optimal_stopping/run/run_algo.py --configs="table_spots_Dim_BS_MinPut","table_spots_Dim_BS_MinPut_do","table_spots_Dim_BS_MinPut_bf" --nb_jobs=10;
python optimal_stopping/run/write_figures.py --configs="table_spots_Dim_BS_MinPut_gt1"
python optimal_stopping/utilities/plot_tables.py --configs="table_spots_Dim_BS_MinPut_gt1"

# MaxCall with dividend
python optimal_stopping/run/run_algo.py --configs="table_Dim_BS_MaxCall_div","table_Dim_BS_MaxCall_div_bf" --nb_jobs=10;
python optimal_stopping/run/write_figures.py --configs="table_Dim_BS_MaxCall_div_gt1";
python optimal_stopping/utilities/plot_tables.py --configs="table_Dim_BS_MaxCall_div_gt1";

# MaxCall with dividend many dates
python optimal_stopping/run/run_algo.py --configs="table_manyDates_BS_MaxCall_div_1","table_manyDates_BS_MaxCall_div_FQI","table_manyDates_BS_MaxCall_div_2","table_manyDates_BS_MaxCall_div_FQI_2" --nb_jobs=2;
python optimal_stopping/run/write_figures.py --configs="table_manyDates_BS_MaxCall_div_gt1";
python optimal_stopping/utilities/plot_tables.py --configs="table_manyDates_BS_MaxCall_div_gt1";

# MinPut Heston
python optimal_stopping/run/run_algo.py --configs="table_spots_Dim_Heston_MinPut","table_spots_Dim_Heston_MinPut_bf" --nb_jobs=10;
python optimal_stopping/run/write_figures.py --configs="table_spots_Dim_Heston_MinPut_gt1"
python optimal_stopping/utilities/plot_tables.py --configs="table_spots_Dim_Heston_MinPut_gt1"

# MaxCall with dividend Heston
python optimal_stopping/run/run_algo.py --configs="table_Dim_Heston_MaxCall_div","table_Dim_Heston_MaxCall_div_bf" --nb_jobs=10;
python optimal_stopping/run/write_figures.py --configs="table_Dim_Heston_MaxCall_div_gt","table_Dim_Heston_MaxCall_div_gt1";
python optimal_stopping/utilities/plot_tables.py --configs="table_Dim_Heston_MaxCall_div_gt1";

Tables of (rough) Heston with variance:

# MaxCall
python optimal_stopping/run/run_algo.py --configs="table_Dim_HestonV_MaxCallr0","table_Dim_HestonV_MaxCallr0_bf","table_spots_Dim_HestonV_MaxCallr0_ref" --nb_jobs=10;
python optimal_stopping/run/write_figures.py --configs="table_Dim_HestonV_MaxCallr0_gt","table_Dim_HestonV_MaxCallr0_gt1";
python optimal_stopping/utilities/plot_tables.py --configs="table_Dim_HestonV_MaxCallr0_gt1"

# GeoPut
python optimal_stopping/run/run_algo.py --configs="table_smallDim_HestonV_GeoPut" --nb_jobs=10;
python optimal_stopping/run/write_figures.py --configs="table_GeoPut_HestonV_payoffs_gt","table_GeoPut_HestonV_payoffs_gt1";
python optimal_stopping/utilities/plot_tables.py --configs="table_GeoPut_HestonV_payoffs_gt1"

# MinPut
python optimal_stopping/run/run_algo.py --configs="table_spots_Dim_HestonV_MinPut","table_spots_Dim_HestonV_MinPut_bf" --nb_jobs=10;
python optimal_stopping/run/write_figures.py --configs="table_spots_Dim_HestonV_MinPut_gt1";
python optimal_stopping/utilities/plot_tables.py --configs="table_spots_Dim_HestonV_MinPut_gt1"

# MaxCall Dividend
python optimal_stopping/run/run_algo.py --configs="table_Dim_HestonV_MaxCall_div","table_Dim_HestonV_MaxCall_div_bf" --nb_jobs=10;
python optimal_stopping/run/write_figures.py --configs="table_Dim_HestonV_MaxCall_div_gt1";
python optimal_stopping/utilities/plot_tables.py --configs="table_Dim_HestonV_MaxCall_div_gt1"

# RoughHeston
python optimal_stopping/run/run_algo.py --configs="table_Dim_RoughHestonV_MaxCall","table_Dim_RoughHestonV_MaxCall_dopath","table_Dim_RoughHestonV_MaxCall_bf","table_Dim_RoughHestonV_MaxCall_RRLSM" --nb_jobs=10;
python optimal_stopping/run/write_figures.py --configs="table_Dim_RoughHestonV_MaxCall_gt" --rm_from_index="factors","use_path";
python optimal_stopping/run/write_figures.py --configs="table_Dim_RoughHestonV_MaxCall_gt1" --rm_from_index="factors","use_path";
python optimal_stopping/utilities/plot_tables.py --configs="table_Dim_RoughHestonV_MaxCall_gt1"

Empirical Convergence studies:

Mean and standard deviation (bars) of the price for a max-call on 5 stocks following for the Heston model (down) for RLSM (right) and RFQI (left) for varying the number of paths and varying for RLSM the number of neurones in the hidden layer.

Generate convergence studies of the paper:

python optimal_stopping/run/run_algo.py --configs=table_conv_study_Heston_LND --nb_jobs=80 --generate_pdf;
python optimal_stopping/run/run_algo.py --configs=table_conv_study_BS_LND --nb_jobs=80 --generate_pdf;
python optimal_stopping/run/run_algo.py --configs=table_conv_study_Heston_FQIR --nb_jobs=80 --generate_pdf;
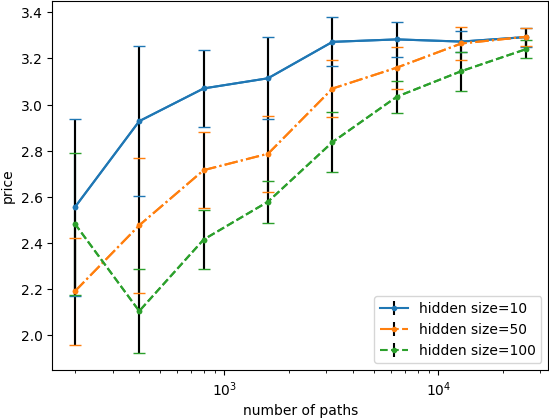
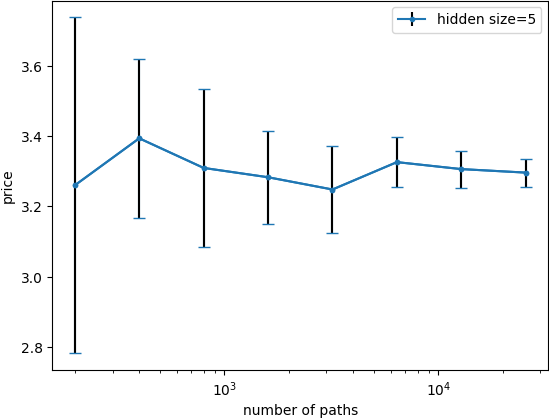
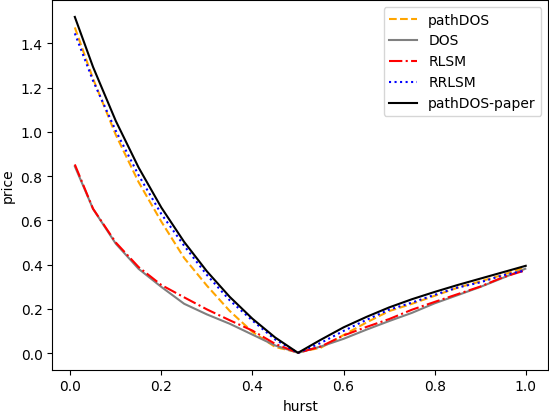
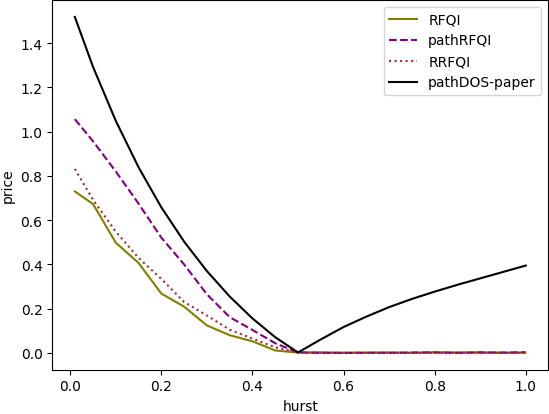
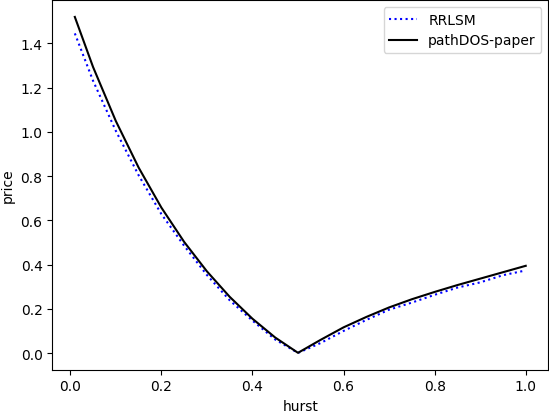
python optimal_stopping/run/run_algo.py --configs=table_conv_study_BS_FQIR --nb_jobs=80 --generate_pdf;

The Non-Markovian Case: a fractional Brownian Motion

Left: algorithms processing path information outperform. Middle: reinforcement learning algorithms do not work well in non-Markovian case. Right: RRLSM achieves similar results as reported in [(Becker, Cheridito and Jentzen, 2019)](https://arxiv.org/abs/1912.11060), while using only 20K paths instead of 4M for training wich took only 4s instead of the reported 430s.

Generate the hurst plot of the paper:

python optimal_stopping/run/run_algo.py --configs=table_RNN_DOS --nb_jobs=10;
python optimal_stopping/run/run_algo.py --configs=table_RNN_DOS_PD --nb_jobs=10;
python optimal_stopping/run/run_algo.py --configs=table_RNN_DOS_bf --nb_jobs=10;
python optimal_stopping/run/run_algo.py --configs=table_RNN_DOS_randRNN --nb_jobs=10;
python optimal_stopping/run/run_algo.py --configs=table_RNN_DOS_FQIR_PD --nb_jobs=10;
python optimal_stopping/run/run_algo.py --configs=table_RNN_DOS_FQIRRNN --nb_jobs=10;
python optimal_stopping/utilities/plot_hurst.py;

Generate the hurst table of the paper:

python optimal_stopping/run/run_algo.py --configs=table_highdim_hurst0 --nb_jobs=10;
python optimal_stopping/run/run_algo.py --configs=table_highdim_hurst_PD0 --nb_jobs=10;
python optimal_stopping/run/run_algo.py --configs=table_highdim_hurst_RNN0 --nb_jobs=10;
python optimal_stopping/run/run_algo.py --configs="table_highdim_hurst","table_highdim_hurst_PD","table_highdim_hurst_RNN" --nb_jobs=10;
python optimal_stopping/run/write_figures.py --configs=table_highdim_hurst_gt --rm_from_index="factors","use_path";

Generate the Ridge Regression Tests:

python optimal_stopping/run/run_algo.py --configs=table_Ridge_MaxCall --nb_jobs=10;
python optimal_stopping/run/write_figures.py --configs=table_Ridge_MaxCall;

Generate the other basis functions Tests:

python optimal_stopping/run/run_algo.py --configs=table_OtherBasis_MaxCall --nb_jobs=10;
python optimal_stopping/run/write_figures.py --configs=table_OtherBasis_MaxCall;

Compute Lower and Upper bounds:

python optimal_stopping/run/run_algo.py --configs=table_price_lower_upper_1 --compute_upper_bound --nb_jobs=10;

Compute Greeks (and price):

Currently, the Greeks: delta, gamma, theta, rho and vega are supported. For the computation of delta and gamma, there are multiple computation possibilities, since the computation of gamma (as 2nd derivative) tends to be unstable. The different possibilities are:

central, forward, backward finite difference (FD) method for delta and the respective 2nd order FD method for gamma. this is unstable for gamma (didn't produce good results in any of our tests) and is therefore not recommended.
central, forward, backward finite difference (FD) method for delta and computation of gamma via the Black-Scholes PDE. This gives good results, if theta is computed well (which is the case for all methods). This method is currently restricted to the case of a underlying Black-Scholes model.
both of the above methods can be computed either with or without freezing the execution boundary. We recommend to use fd_freeze_exe_boundary=True, since it stabilizes the results. Moreover, the epsilon for the FD method can be chosen (recommended eps=1e-9).
the regression based method (see the "naive method" (Section 3.1) in Simulated Greeks for American Options). This method is very stable. Here epsilon (the standard deviation of the distortion term) and the degree of the polynomial basis for regression have to be chosen (recommended eps=5, poly_deg=2).

The greeks theta, rho, vega are always computed via central FD method, since there are no stability issues. Also here, the epsilon is controlled with eps, together with the epsilon for the FD method for delta and gamma. For the binomial model, we recommend eps=1e-9.

Overview of flags specific to greeks computation:

compute_greeks: whether to compute greeks or do pricing only
greeks_method: one of {"central", "forward", "backward", "regression"}
fd_compute_gamma_via_PDE: whether to use Black-Scholes PDE to compute gamma. only works if model="BlackScholes".
eps: the epsilon for the FD method or the standard deviation of the distortion term in the regression method.
fd_freeze_exe_boundary: whether to use the central execution boundary for the upper and lower term also when computing delta.
poly_deg: the degree of the polynomial used in the regression method

Generate the greeks table of the paper:

Via (central) finite difference (FD) method:

python optimal_stopping/run/run_algo.py --configs=table_greeks_1,table_greeks_1_2 --nb_jobs=1 --compute_greeks=True --greeks_method="central" --fd_compute_gamma_via_PDE=True --eps=1e-9 --fd_freeze_exe_boundary=True

Via regression method (see the paper Simulated Greeks for American Options):

python optimal_stopping/run/run_algo.py --configs=table_greeks_1,table_greeks_1_2 --nb_jobs=1 --compute_greeks=True --greeks_method="regression" --reg_eps=5 --eps=1e-9 --poly_deg=9 --fd_freeze_exe_boundary=True

For the binomial model:

python optimal_stopping/run/run_algo.py --configs=table_greeks_binomial --nb_jobs=1 --compute_greeks=True --greeks_method="central" --fd_compute_gamma_via_PDE=True --eps=1e-9

Get greeks plot:

python optimal_stopping/run/run_algo.py --configs=table_greeks_plots --nb_jobs=48 --compute_greeks=True --greeks_method="regression" --reg_eps=5 --eps=1e-9 --poly_deg=2 --fd_freeze_exe_boundary=True
python optimal_stopping/utilities/plot_greeks.py

Get tables for sensitivity to randomness of hidden layers:

python optimal_stopping/run/run_algo.py --configs=SensRand_greeks_table1,SensRand_greeks_table1_1 --nb_jobs=1 --path_gen_seed=1 --compute_greeks=True --greeks_method="central" --fd_compute_gamma_via_PDE=True --eps=1e-9

Generate additional tables from paper

To get the table from the paper, run afterwards:

python optimal_stopping/utilities/get_comparison_csv.py

License

This code can be used in accordance with the LICENSE.

Citation

If you use this library for your publications, please cite our paper: Optimal Stopping via Randomized Neural Networks.

@article{OptStopRandNN2021,
author    = {Herrera, Calypso and Krach, Florian and Ruyssen, Pierre and Teichmann, Josef },
title     = {Optimal Stopping via Randomized Neural Networks},
journal   = {Frontiers of Mathematical Finance},
year      = {2023},
url       = {https://www.aimsciences.org/article/doi/10.3934/fmf.2023022}}