C++ testbed for (transcendental) function approximations

Tests function approximations for speed and precision and can plot the results. The currently testable functions are:

floating-point decadic logarithm (base 10)
floating-point square root
floating-point inverse square root
integer square root

Note that these are approximations only with varying degrees of precision and speed and all have their own strengths and weaknesses or may have certain range requirements. I consciously left out tricks like using assembler code or SSE / NEON. These should be obvious and can be used in conjuction with some of the the methods here. Also a good compiler makes some of those optimizations for you anyway. Note that you should compile with optimizations on (-O2 -ffast-math), otherwise your results will be skewed!

Contributions like bug fixes, improvements or new approximation functions are welcome as pull requests.

License

All my own work is under the MIT License, but I am standing on the shoulders of giants:

cxxopts (MIT License)
sciplot (MIT License)
There's no licenses for most of the approximation functions, but I've tried at least attributing them or stating the source in the comments.

Building

Prequisites

Clone repo with all submodules using git clone --recursive https://github.com/HorstBaerbel/approx or update all submodules after cloning using git submodule init && git submodule update.
Use a C++17-capable compiler.
GNUplot 4.2 or higher installed if you want to plot results.

From the command line

Navigate to the approx folder, then:

mkdir build && cd build
cmake ..
make -j$(nproc)

From Visual Studio Code

Must: Install the "C/C++ extension" by Microsoft.
Recommended: If you want intellisense functionality install the "C++ intellisense" extension by austin.
Must: Install the "CMake Tools" extension by Microsoft.
You might need to restart / reload Visual Studio Code if you have installed extensions.
Open the approx using "Open folder...".
Choose a kit of your choice as your active CMake kit if asked, or let CMake decide on its own.
You should be able to build now using F7 and build + run using F5.

Usage

Run approx with the following options:

-h or --help: Show help.
-f FUNC or --function FUNC: Test function, where FUNC can be:
- log10f: Test approximations for the float log10 function.
- invsqrtf: Test approximations for the float 1 / square root function.
- sqrtf: Test approximations for the float square root function.
- sqrti: Test approximations for the 32-bit square root function.
-p FORMAT or --plot FORMAT: Plot results using GNUplot (must be installed) where FORMAT can be:
- pdf: Output result plots to result.pdf file.
- html: Output result table and plots to result.html file.

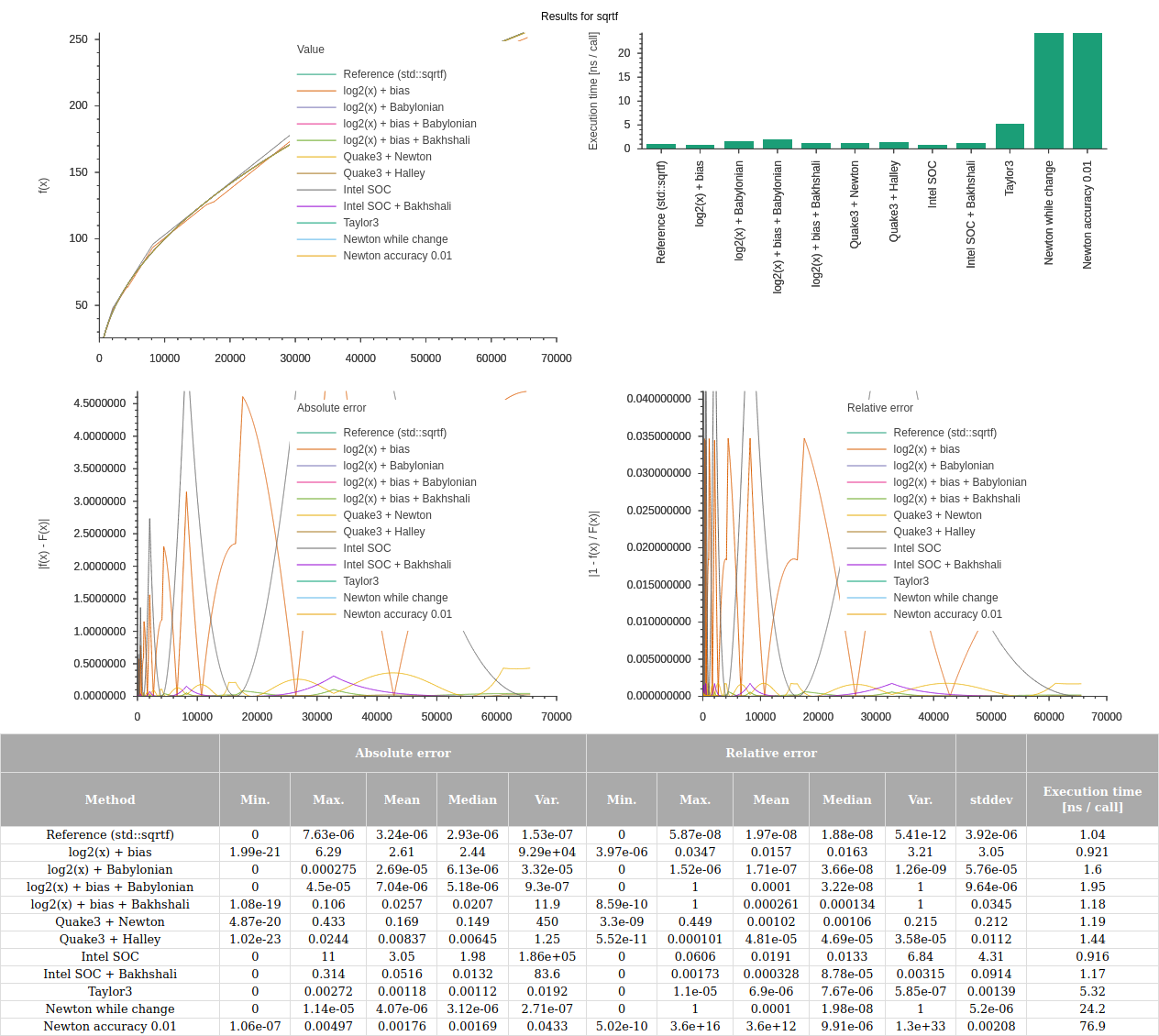
The result is a listing of every function tested, its min/max absolute and relative errors, the standard deviation and the execution time per call, e.g.

Testing: sqrtf
Input range: (1.17549e-38, 65535), 10000 samples in range
Approximate loop and call overhead (already subtracted): 0.2728 ns / call
Tested functions:

#0 - Reference
Absolute error: (0, 7.62852e-06), mean: 3.24438e-06, median: 2.93015e-06, variance: 1.53489e-07
Relative error: (0, 5.87042e-08), mean: 1.96719e-08, median: 1.87608e-08, variance: 5.40974e-12
Standard deviation: 3.9181e-06
Execution time: 1.1701 ns / call

...

#2 - log2(x) + Babylonian
Absolute error: (0, 0.000275493), mean: 2.6902e-05, median: 6.12509e-06, variance: 3.31772e-05
Relative error: (0, 1.52183e-06), mean: 1.7114e-07, median: 3.65627e-08, variance: 1.26044e-09
Standard deviation: 5.76032e-05
Execution time: 1.6986 ns / call

Also a result.html or result.pdf file will be saved to the current directory if you specified "-p":

Todo

Add more functions (1/x, sin / cos / tan / atan2 / etc.).
Improve error and timing statistics plots.

HorstBaerbel/approx