Thoroughly-tested package, called Rubik, that is a representation of the Rubik's Cube in go-lang. A naive and limited BFS solver is provided. It contains functions for all normal moves, slice moves, double moves and cube rotations.
It also contains a package Rubik-alg that can execute algorithms and reverse algorithms. Rubik-alg can also scramble cubes.
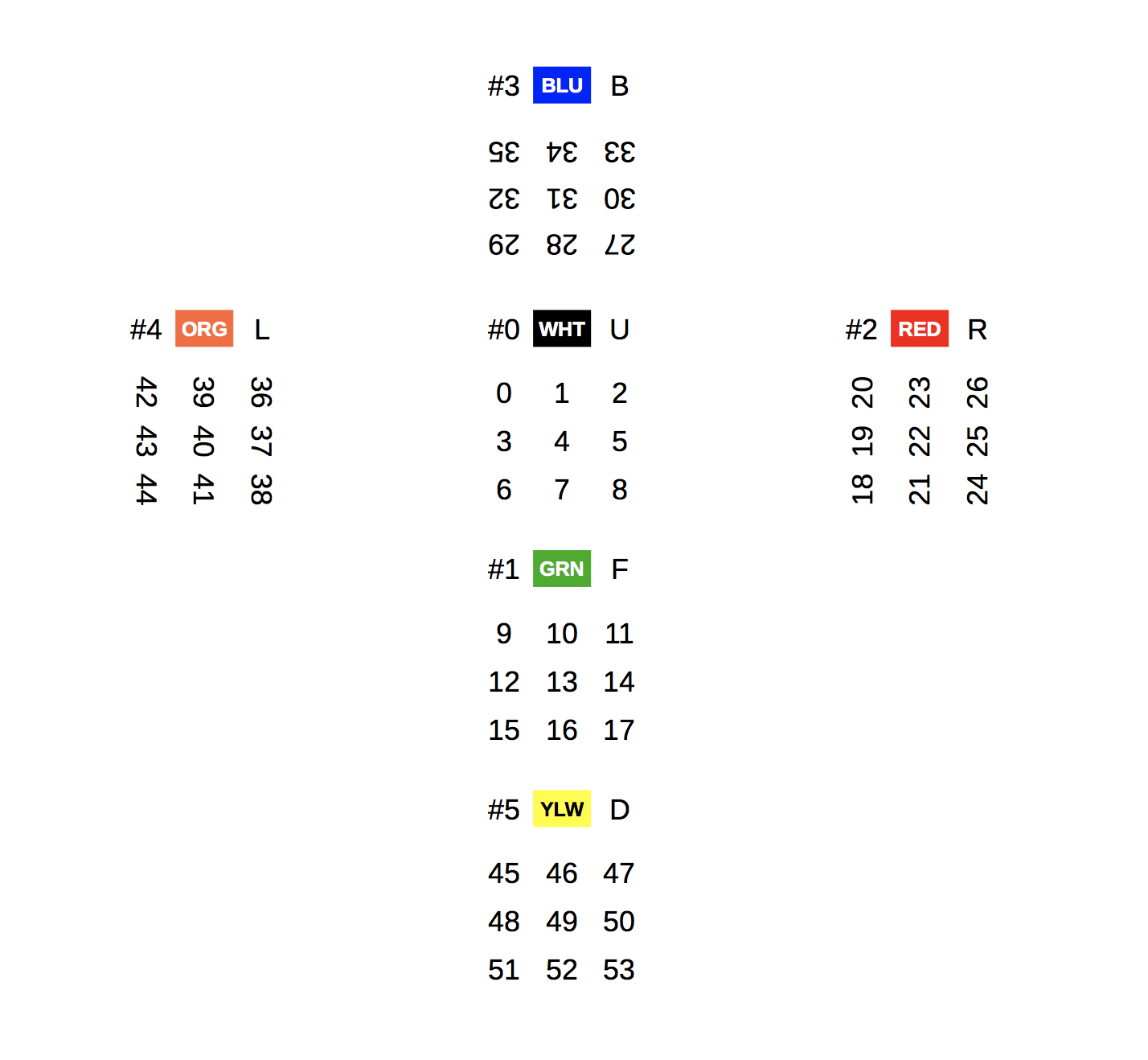
The cube is represented as a []rune:
Cube faces are numbered from #0 (white, upward) to #5 (yellow, downward). By convention, the face color is the color of the square in its center, the one that never moves. You are free to disregard the proposed color, position and numbering scheme in this picture so long that you manipulate valid cubes.
You can instantiate a new solved cube, or with the initial state of your choice.
cube := rubik.NewSolvedCube()
scrambled := rubik.NewCube("bwwbwwyyr orwogbygb gbbrrwrrw ooygbygbr oogoogyyb rrwgywgyo")
Then move the faces. For instance, front face clockwise, upper face clockwise, right face clockwise, and finally upper face counterclockwise:
moved := cube.F().U().R().Uc()
The cube is immutable, so each manipulation returns a new cube.
A naive solver that uses BFS is available. But because the resolution space is very large, the solver will only work on slightly scrambled cubes (3-4 moves away from a solved cube), even though cycles are detected and eliminated.
Beyond that, it will only consume time and fail with insufficient memory.
solved := rubik.Solve(cube)
See better algorithms or Algorithms for solving the Rubik's cube - Harpreet Kaur by Harpreet Kaur.
Contains the cube implementation, and functions for :
- Create a solved cube
- Check if the cube solved
- Check if a cube equals another cube
- Copy a cube
- Normal moves : R, R', L, L', U, U', D, D', F, F', B, B'
- Called R(), Rc()...
- Slice moves : M, M', S, S', E, E'
- Called M(), Mc()...
- Double moves : r, r', l, l', u, u', d, d', f, f', b, b'
- Called Rd(), Rdc()...
- Rotation moves : x, x', y, y', z, z'
- Called X(), Xc()...
It also contains a naive solver.
Contains functions for :
- Execute an algorithm, ex "F' U' x L U' R d2 S'".
- Reversing an algorithms, ex "S d2 R' U L' x' U F".
- Get a scrambled cube, and the scramble algorithm.
Parentheses and brackets in the algorithms are ignored.
Tests are included for all public methods.
Example using the PerformAlg function:
// Perform a T permutation
cube := PerformAlg(cube, "(R U R' U') (R' F R2 U') R' U' (R U R' F')")
fmt.Println(cube) // Prints : "wwwwwwwww ggrgggggg bogrrrrrr rbbbbbbbb orooooooo yyyyyyyyy"You can reverse algorithms using the ReverseAlg function:
alg := ReverseAlg("(R U R' U') (R' F R2 U') R' U' (R U R' F')")
fmt.Println(alg) // Prints "F R U' R' U R U R2 F' R U R U' R'"Get a scrambled cube by using the GetScrambledCube function:
cube, alg := GetScrambledCube()
fmt.Println(cube, alg)