Ce TP poursuit votre apprentissage à l'algorithmie avec le langage de programmation Python.
Celui-ci est composé de 6 exercices, pour lesquels vous devez compléter le code avec l'indicateur TODO.
Tout d'abord, assurez-vous d'avoir téléchargé les fichiers exercices1-6.py que vous devrez compléter. Pour ce TP, vous ne pouvez pas importer d'autres librairies que celle qui sont déjà importées dans les fichiers.
Écrire un programme qui saisit un tableau d’entiers et le trie. Attention, vous ne pouvez pas utiliser de fonction de tri venant d'une librairie, ni la fonction min() et max() et toutes les manipulations doivent se faire sur un seul tableau. Le programme doit ensuite afficher le tableau trié. Pas besoin de modifier le main, effectuez le tri sur le tableau passé en paramètre de la fonction exercice1(tableau).
Votre tri devra suivre la logique suivante présentée dans l'image suivante.
def exercice1(tableau):
#TODO: trier le tableau
return tableau
if __name__ == '__main__':
# Voici un exemple de tableau à trier:
tableau_a_trier = [2,4,6,4,6,7,8,9,7,5,4,3]
resultat = exercice1(tableau_a_trier)
print(resultat)Dans cet exercice, le mot "expression" désigne une chaîne de caractères ne contenant que des parenthèses ouvrantes et fermantes. Par exemple "(()())", "(()()" et "(()))(". Une expression est bien parenthésée si le nombre de parenthèses ouvrantes est égal au nombre de parenthèses fermantes, et si quelque soit la position dans l'expression, le nombre de parenthèses ouvrantes qui précèdent cette position est toujours supérieur ou égal au nombre de parenthèses fermantes qui précèdent.
• "(()())" est une expression bien parenthésée.
• "(()()" est mal parenthésée car il y a 3 parenthèses ouvrantes et 2 parenthèses fermantes seulement.
• "(()))()" est mal parenthésée car le cinquième caractère est la troisième parenthèse fermante, alors qu'il n'y a que deux parenthèses ouvrantes qui précèdent.
Dans cet exercice l'utilisateur va entrer une expression et, si l'expression est mal parenthésée, la fonction retourne "Incorrect", sinon elle retourne la même expresion, mais en insérant des '.' à chaque fois qu'une parenthèse ouvrante est suivie d'une parenthèse fermante. Voici un exemple pour illustrer ce qui est attendu:
est la hauteur avant le rebond numéro
, et
la hauteur après le rebond numéro
.
est la vitesse de la balle avant le rebond numéro
, et
est la vitesse après le rebond
.
Les relations entre les variables sont les suivantes :
=
, avec
la constante de gravité égale à
dans notre cas.
=
avec c le coefficient de rebond.
=
Utilisez une structure de répétition pour calculer le nombre de rebonds necessaire à la balle afin que sa hauteur atteigne 1 cm du sol. Vous ne pouvez pas utiliser de structures de données.
Dans cet exercice, vous devez écrire un programme qui permet de calculer une valeur approchée de par la méthode de Monte‐Carlo basée sur les probabilités.
L’idée est la suivante : si on insère un cercle de rayon 1 (soit un cerle d'aire égale à ) dans un carré de côté 2 (et donc d’aire égale à
), la probabilité qu’un point placé aléatoirement dans le carré soit également dans le cercle est donc de
(le rapport des aires).
Afin d'estimer la valeur de , voici la procédure que vous devez implémenter :
- générer itérativement deux nombres réels aléatoires x et y, tous deux compris entre -1 et 1.
- vérifier l'appartenance du point au cercle : si
+
<
, le point est à l'intérieur du cercle.
- estimer la valeur de
en calculant le ratio entre les points à l'intérieur du cercle et les points à l'intérieur du carré, itérativement, jusqu'à ce que l’écart relatif entre votre estimation et la valeur précise de
Votre fonction doit retourner un tuple qui contiendra votre estimation de et le nombre d'itérations que le programme a effectué pour arriver à ce résultat.
Vous devez utiliser la fonctions random() pour la génération de nombres aléatoires.
Dans cet exercice, vous devez implémenter la multiplication entre deux matrices de tailles quelconque.
Une matrice sera représentée comme une liste de liste. Par exemple, la liste : [[1, 2, 3], [3, 4, 5]] constitue une matrice de deux lignes et trois colonnes où [1, 2, 3] est la premiere ligne.
- Dans un premier temps, vous devez compléter la fonction suivante:
def matriceZero(nbLignes, nbColonnes):
A = []
#TODO: Remplir la matrice A de 0, selon les dimensions données
return A- Dans un second temps, vous devez implémenter la multiplication des matrices. Attention: il faut s'assurer que les deux matrices peuvent être multipliées. Vous pouvez lire sur la multiplication de matrices ici.
def multiplierMatrices(A, B):
#TODO: Si les matrices ne peuvent pas etre multipliées, affecter à C une matrice nulle [nbLignesA x nbColonnesB]
C =
#TODO: Sinon faire la multiplication et mettre dans C le résultat
C =
return CL'affichage attendu à la fin du programme est le suivant:
Dans cet exercice, vous allez participer à la conception d'un système de filtrage des spams RENEGE (useR awarE bayesiaN filtErinG systEm). Ce système permet d’étiqueter les courriels en déduisant si ce sont des spams (non désirés) ou des hams (messages ok). Il s’agit essentiellement d’un classificateur bayésien associé à des règles heuristiques.
Vous ne devrez pas implémenter l'entièreté du système, mais simplement créer un vocabulaire qui sera utilisé pour entrainer les algorithmes d'intelligence artificielle de RENEGE. Dans le fichier email.json, vous avez une liste de 1000 courriels, avec les attributs suivants :
- From: le destinataire du courriel.
- Date: la date du courriel.
- Body: la liste des mots qui sont contenus dans le courriel.
- Spam: si la valeur est 'true', le courriel est un Spam, sinon c'est un Ham.
Le fichier email.json à été sauvegardé dans la variable 'emails' sous forme d'une liste de dictionnaires avec la fonction
with open('email.json') as json_data:
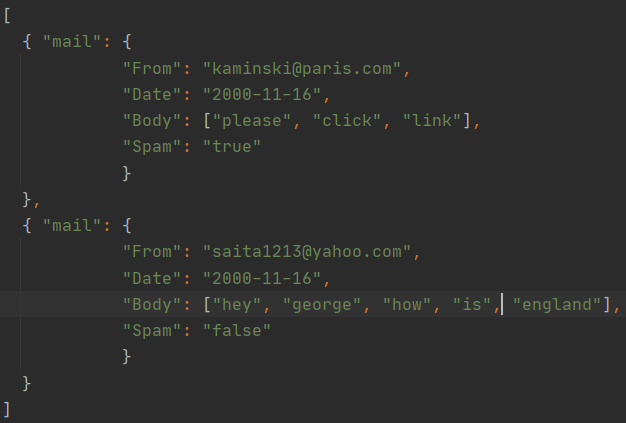
emails = json.load(json_data)Voici à quoi ressemble la structure de la variable emails:
Vous n'avez pas besoin d'arrondir le résultat.
Votre résultat final sera injécté dans fichier results.json, avec la fonction :
with open('results.json', 'w') as fp:
json.dump(result, fp, indent=4)où la variable result contient le dictionnaire en question.
Voici à quoi ressemble la fonction à compléter:
def createVocabulary():
#les mails contient la structure de donnée présente dans mail.json
with open("mails.json") as json_data:
email = json.load(json_data)
#TODO: Affécté à la variable 'result' le résultat final
result = {}
with open('results.json', 'w') as fp:
json.dump(result, fp, indent=4) Vous êtes libre d'implémenter d'autres fonctions pour clarifier le code et éviter les répétitions. Nous vous recommendons de réfléchir aux structures de données les plus adaptées pour résoudre ce problème efficacement. En effet la fonction createVocabulary() doit s'exécuter dans un temps acceptable.