Ad auction bidding strategy

Theory

Consider the case of participating in N ≫ 1 online ad auctions with a limited bidding budget. The task is to create such a bidding strategy that you can win some of them, and that the placed ads generate at least $n_{click}$ clicks. This should be done by spending as little money as possible.

The ad auctions can be put into several groups based on:

the probability $p_{ctr}$ that a user will click on the displayed ad if we win the auction
the probability $p_{aucwin}$ to win an auction if we place a bid

The optimal bids for the different auction groups are obtained by the constrained optimization problem where we have to minimize the expected spent budget $f(x)$ given that the difference between expected number of generated ad-clicks and $n_{click}$, $g(x)$, is zero:

$$ \begin{align*} f(x) & = \sum_{m\in\mathcal{M}} n_m \cdot x_m \cdot p_{aucwin,m}(x_m), \\ g(x) & = \sum_{m\in\mathcal{M}} n_m \cdot p_{ctr,m} \cdot p_{aucwin,m}(x_m) - n_{click} \end{align*} $$

where $\mathcal{M}$ refers to the different auction groups and $n_m$ to the number of auctions that belong to this group.

We assume that the number of auction groups $\mathcal{M}$, group sizes $\lbrace n_m\vert m\in\mathcal{M}\rbrace$ and ctr probabilities $\lbrace p_{ctr,m} \vert m\in\mathcal{M} \rbrace$ can be easily inferred from past events. To obtain the probability of winning an auction we have implemented two options:

Construct it directly from the winning-bids $\lbrace s_i\vert i\in\mathcal{I} \rbrace$ from past auctions of this type ($\Theta(x) = 1$ if $x>0$ and $0$ otherwise):

$$ \begin{align*} p_{aucwin} (x) & = \sum_{i\in \mathcal{I}} \Theta(b_i < x) \Big/ \sum_{i\in \mathcal{I}} 1, \end{align*} $$

Use the cumulative distribution function of an analytical function for the distribution of winning bids $p_{winbid}$ obtained, for example, through some variational inference approach:

$$ \begin{align*} p_{aucwin}(x) & = \int^{x}_{0} p_w (b) \cdot db \end{align*} $$

A detailed description of the problem and the possible solutions is provided in this document.

Implementation

The optimization problem is solved numerically 10 times and the best solution is used as a final result.

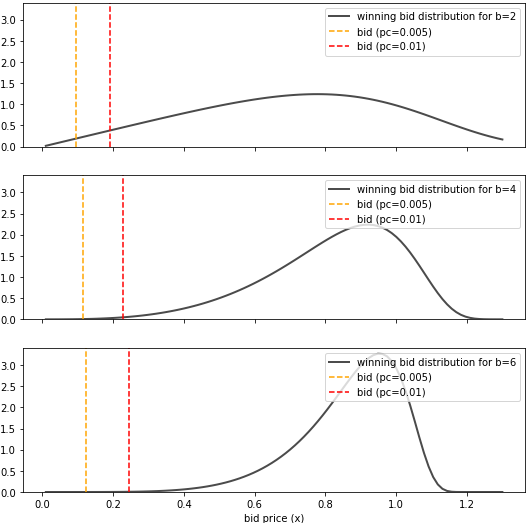
An example how to find the bid strategy for two auction groups with if we use analytical functions for the winning bid distributions is provided below:
```
PYTHONPATH=src python src/main.py optimize \
    --n-click=100 \
    --p-ctr='0.02, 0.02' \
    --n='20_000, 10_000' \
    --winbid-dist='[{"name": "exponpow", "params": {"b": 2}}, {"name": "exponpow", "params": {"b": 4}}]' \
    --winbid-dist-analytical
```
We have used the exponential power distribution to describe the winning bid distributions of both auction groups.

To solve the same problem by using samples of the winning-bids from past auctions, we first have to generate these samples:

PYTHONPATH=src python src/main.py generate-data \
    --winbid-dist='[{"name": "exponpow", "params": {"b": 2}},{"name": "exponpow", "params": {"b": 4}}]' \
    --save-path='data.json'

The use these samples in the algorithm set winbid-dist to the path where the samples are stored ('data.json') and remove the --winbid-dist-analytical flag:

PYTHONPATH=src python src/main.py optimize \
    --n-click=100 \
    --p-ctr='0.02, 0.02' \
    --n='20_000, 10_000' \
    --winbid-dist='data.json'

More examples are provided in this Jupyter notebook and can be tested in this google colab notebook

Original solution

The code used for the solution of the problem described in this blog post can be found in this release

ImScientist/auction-bidding-strategy

Ad auction bidding strategy

Theory

Implementation

Original solution