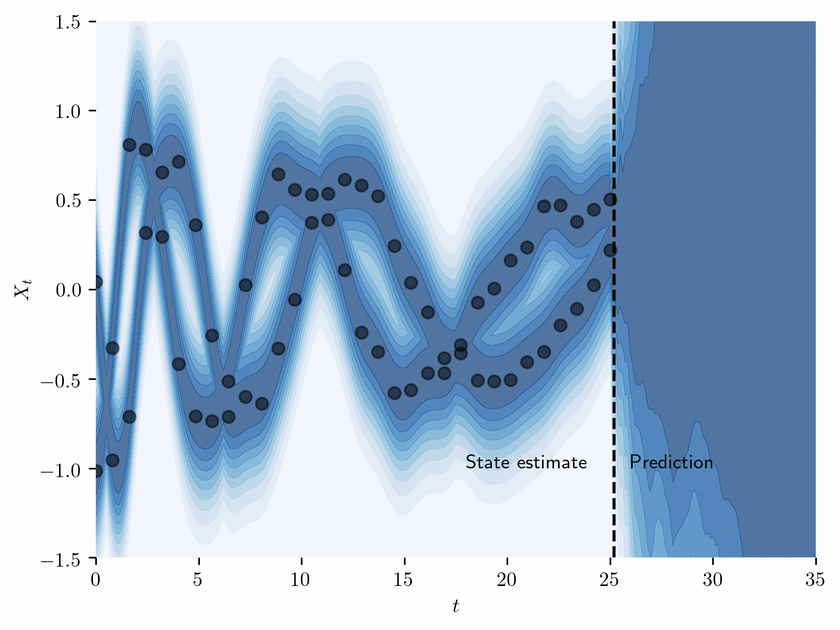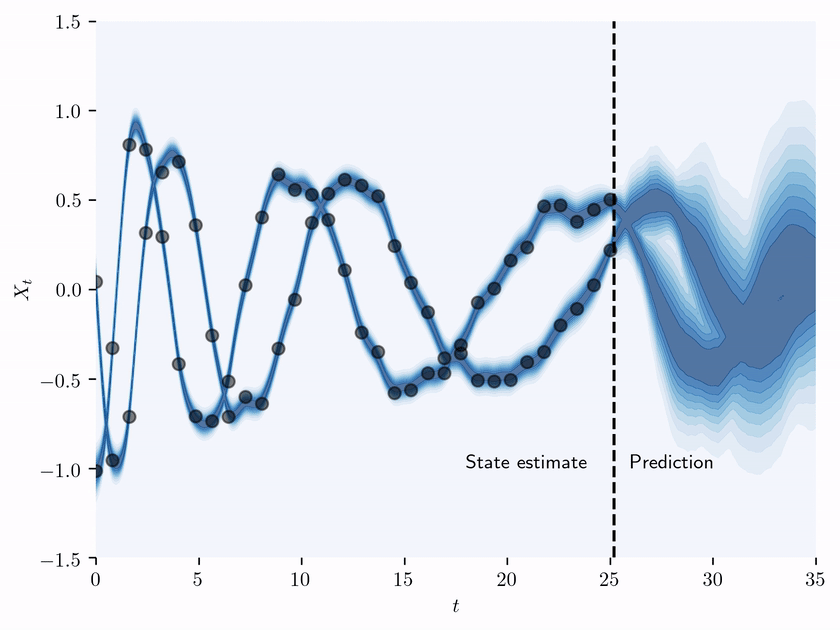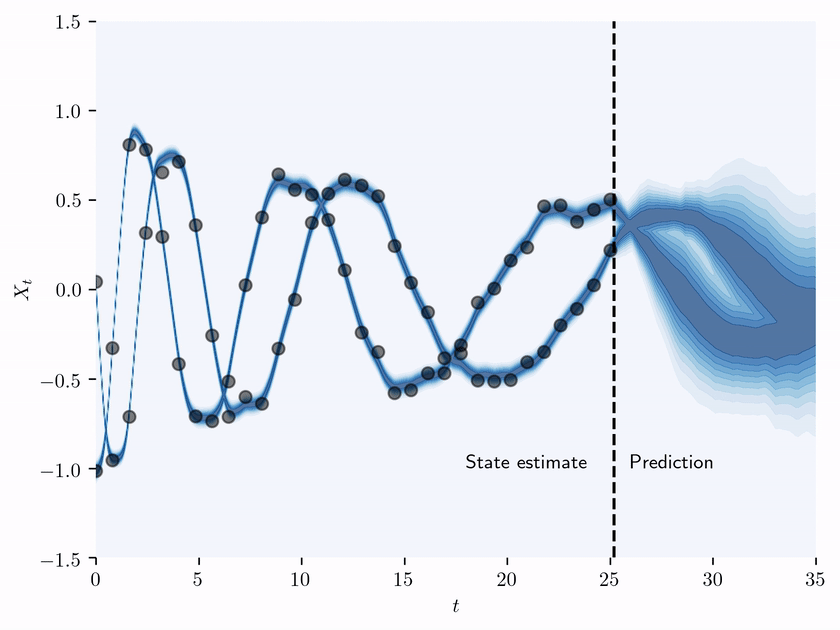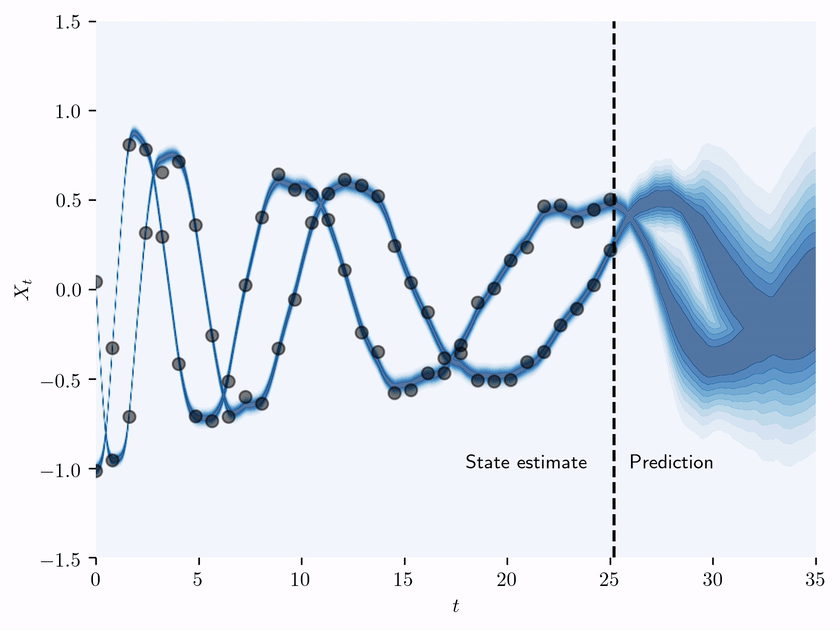
Accompanying code for "State estimation of a physical system with unknown governing equations" by Kevin Course and Prasanth B. Nair.
Tutorials and docs coming soon!
If you just want to use the package,
you can install svise from PyPI.
If you wish to reproduce experiments / figures, we recommend installing optional dependencies.
pip install sviseThe best place to learn about the package is the documentation.
We use conda-lock and poetry to manage dependencies (although we wouldn't recommend it...).
After installing conda-lock, follow the steps below to install all dependencies used in the experiment environment.
- Clone the repository.
git clone https://github.com/coursekevin/svise.git- Navigate into the directory and create a new conda environment.
conda-lock install --name svi-state-estimation conda-lock.yml- Activate the environment that was just created.
conda activate svi-state-estimation- Install the remaining dependencies.
poetry install --with dev- Run tests to confirm everything was install correctly. (Some tests are stochastic so might fail on some attempts. If any tests fail, run again before filing an issue.)
pytest tests/Dependencies:
- see
pyproject.tomlfor a complete list of dependencies.
- Download pretrained models, data, and figures:
repopacker download svise-pack.zip
repopacker unpack svise-pack.zipThis will download everything except for the cylinder data used in the third example. The cylinder data is split up in seven 3.2GB chunks. Download all the chunks and combine the data with:
cat cylinder_data_split.z*[0..9]* cylinder_data_split.zip > cylinder_data.zipUnzip the data move the file vortex.pkl into the directory
/experiments/3_cylinder_flow/dataThe numerical studies can be rerun from the experiments directory using
the command-line script main.py. All numerical studies follow the
same basic structure: (i) generate datasets, (ii) train models / run
methods, and (iii) post process for figures and tables.
- Generate dataset for a specific experiment. The newly generated dataset can be found in the experiment subdirectory.
python main.py [experiment] generate-data-
Experiments in main text:
pure-se(state estimation without corruptions)corrupted-se(state estimation without probabilistic corruptions)cylinder-flow(Cylinder-flow reduced-order modeling experiment)
-
Examples in Methods:
symb-goveq-disc(discovering governing equation experiments)second-order-disc(second order governing equation discovery)ext-goveq-disc(Lorenz '96 experiment)binary-black-hole(Binary black hole problem)
- Train a model on a dataset optionally specifying the random seed. The model will be saved in the experiment subdirectory. If there is only one dataset (such as is true for the cylinder-flow problem) there is no need to specify the dataset path.
python main.py [experiment] run-[method] -dp path/to/dataset.pt -rs seed- Methods:
svise(stochastic variational inference for state estimation)pf(particle filter)sindy(SINDy with STLSQ + SINDy with SR3)
- Post process results for figures and tables. Any figures or tables can be found in the experiment subdirectory. This script expects there to be one model / dataset. Undefined behavior may occur if this is not the case.
python main.py [experiment] post-processBuilding documentation requires Sphinx
and the Read the Docs Sphinx Theme.
First navigate into the docs directory.
Building html docs:
make htmlBuilding pdf docs:
make latexpdfCompleted docs can be found in the docs/_build directory.
Course, K., Nair, P.B. State estimation of a physical system with unknown governing equations. Nature 622, 261–267 (2023). https://doi.org/10.1038/s41586-023-06574-8