Ling xie
ENM 502-001
2021-03-08
Assignment 3 Newton method and Arc-length continuation
Introduction
In this assignment, we would solve a non-linear boundary-value problem defined on the unit-square domain $$ \begin{aligned} &\begin{array}{l} D=(0 \leq x \leq 1) \cup(0 \leq y \leq 1) \ \nabla^{2} u+\lambda u(1+u)=0 \end{array}\ &u(x, y)=0 \text { on all boundaries, } \end{aligned} $$
with newton method. After we guess the initial solution on some typical lambda, we track track and iterate lambda from
$$
0 \leq \lambda \leq 60
$$
with analytic continuation(AyC) and arc-length continuation(ARCLC).
Problem Setup and Formulation
Discretization and centered finite difference applied to this problem.
We discretize the U with finite difference method, in specifically a 30 X 30 uniform grid.
Newton's Method
As a fixed-point iteration method, given a initial approximation at U_0, newton's method would approximate the solution in the derivative direction.
The iteration goes like $$ \mathbf{u}^{k+1}=\mathbf{u}^{k}+\delta \mathbf{u}^{k} $$ where $ \delta \mathbf{u}^{k} $ is calculated by $$ \left.{\mathbf{J}}\right|{k}\left(\begin{array}{1} {\partial \mathbf{u}} \end{array}\right){k}=-\left({\partial {\mathbf{R}}}\right)_{k} $$
where J is the Jacobin matrix.
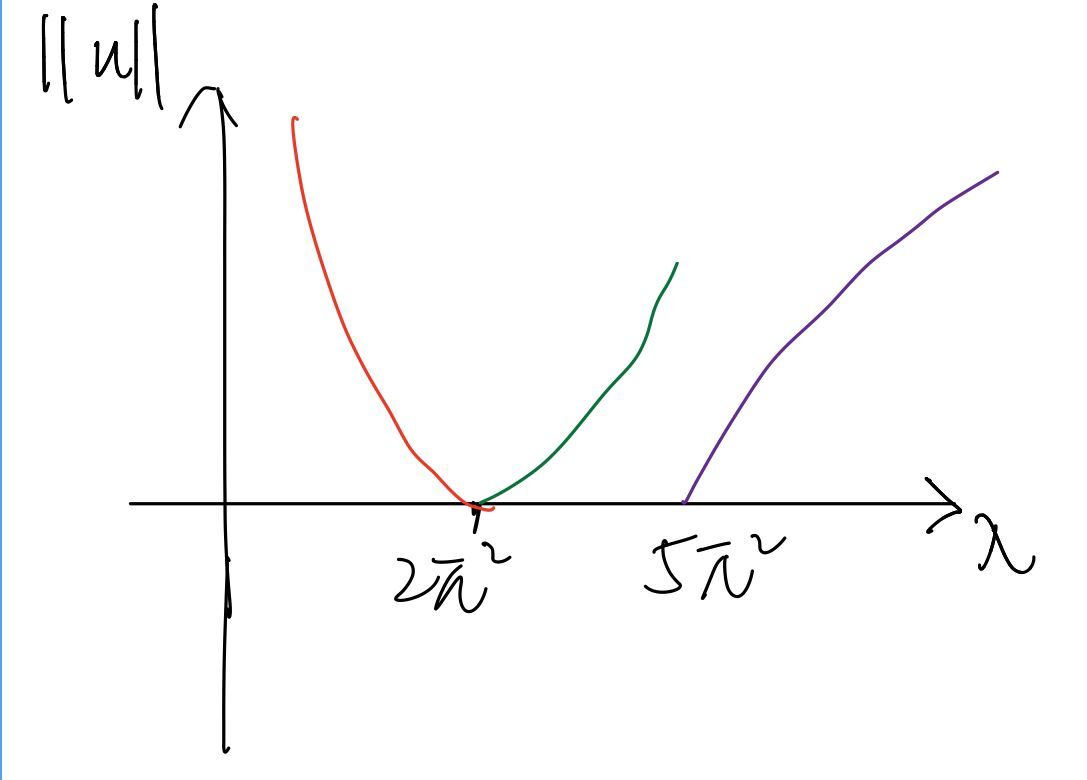
For the initial value, when L2norm of
| lambda = 2 * pi^2 | lambda = 5 * pi^2 | lambda = 5 * pi^2 |
|---|---|---|
 |
 |
 |
Methods to generate first two non-trivial solutions (analytical continuation)
We would use newton's method to solve for U_0 from first initial guess(see image above). To calculate U_1 , we use AyC to calculate the initial guess U_1_guess, then use newton's method to solve the solution at lambda_1.
Arc-Length Continuation
During iterating the lambda, the J would become nearly singular during turning point. To prevent this, we introduce a new independent variable s.
$$
(\delta S)^{2}=(\delta \lambda)^{2}+|\delta \mathbf{u}|_{2}^{2}
$$
and start to iterate on s for the rest steps.
For each iteration, let's say we have U_cur, lmbd_cur, U_prv lmbd_prv, which is the solution of k - 1, k - 2iteration(it’s kth iteration)
during every iteration, we first use arc-length initialization to get initial guess , let’s say it be U_cur_init, lmbd_cur_init.
$$
\begin{array}{l}
\mathbf{u}{2}^{0}=\mathbf{u}{1}+(\delta s)\left(\frac{\partial \mathbf{u}}{\partial s}\right){1} \
\lambda{2}^{0}=\lambda_{1}+(\delta s)\left(\frac{\partial \lambda}{\partial s}\right)_{1}
\end{array}
$$
And during arc-length initialization **, we would use U_cur, lmbd_curto create the Jacobin matrix.
The we would use U_cur_init, lmbd_cur_init together with U_prv lmbd_prv to do the full newton iteration. The detailed iteration could be viewed as below.
$$
\begin{array}{l}
\left.\left.\left(\hat{\mathbf{J}}^{k}\right)\right|{s 2}\left(\begin{array}{c}
\delta \mathbf{u}^{k} \
\delta \lambda^{k}
\end{array}\right)\right|{s 2}=-\left.\left(\hat{\mathbf{R}}^{k}\right)\right|_{s 2} \
\lambda^{k+1}=\lambda^{k}+\delta \lambda^{k} \
\mathbf{u}^{k+1}=\mathbf{u}^{k}+\delta \mathbf{u}^{k}
\end{array}
$$
Results and Discussion
From my circumstances, I notice that with different mixture of parameters( ARCLC step size, initial point, etc), the results vary rapidly.
Failed cases
Rush to bottom
|
|
L2norm of U |
U | U |
|---|---|---|---|
 |
 |
 |
 |
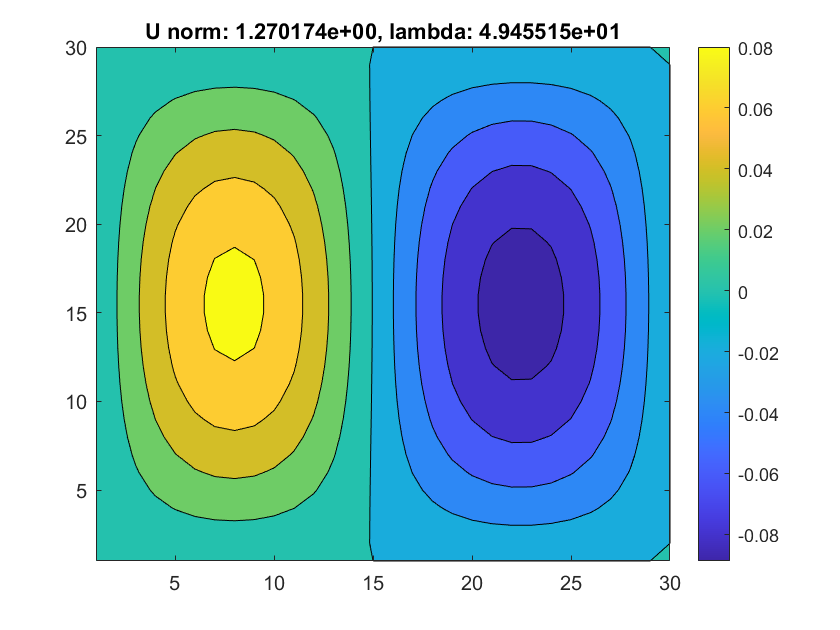
Rush to top
|
|
L2norm of U |
U | U |
|---|---|---|---|
 |
 |
 |
 |
Rush to top
|
|
L2norm of U |
U | U |
|---|---|---|---|
 |
 |
 |
 |
Up and down
|
|
L2norm of U |
U | U |
|---|---|---|---|
 |
 |
 |
 |
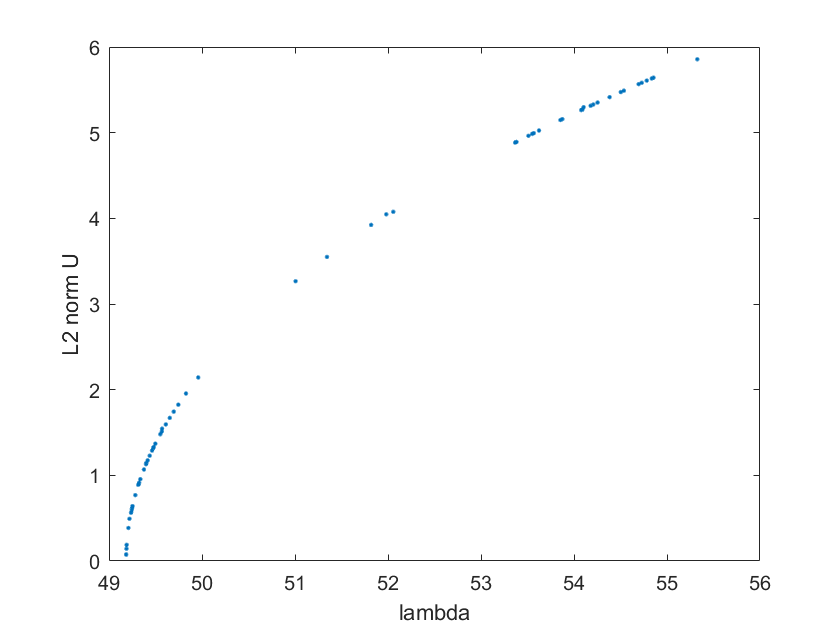
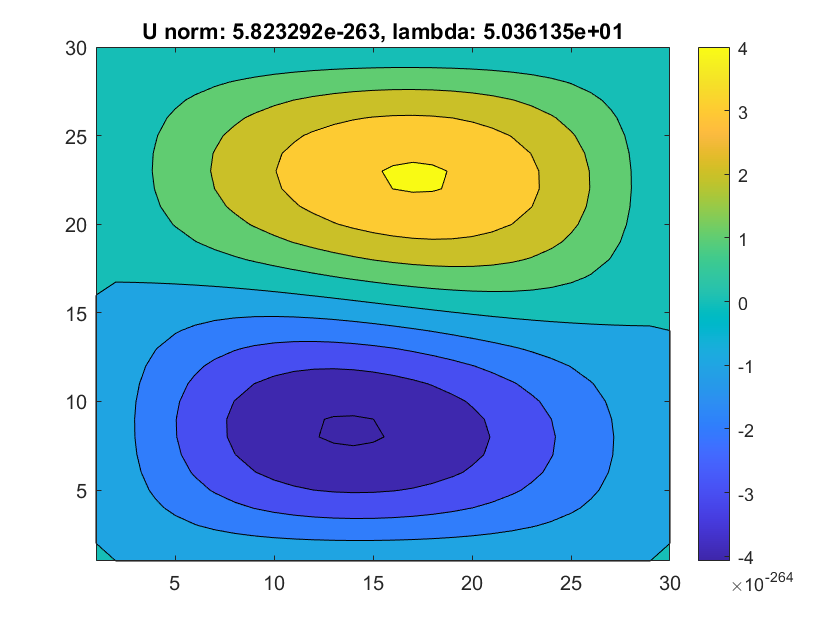
Relatively make sense cases
|
|
L2norm of U |
U | U |
|---|---|---|---|
 |
 |
 |
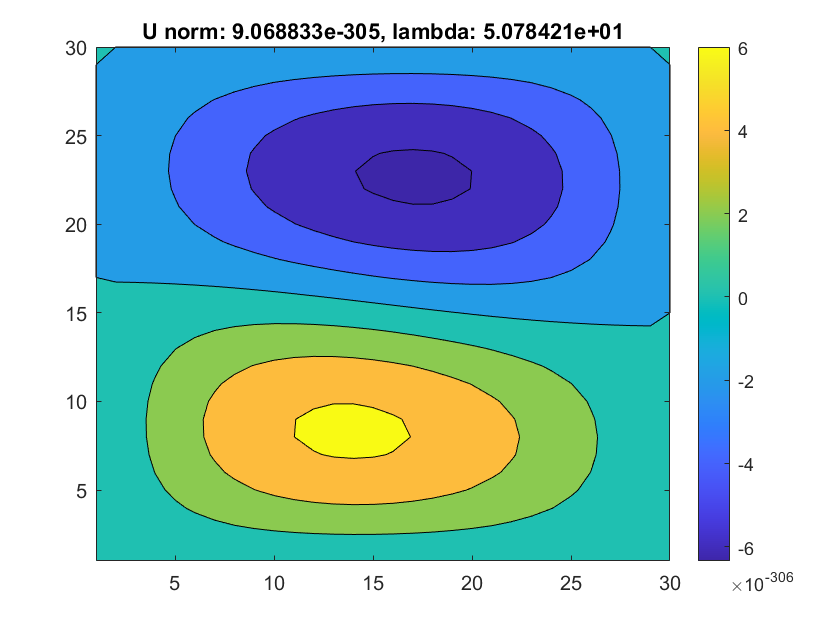 |
|
|
L2norm of U |
U | U |
|---|---|---|---|
 |
 |
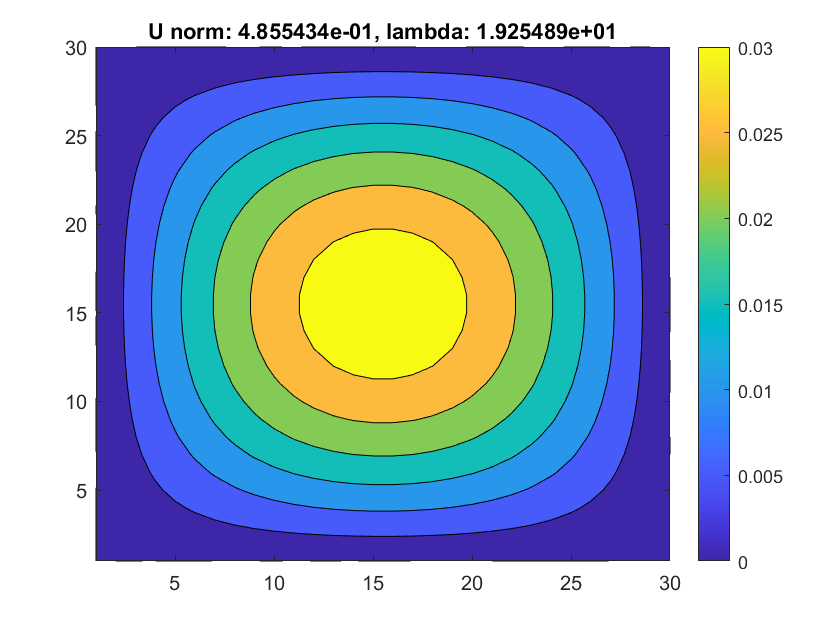 |
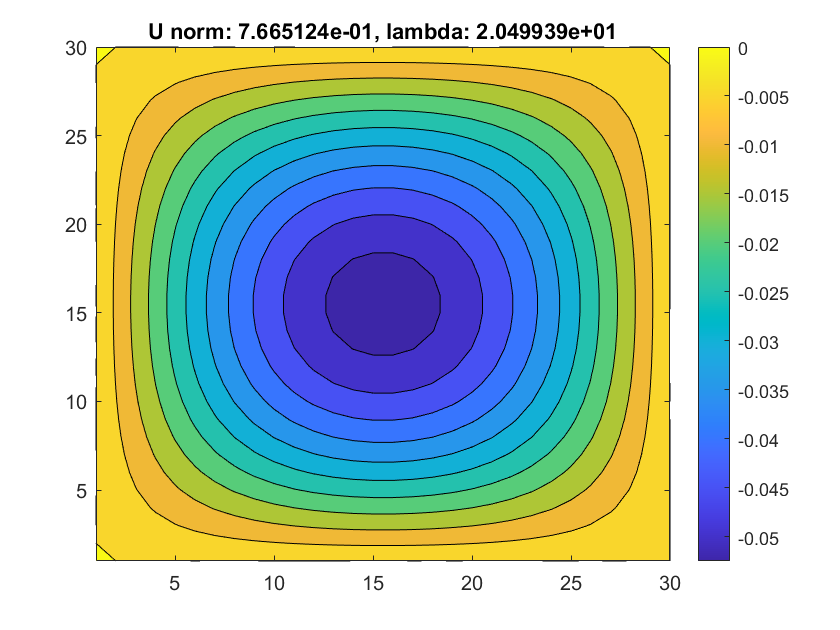 |
Performance with sparse matrix
Here we test the running time during solving the $$ \left.{\mathbf{J}}\right|{k}\left(\begin{array}{1} {\partial \mathbf{u}} \end{array}\right){k}=-\left({\partial {\mathbf{R}}}\right)_{k} $$
| Sparse | Full | |
|---|---|---|
| time(seconds) spent in 64 iterations | 2.158603 | 2.75824 |
Here J is a banded matrix with bandwidth 2n (the whole matrix J is (n+1)^2. As expected, matrix solving under this setting could benefit greatly from sparse matrix.
Conclusion
This is the expected whole graph of L2 norm of U vs iteration.
In my current version or ARCLC, the full newton's method(with J_hat) could hardly converge. I think that's the reason why the lambda vs iteration is not stable and smooth.
Despite, we still manage to see that the U could jump on another branch. As in last two examples, the hill-like and bowl-like solutions change signs when we are moving along the curve.
|
|
L2norm of U |
U | U |
|---|---|---|---|
 |
 |
 |
 |
For this example(see image above), we see that although the it could switch on another branch, the branch could sometimes jump on trivial solution(where the L2norm becomes 0), We guess this is due to the preset d_s is a kind of large step in this settings.
In some rare circumstances(the first results), the U could sometimes move from 5pi^2to 2pi^2 branch.
Code
Code repository is here.