Adaptfilt is an adaptive filtering module for Python. It includes simple, procedural implementations of the following filtering algorithms:
- Least-mean-squares (LMS) - including traditional and leaky filtering
- Normalized least-mean-squares (NLMS) - including traditional and leaky filtering with recursively updated input energy
- Affine projection (AP) - including traditional and leaky filtering
The algorithms are implemented using Numpy for computational efficiency. Further optimization have also been done, but this is very limited and only on the most computationally intensive parts of the source code. Future implementation of the following algorithms is currently planned:
- Recursive least squares (RLS)
- Steepest descent (SD)
To install from PyPI using pip simply run:
sudo pip install adaptfilt
Alternatively, the module can also be downloaded at https://pypi.python.org/pypi/adaptfilt or https://github.com/Wramberg/adaptfilt. The latter is also used for issue tracking. Note that adaptfilt requires Numpy to be installed (tested using version 1.9.0).
Once installed, the module should be available for import by calling:
import adaptfilt
Following the reference sections, examples are provided to show the modules functionality.
In this section, the functions provided by adaptfilt are described. The descriptions correspond with excerpts from the function docstrings and are only included here for your convenience.
y, e, w = lms(u, d, M, step, leak=0., initCoeffs=None, N=None, returnCoeffs=False)
Perform least-mean-squares (LMS) adaptive filtering on u to minimize error given by e=d-y, where y is the output of the adaptive filter.
- Parameters
- u : array-like
- One-dimensional filter input.
- d : array-like
- One-dimensional desired signal, i.e., the output of the unknown FIR system which the adaptive filter should identify. Must have length >= len(u), or N+M-1 if number of iterations are limited (via the N parameter).
- M : int
- Desired number of filter taps (desired filter order + 1), must be non-negative.
- step : float
- Step size of the algorithm, must be non-negative.
- Optional Parameters
- leak : float
- Leakage factor, must be equal to or greater than zero and smaller than one. When greater than zero a leaky LMS filter is used. Defaults to 0, i.e., no leakage.
- initCoeffs : array-like
- Initial filter coefficients to use. Should match desired number of filter taps, defaults to zeros.
- N : int
- Number of iterations, must be less than or equal to len(u)-M+1 (default).
- returnCoeffs : boolean
- If true, will return all filter coefficients for every iteration in an N x M matrix. Does not include the initial coefficients. If false, only the latest coefficients in a vector of length M is returned. Defaults to false.
- Returns
- y : numpy.array
- Output values of LMS filter, array of length N.
- e : numpy.array
- Error signal, i.e, d-y. Array of length N.
- w : numpy.array
- Final filter coefficients in array of length M if returnCoeffs is False. NxM array containing all filter coefficients for all iterations otherwise.
- Raises
- TypeError
- If number of filter taps M is not type integer, number of iterations N is not type integer, or leakage leak is not type float/int.
- ValueError
- If number of iterations N is greater than len(u)-M, number of filter taps M is negative, or if step-size or leakage is outside specified range.
y, e, w = nlmsru(u, d, M, step, eps=0.001, leak=0, initCoeffs=None, N=None, returnCoeffs=False)
Same as nlms but updates input energy recursively for faster computation. Note that this can cause instability due to rounding errors.
y, e, w = nlms(u, d, M, step, eps=0.001, leak=0, initCoeffs=None, N=None, returnCoeffs=False)
Perform normalized least-mean-squares (NLMS) adaptive filtering on u to minimize error given by e=d-y, where y is the output of the adaptive filter.
- Parameters
- u : array-like
- One-dimensional filter input.
- d : array-like
- One-dimensional desired signal, i.e., the output of the unknown FIR system which the adaptive filter should identify. Must have length >= len(u), or N+M-1 if number of iterations are limited (via the N parameter).
- M : int
- Desired number of filter taps (desired filter order + 1), must be non-negative.
- step : float
- Step size of the algorithm, must be non-negative.
- Optional Parameters
- eps : float
- Regularization factor to avoid numerical issues when power of input is close to zero. Defaults to 0.001. Must be non-negative.
- leak : float
- Leakage factor, must be equal to or greater than zero and smaller than one. When greater than zero a leaky LMS filter is used. Defaults to 0, i.e., no leakage.
- initCoeffs : array-like
- Initial filter coefficients to use. Should match desired number of filter taps, defaults to zeros.
- N : int
- Number of iterations to run. Must be less than or equal to len(u)-M+1. Defaults to len(u)-M+1.
- returnCoeffs : boolean
- If true, will return all filter coefficients for every iteration in an N x M matrix. Does not include the initial coefficients. If false, only the latest coefficients in a vector of length M is returned. Defaults to false.
- Returns
- y : numpy.array
- Output values of LMS filter, array of length N.
- e : numpy.array
- Error signal, i.e, d-y. Array of length N.
- w : numpy.array
- Final filter coefficients in array of length M if returnCoeffs is False. NxM array containing all filter coefficients for all iterations otherwise.
- Raises
- TypeError
- If number of filter taps M is not type integer, number of iterations N is not type integer, or leakage leak is not type float/int.
- ValueError
- If number of iterations N is greater than len(u)-M, number of filter taps M is negative, or if step-size or leakage is outside specified range.
y, e, w = ap(u, d, M, step, K, eps=0.001, leak=0, initCoeffs=None, N=None, returnCoeffs=False)
Perform affine projection (AP) adaptive filtering on u to minimize error given by e=d-y, where y is the output of the adaptive filter.
- Parameters
- u : array-like
- One-dimensional filter input.
- d : array-like
- One-dimensional desired signal, i.e., the output of the unknown FIR system which the adaptive filter should identify. Must have length >= len(u), or N+M-1 if number of iterations are limited (via the N parameter).
- M : int
- Desired number of filter taps (desired filter order + 1), must be non-negative.
- step : float
- Step size of the algorithm, must be non-negative.
- K : int
- Projection order, must be integer larger than zero.
- Optional Parameters
- eps : float
- Regularization factor to avoid numerical issues when power of input is close to zero. Defaults to 0.001. Must be non-negative.
- leak : float
- Leakage factor, must be equal to or greater than zero and smaller than one. When greater than zero a leaky LMS filter is used. Defaults to 0, i.e., no leakage.
- initCoeffs : array-like
- Initial filter coefficients to use. Should match desired number of filter taps, defaults to zeros.
- N : int
- Number of iterations to run. Must be less than or equal to len(u)-M+1. Defaults to len(u)-M+1.
- returnCoeffs : boolean
- If true, will return all filter coefficients for every iteration in an N x M matrix. Does not include the initial coefficients. If false, only the latest coefficients in a vector of length M is returned. Defaults to false.
- Returns
- y : numpy.array
- Output values of LMS filter, array of length N.
- e : numpy.array
- Error signal, i.e, d-y. Array of length N.
- w : numpy.array
- Final filter coefficients in array of length M if returnCoeffs is False. NxM array containing all filter coefficients for all iterations otherwise.
- Raises
- TypeError
- If number of filter taps M is not type integer, number of iterations N is not type integer, or leakage leak is not type float/int.
- ValueError
- If number of iterations N is greater than len(u)-M, number of filter taps M is negative, or if step-size or leakage is outside specified range.
mswe = mswe(w, v)
Calculate mean squared weight error between estimated and true filter coefficients, in respect to iterations.
- Parameters
- v : array-like
- True coefficients used to generate desired signal, must be a one-dimensional array.
- w : array-like
- Estimated coefficients from adaptive filtering algorithm. Must be an N x M matrix where N is the number of iterations, and M is the number of filter coefficients.
- Returns
- mswe : numpy.array
- One-dimensional array containing the mean-squared weight error for every iteration.
- Raises
- TypeError
- If inputs have wrong dimensions
- Note
- To use this function with the adaptive filter functions set the optional parameter returnCoeffs to True. This will return a coefficient matrix w corresponding with the input-parameter w.
The following examples illustrate the use of the adaptfilt module. Note that the matplotlib.pyplot module is required to run them.
"""
Acoustic echo cancellation in white background noise with NLMS.
Consider a scenario where two individuals, John and Emily, are talking over the
Internet. John is using his loudspeakers, which means Emily can hear herself
through John's microphone. The speech signal that Emily hears, is a distorted
version of her own. This is caused by the acoustic path from John's
loudspeakers to his microphone. This path includes attenuated echoes, etc.
Now for the problem!
Emily wishes to cancel the echo she hears from John's microphone. Emily only
knows the speech signal she sends to him, call that u(n), and the speech signal
she receives from him, call that d(n). To successfully remove her own echo
from d(n), she must approximate the acoustic path from John's loudspeakers to
his microphone. This path can be approximated by a FIR filter, which means an
adaptive NLMS FIR filter can be used to identify it. The model which Emily uses
to design this filter looks like this:
u(n) ------->->------+----------->->-----------
| |
+-----------------+ +------------------+
+->-| Adaptive filter | | John's Room |
| +-----------------+ +------------------+
| | -y(n) |
| | d(n) |
e(n) ---+---<-<------+-----------<-<----------+----<-<---- v(n)
As seen, the signal that is sent to John is also used as input to the adaptive
NLMS filter. The output of the filter, y(n), is subtracted from the signal
received from John, which results in an error signal e(n) = d(n)-y(n). By
feeding the error signal back to the adaptive filter, it can minimize the error
by approximating the impulse response (that is the FIR filter coefficients) of
John's room. Note that so far John's speech signal v(n) has not been taken into
account. If John speaks, the error should equal his speech, that is, e(n)
should equal v(n). For this simple example, however, we assume John is quiet
and v(n) is equal to white Gaussian background noise with zero-mean.
In the following example we keep the impulse response of John's room constant.
This is not required, however, since the advantage of adaptive filters, is that
they can be used to track changes in the impulse response.
"""
import numpy as np
import matplotlib.pyplot as plt
import adaptfilt as adf
# Get u(n) - this is available on github or pypi in the examples folder
u = np.load('speech.npy')
# Generate received signal d(n) using randomly chosen coefficients
coeffs = np.concatenate(([0.8], np.zeros(8), [-0.7], np.zeros(9),
[0.5], np.zeros(11), [-0.3], np.zeros(3),
[0.1], np.zeros(20), [-0.05]))
d = np.convolve(u, coeffs)
# Add background noise
v = np.random.randn(len(d)) * np.sqrt(5000)
d += v
# Apply adaptive filter
M = 100 # Number of filter taps in adaptive filter
step = 0.1 # Step size
y, e, w = adf.nlms(u, d, M, step, returnCoeffs=True)
# Calculate mean square weight error
mswe = adf.mswe(w, coeffs)
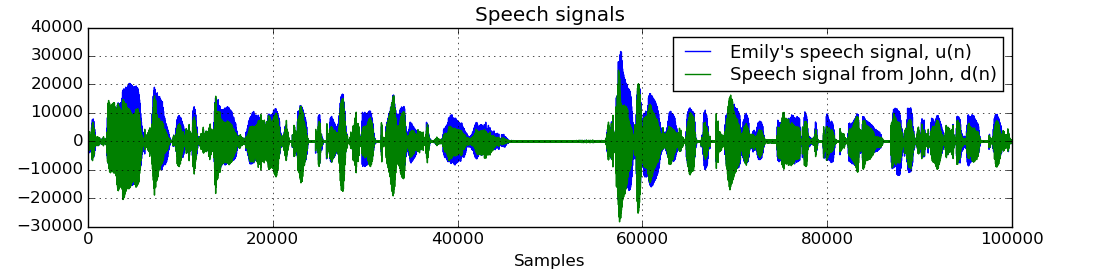
# Plot speech signals
plt.figure()
plt.title("Speech signals")
plt.plot(u, label="Emily's speech signal, u(n)")
plt.plot(d, label="Speech signal from John, d(n)")
plt.grid()
plt.legend()
plt.xlabel('Samples')
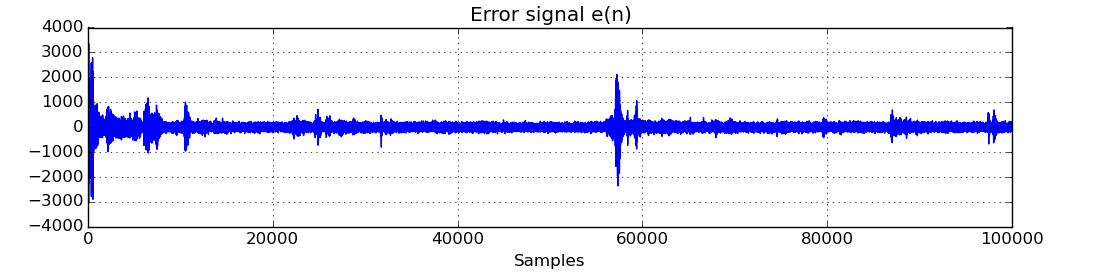
# Plot error signal - note how the measurement noise affects the error
plt.figure()
plt.title('Error signal e(n)')
plt.plot(e)
plt.grid()
plt.xlabel('Samples')
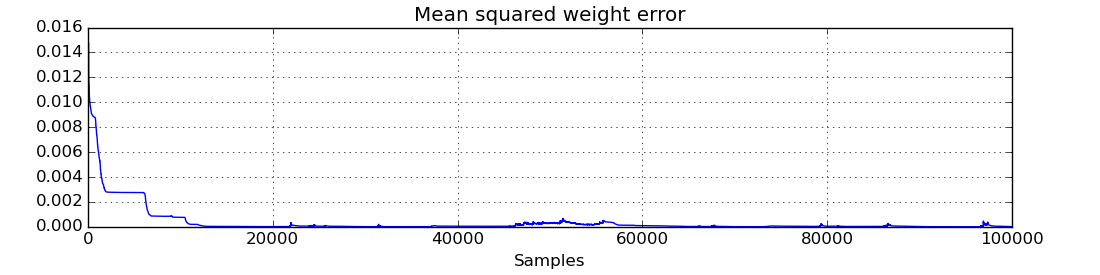
# Plot mean squared weight error - note that the measurement noise causes the
# error the increase at some points when Emily isn't speaking
plt.figure()
plt.title('Mean squared weight error')
plt.plot(mswe)
plt.grid()
plt.xlabel('Samples')
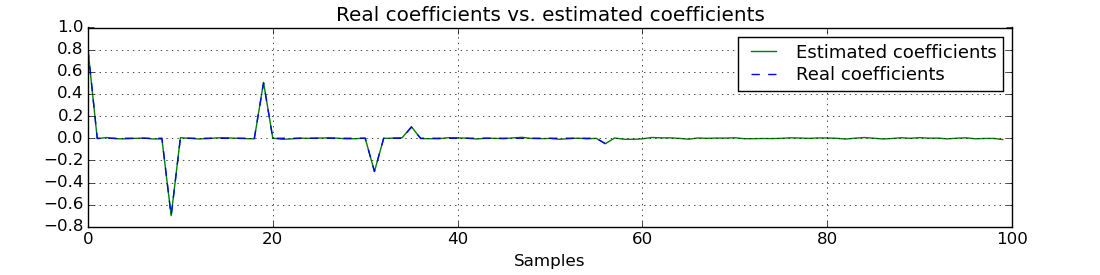
# Plot final coefficients versus real coefficients
plt.figure()
plt.title('Real coefficients vs. estimated coefficients')
plt.plot(w[-1], 'g', label='Estimated coefficients')
plt.plot(coeffs, 'b--', label='Real coefficients')
plt.grid()
plt.legend()
plt.xlabel('Samples')
plt.show()
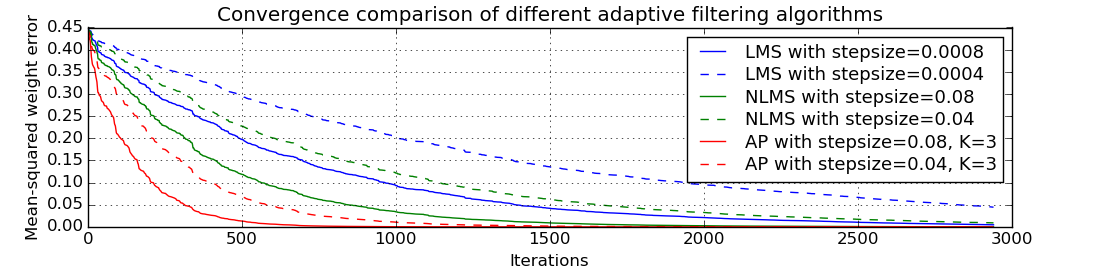
"""
Convergence comparison of different adaptive filtering algorithms (with
different step sizes) in white Gaussian noise.
"""
import numpy as np
import matplotlib.pyplot as plt
import adaptfilt as adf
# Generating input and desired signal
N = 3000
coeffs = np.concatenate(([-4, 3.2], np.zeros(20), [0.7], np.zeros(33), [-0.1]))
u = np.random.randn(N)
d = np.convolve(u, coeffs)
# Perform filtering
M = 60 # No. of taps to estimate
mu1 = 0.0008 # Step size 1 in LMS
mu2 = 0.0004 # Step size 1 in LMS
beta1 = 0.08 # Step size 2 in NLMS and AP
beta2 = 0.04 # Step size 2 in NLMS and AP
K = 3 # Projection order 1 in AP
# LMS
y_lms1, e_lms1, w_lms1 = adf.lms(u, d, M, mu1, returnCoeffs=True)
y_lms2, e_lms2, w_lms2 = adf.lms(u, d, M, mu2, returnCoeffs=True)
mswe_lms1 = adf.mswe(w_lms1, coeffs)
mswe_lms2 = adf.mswe(w_lms2, coeffs)
# NLMS
y_nlms1, e_nlms1, w_nlms1 = adf.nlms(u, d, M, beta1, returnCoeffs=True)
y_nlms2, e_nlms2, w_nlms2 = adf.nlms(u, d, M, beta2, returnCoeffs=True)
mswe_nlms1 = adf.mswe(w_nlms1, coeffs)
mswe_nlms2 = adf.mswe(w_nlms2, coeffs)
# AP
y_ap1, e_ap1, w_ap1 = adf.ap(u, d, M, beta1, K, returnCoeffs=True)
y_ap2, e_ap2, w_ap2 = adf.ap(u, d, M, beta2, K, returnCoeffs=True)
mswe_ap1 = adf.mswe(w_ap1, coeffs)
mswe_ap2 = adf.mswe(w_ap2, coeffs)
# Plot results
plt.figure()
plt.title('Convergence comparison of different adaptive filtering algorithms')
plt.plot(mswe_lms1, 'b', label='LMS with stepsize=%.4f' % mu1)
plt.plot(mswe_lms2, 'b--', label='LMS with stepsize=%.4f' % mu2)
plt.plot(mswe_nlms1, 'g', label='NLMS with stepsize=%.2f' % beta1)
plt.plot(mswe_nlms2, 'g--', label='NLMS with stepsize=%.2f' % beta2)
plt.plot(mswe_ap1, 'r', label='AP with stepsize=%.2f' % beta1)
plt.plot(mswe_ap2, 'r--', label='AP with stepsize=%.2f' % beta2)
plt.legend()
plt.grid()
plt.xlabel('Iterations')
plt.ylabel('Mean-squared weight error')
plt.show()