MasseyRamanujan

The Ramanujan Machine is an algorithmic approach to discover new mathematical conjectures. For the time being, the project is focused in number theory, specifically on finding formulas relating fundamental constants like pi, e, and the Riemann zeta function values to various continued fractions.

For more information, please go to RamanujanMachine.com.

Installation

Clone the repo and install the package. If you have pip, it can be done by running

pip install -e .

under the same folder as setup.py. That's it, you are now ready to discover new conjectures.

The MITM_RF algorithm:

The MITM algorithm will "mine" new Continued Fraction conjectures of the type: 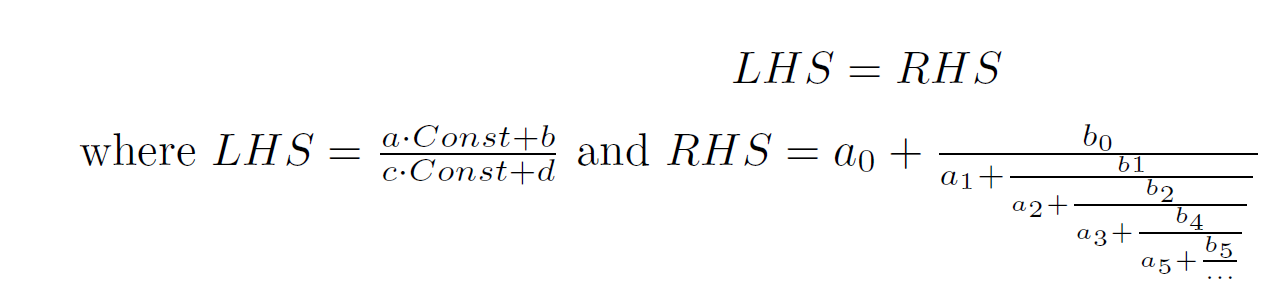This project lets you control the equation space scanned by the algorithm.

Running the code

To start a new execution, you'll need to configure three parts:

What LHS do you wish to scan
What structure does an and bn take, and what range do you wish to scan for each coefficient
How to decide if there was a match (precission wise)

you can see examples under scripts/ folder

Left Hand Side Hash Table (`LHSHashTable`)

This is a data structure that holds expressions made from the required constant. To create a LHS object, you'll need to choose a constant, and a range for all coefficients in the expression. The values generated are saved to a file to reduce execution time.

For example, the following code will generate all Mobius transforms of e, with coefficients between -5 and 5. The generated domain is saved to e_lhs_dept5

 from ramanujan.LHSHashTable import LHSHashTable
 from ramanujan.constants import g_const_dict

 saved_hash = 'e_lhs_dept5'
 lhs_coefs_range = 5
 lhs = LHSHashTable(
    saved_hash,
    lhs_coefs_range,
    [g_const_dict['e']])

`an` and `bn` Structures (any class under `poly_domains`)

An objects that generates pairs of an and bn series.

The simplest structure you can choose will be Xn = c0 * n^k + c1 * n^(k-1) + ... + ck for both an and bn (with the matching degree for each), when coefficient is independent of the rest.

This type of domain can be defined as follows:

 from ramanujan.poly_domains.CartesianProductPolyDomain import CartesianProductPolyDomain
 
 poly_search_domain = CartesianProductPolyDomain(
   2, [-5, 5], # an coefs
   2, [-5, 5]) # bn coefs

In this example, we've chosen both an and bn to be of degree 2, and the coefficients are integers that range from -5 to 5. All combination of coefficients under those restriction will be generated.

To create more intricate structures, you may create a class that extents CartesianProductPolyDomain or AbstractPolyDomains. You can take a look at ExampleDomain or Zeta3Domain1 as an example that expand this logic.

The Enumerator (any class under `enumerators`)

Last but not least, you'll need to choose an algorithm that compares the two.

The simplest, and fastest approach is implemented under EfficentGCFEnumerator. It follows a two-step process:

For any pair an and bn calculate the GCF to a dept of 30. Compare each result to values in LHSHashTable, using low precision and store matches.
The matches are re-evaluated to a dept of 1000, and compared again for higher precision, thus eliminating false positives. The final results are then presented as new conjectures.

For farther information regarding this algorithm, please refer to our paper 'the Ramanujan machine' under the 'MITM-RF algorithm' chapter, or visit our website RamanujanMachine.com.

For example, creating EfficientGCFEnumerator using the LHSHashTable and poly_domain defined above:

from ramanujan.enumerators.EfficientGCFEnumerator import EfficientGCFEnumerator

enumerator = EfficentGCFEnumerator(
    lhs,
    poly_search_domain,
    [g_const_dict['e']]
    )

And thats it! start your execution by running:

results = enumerator.full_execution()

Cool examples

Examples for conjectures can be found under scripts/paper_results. Just run every script there and start finding conjectures!

Tweaking the search parameters

Now that you've seen how to run the basic code, you can tweak the search parameters and find new conjectures of your own.

If you wish to change the searched series, you can create a new class that extends CartesianProductPolyDomain, and defines your new polynomial families. Please see poly_domains\ExampleDomain for a detailed example.

Jfaler/MasseyRamanujan