Modelling Simulation and Optimization: Optimization of a submarine hull
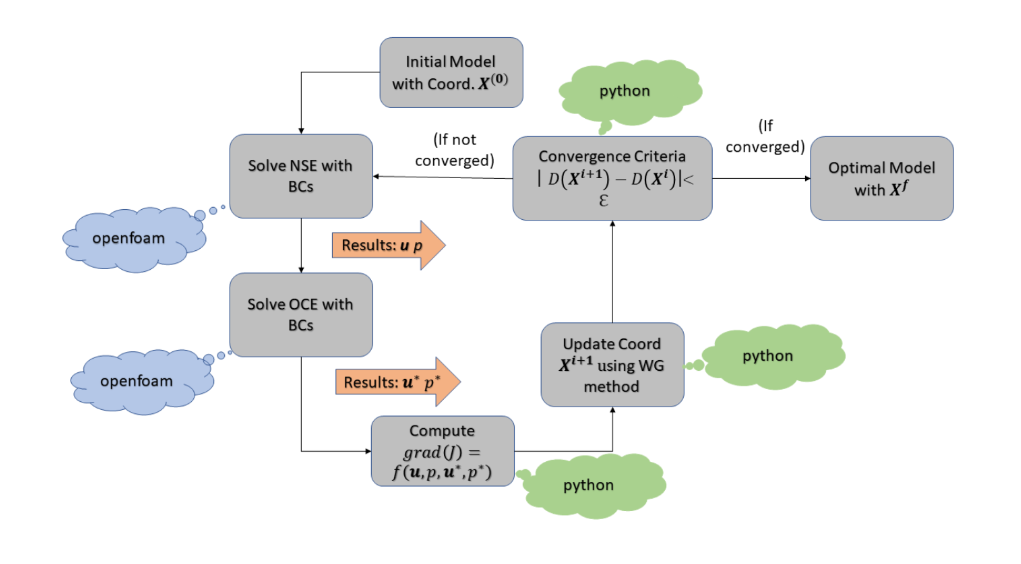
In this project, the optimization set up is implemented in a 2D spatial domain for a steady state, incompressible flow. The optimal state is defined by the reduction of drag force subjected to the body. An iterative procedure is followed to obtain a shape which experiences a lesser drag force compared to the previous iterations. The procedure is followed until a required tolerance for the drag force reduction is reached. An objective function representing the drag force is formulated mathematically and solved to obtain the optimality conditions. The objective function should be minimized satisfying the state equation and constant volume condition. An adjoint method is utilized to combine the constraints and the objective function. A weighted gradient method is used to update the coordinates.
First solve the NS equation(NS folder) to get the u and p, then use this to compute the variables in our objective function(OS folder).
openfoam6 is used for solving
-
compile the 'pisomosiFoam' solver
wclean wmake
-
define the case in 'Reference' folder(NS/system/blockMesh), if the shape needed to be changed
-
run the 'Runsimulation.py' code to run the simulation.
python3 Runsimulation.py
this runs the simulation and store the drag force value of each iteration in 'DragForce.dat'
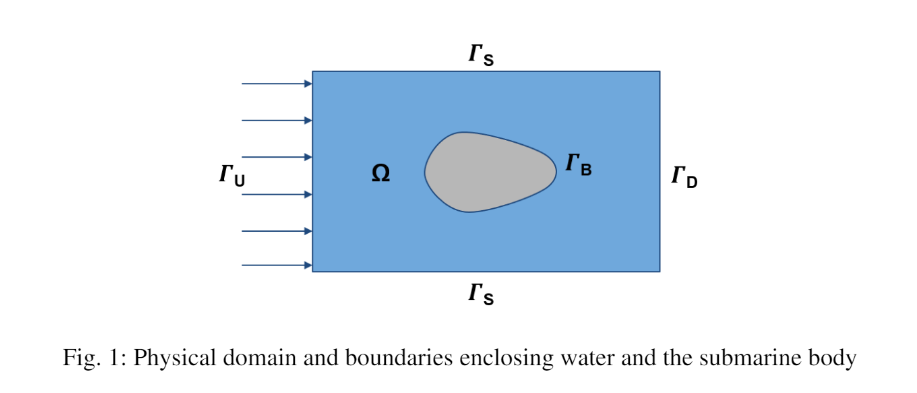
The domain used for simulatin is represented below.
The algorithm used for shape optimization is shown below
<p align="center">
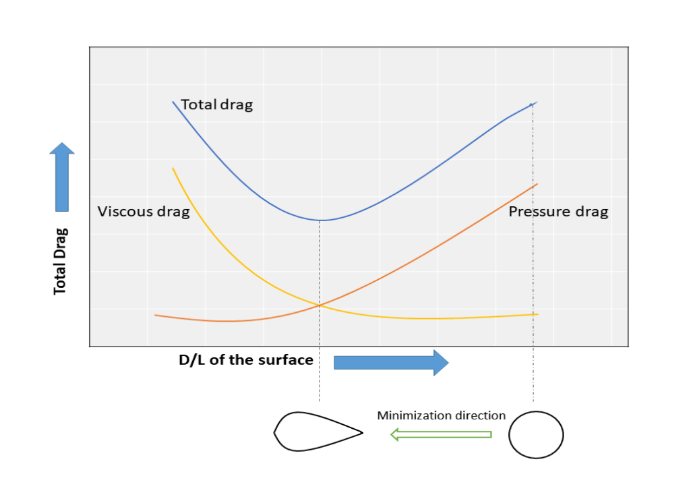
The direction of optimization in broader sense is shown as frictinal force components
<p align="center">
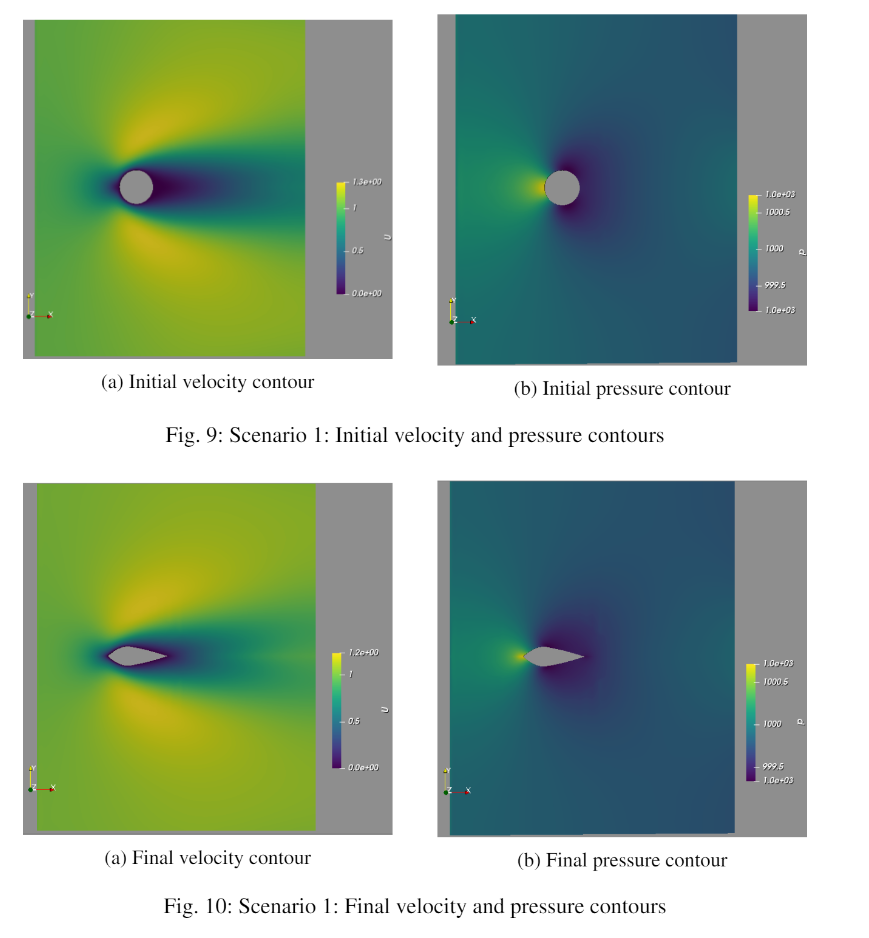
The final result for optimizing a spherical ball is shown below