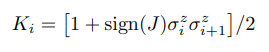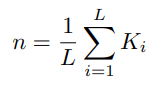A demonstration of using the fast-anneal protocol on a quantum computer to simulate the formation of topological defects in a 1D ring of spins undergoing a phase transition, as described by the Kibble-Zurek mechanism.
This example employs quantum annealing in the coherent regime of a D-Wave quantum processing unit (QPU), producing samples that align with the theoretical predictions.
The Kibble-Zurek mechanism relates, for a system driven through a phase transition, the formation of topological defects to the transition rate. This section provides an intuitive understanding of the mechanism.
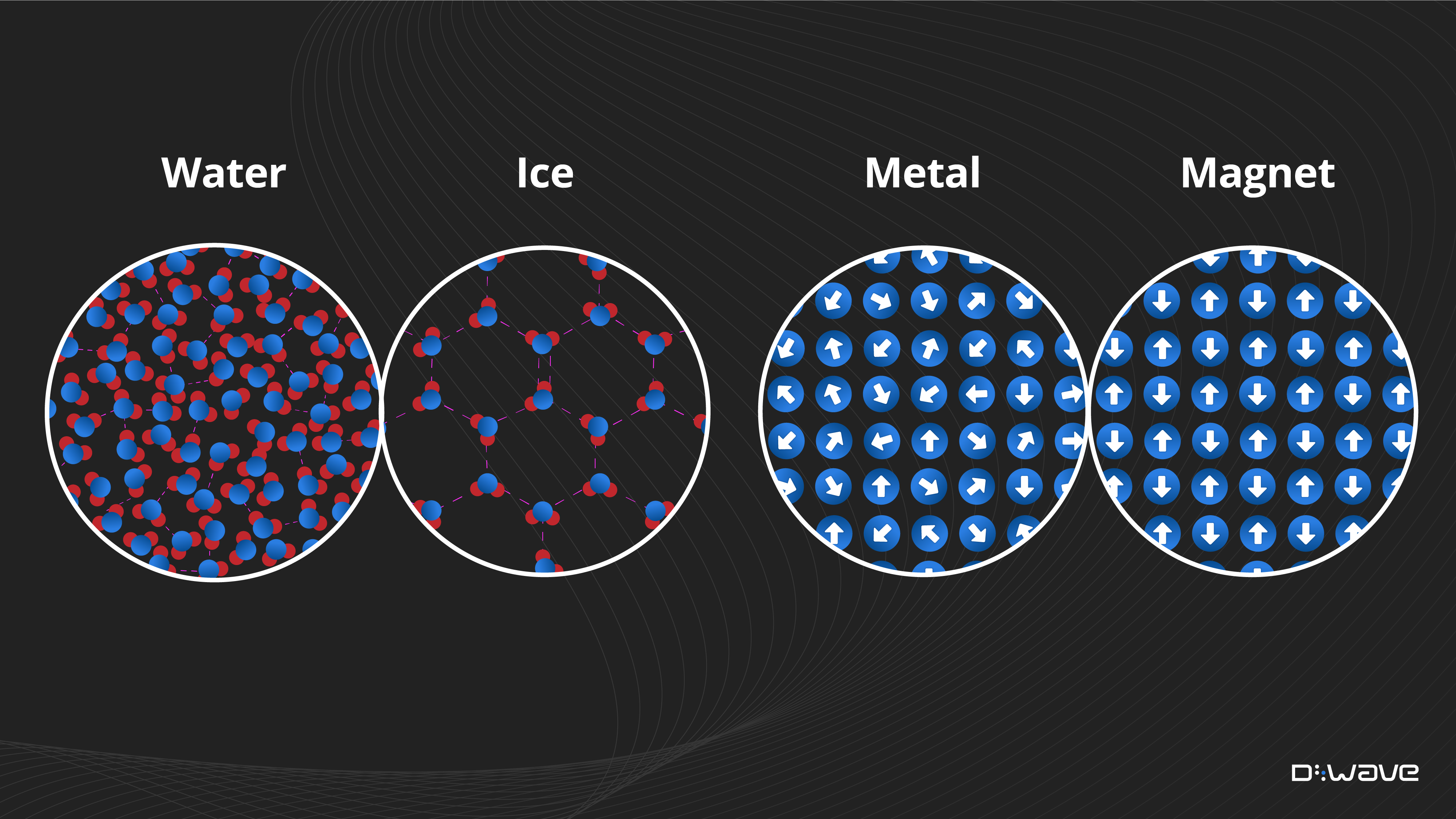
Some macroscopic phase transitions are familiar: a changing temperature will transition water (a liquid) to ice (a solid); it can also change the magnetic properties of metal.
In both cases, the material transitions between disorderly and orderly states:
- Orderly crystalline structure of ice versus the ongoing formation and breaking of hydrogen bonds in water.
- Aligned microscopic magnetic domains in a ferromagnet versus random orientations in a nonmagnetic metal.
Kibble's original formulation explained the transition of the hot post-Big Bang universe from highly symmetric to its current state, with its non-uniform distribution of galaxies etc.
Zurek expanded the idea to condensed matter and quantum phase transitions.
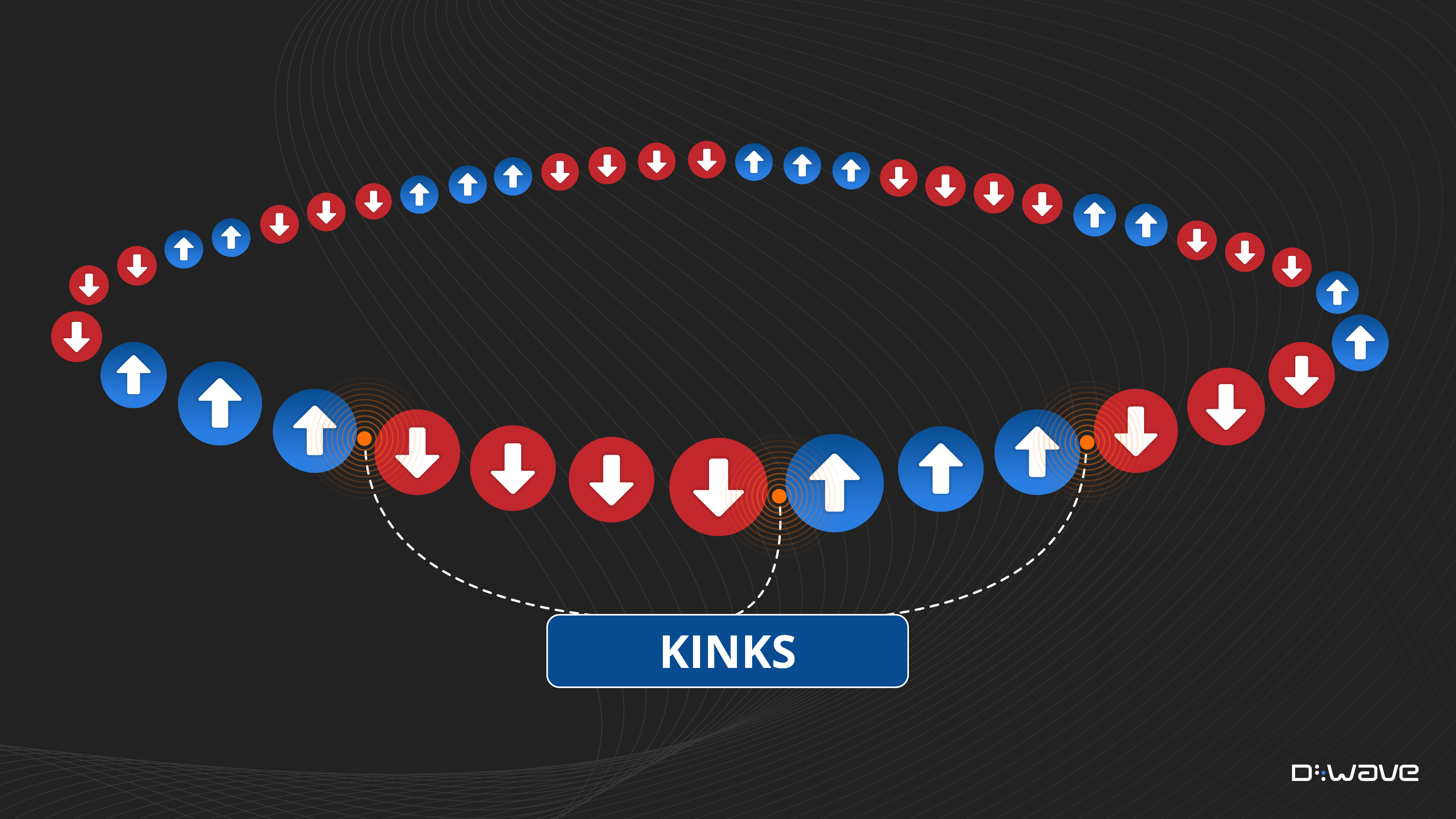
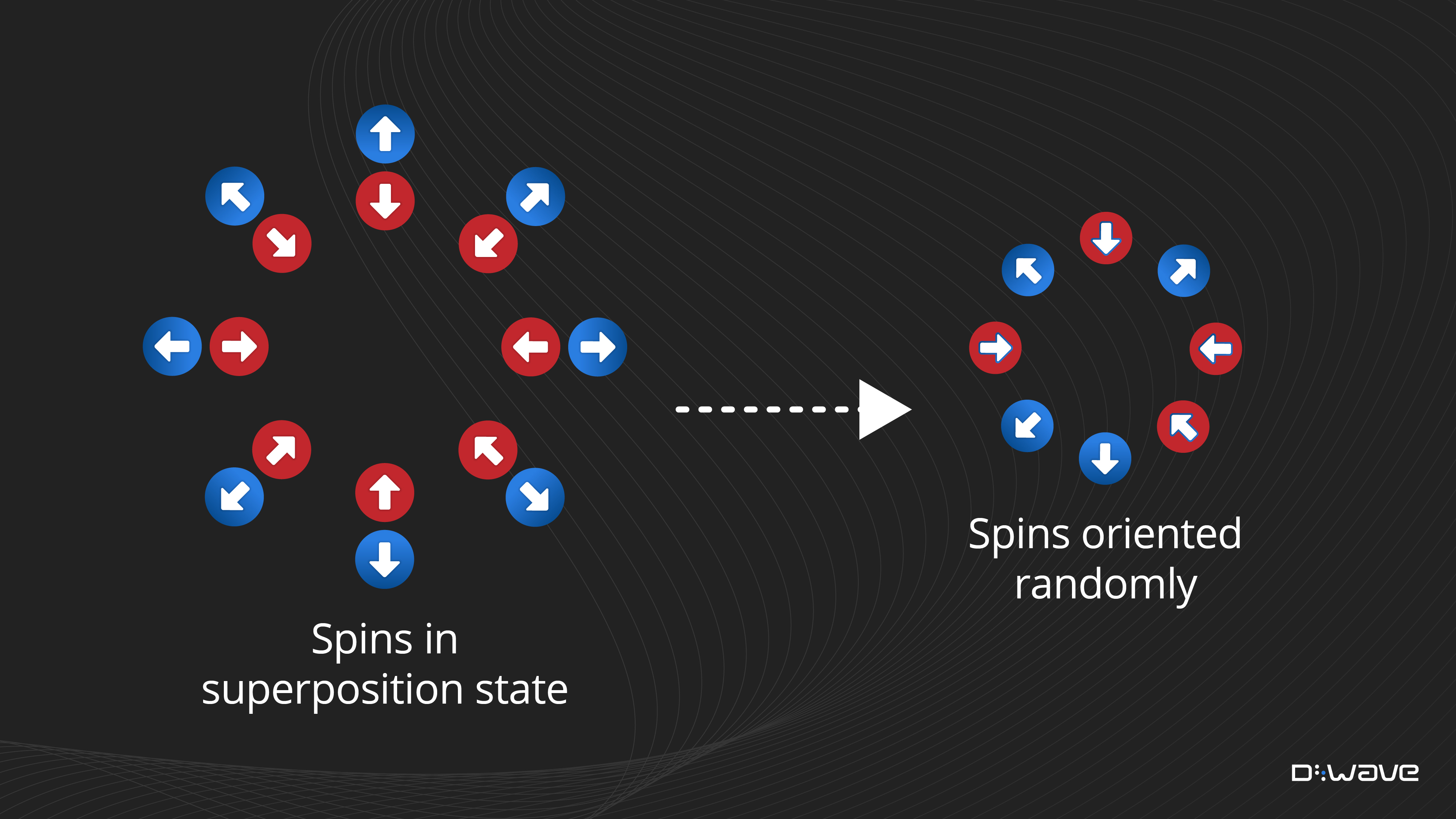
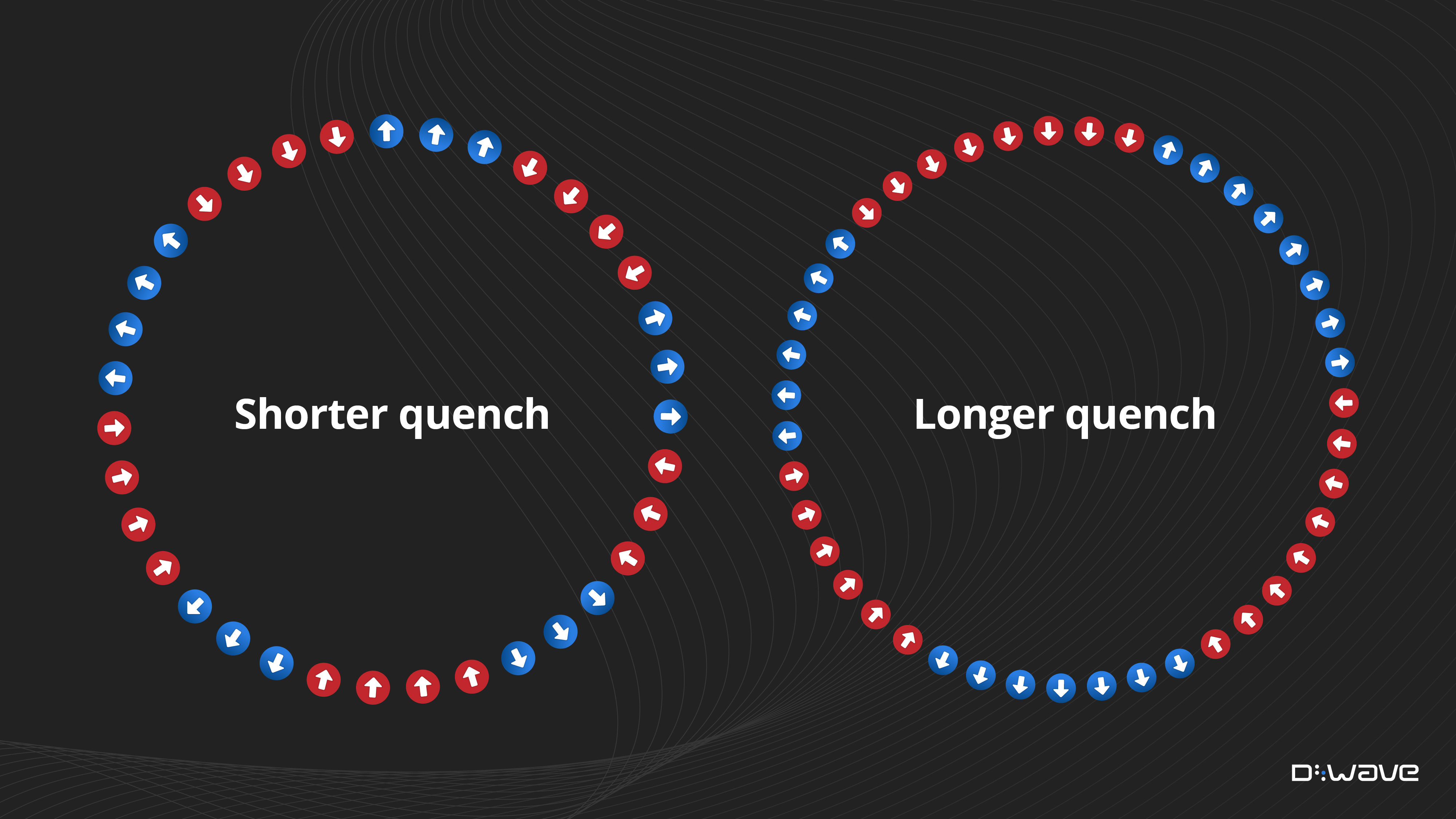
A quench is when a control parameter changes at a high rate compared to system dynamics; with D-Wave's fast-anneal protocol, the anneal schedule can be fast compared to thermalization times. For the simple system of a ring of ferromagnetically coupled spins, quenching (fast annealing) causes a transition from a state of spins in superposition to a state that has alternating segments of up/down spins. Switches from one segment to the next are called "kinks" (an example of topological defects).
For continuous or quantum phase transitions, the mechanism relates the density of defects (e.g. kinks) to the quench time as a universal scaling law.
Consider two extreme cases:
-
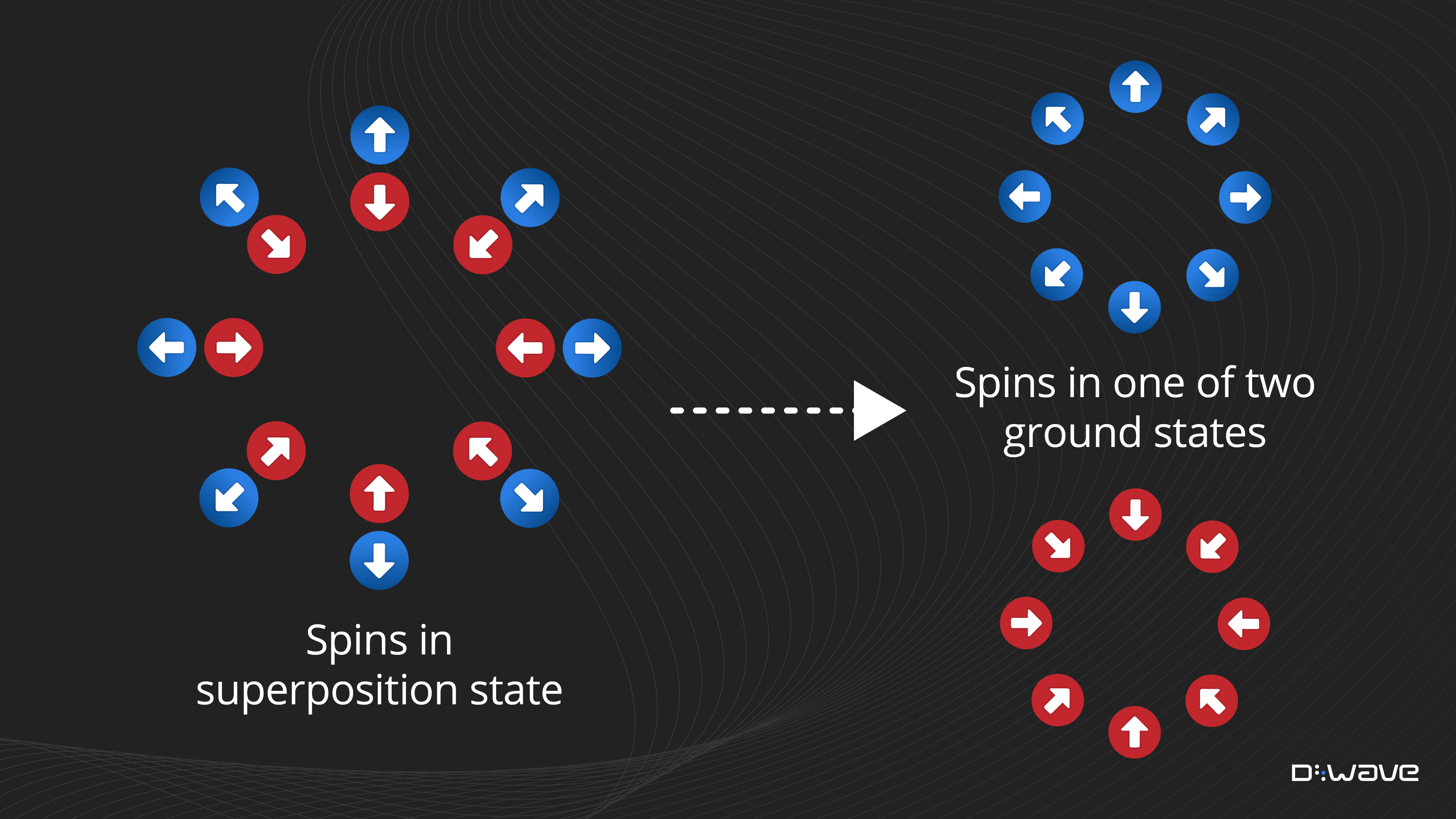
Ideal adiabatic transition.
At the end of a sufficiently slow anneal, the system ends in one of its two ground states: all spins up or all spins down.
-
Instantaneous quench.
Each spin independently orients up or down (in an unbiased system, both outcomes have equal probablility).
In between these two extremes, for fast quenches, the system ends in a state of alternating segments of up/down spins. The average length of these segments increases with the quench/anneal time. For this example of a quantum phase transition (a 1D ring of spins), the Kibble-Zurek mechanism predicts that the average length increases as a function of the square root of the anneal time.
You can run this example without installation in cloud-based IDEs that support the Development Containers specification (aka "devcontainers").
For development environments that do not support devcontainers, install
requirements:
pip install -r requirements.txt
If you are cloning the repo to your local system, working in a virtual environment is recommended.
Your development environment should be configured to access Leap’s Solvers. You can see information about supported IDEs and authorizing access to your Leap account here.
To run the demo:
python app.pyAccess the user interface with your browser at http://127.0.0.1:8050/.
The demo program opens an interface where you can configure problems, submit these problems to a quantum computer, and compare the results to the Kibble-Zurek predictions.
Hover over an input field to see a description of the input and its range of supported values.
Quantum simulation is valuable for demonstrating and understanding the capabilities of quantum computers. For example, the simulation of nonequilibrium dynamics of a magnetic spin system quenched through a quantum phase transition requires classical resources that grow exponentially with system size (see [2]). D-Wave's quantum computers can enable such research as described in [1], which studied coherent evolution through a quantum phase transition for a 1D transverse-field Ising chain. It observed, for long chains, the quantum Kibble-Zurek mechanism with theoretically predicted kink statistics; in small chains, excitation statistics validate the picture of a Landau-Zener transition at a minimum gap. In both cases, results were in quantitative agreement with analytical solutions to the closed-system quantum model.
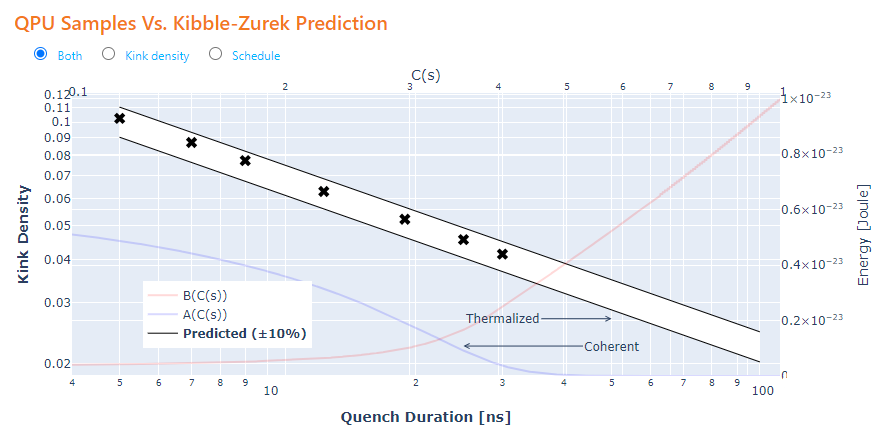
Comparing the theoretically predicted kink density against such a simulation on the quantum computer is done as follows.
To calculate kink density from samples returned from the quantum computer, define a kink operator,
where J is the coupling strength between qubits and
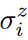 is the Pauli operator on the i-th
qubit. Put simply, for any sample returned from the quantum computer, the
operator gives 1 if there is a kink between qubits i and i+1 (i.e., if the
pair of qubits at the end of the anneal have different values for negative J
and identical values for positive J). If there is no kink between the pair,
the operator gives 0.
is the Pauli operator on the i-th
qubit. Put simply, for any sample returned from the quantum computer, the
operator gives 1 if there is a kink between qubits i and i+1 (i.e., if the
pair of qubits at the end of the anneal have different values for negative J
and identical values for positive J). If there is no kink between the pair,
the operator gives 0.
Define a kink-density operator as,
where L is the length of the chain of spins (the number of qubits coupled together).
Average kink density is obtained by sampling many times (the code in this
example sets num_reads=100) and averaging.
The research described in [1] performed a more sophisticated version of this experiment: it employed advanced calibration techniques not used here and also varied the temperature.
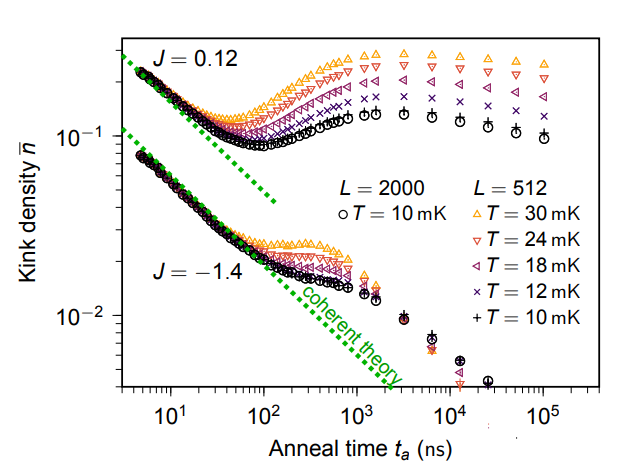
The plot below from the paper shows data for weak coupling, J=0.12, and strong coupling, J=−1.4, for a range of temperatures and anneal times. For strong coupling and fast anneals, the kink density is unaffected by temperature and agrees quantitatively with closed-system coherent quantum theory, shown as dotted green lines.
Note that as you increase the anneal time, you move from the coherent regime and the returned samples are increasingly affected by thermalization, pushing the kink density away from the predicted value.
Most the code related to configuring and analyzing the Ising problem is in the helpers/qa.py and helpers/kz_calcs.py files. The remaining files mostly support the user interface.
The helpers/qa.py file provides the following functions related to the use of the quantum computer:
-
create_bqm()generates a binary quadratic model (BQM) to represent the ring of spins with a given coupling strength. -
find_one_to_one_embedding()find a minor embedding for the problem with a single qubit representing each logical spin in the ring. The function makes a few attempts to find such an embedding. This function is used only if no valid cached minor-embedding is available for the quantum computer. -
Additional convenience functions.
The helpers/kz_calcs.py file provides the following functions related to Kibble-Zurek calculations:
-
theoretical_kink_density()calculates the kink density predicted for the configured coupling strength and annealing time. -
kink_stats()calculates the kink density for the sample set returned from the quantum computer.
You can find more information in the documentation and comments in those files.
Article [2] predicts a characteristic energy scale that is 20% smaller
than that of the
published annealing schedule
for quantum computer Advantage_system4.1 used by the Kibble-Zurek calculation
in the theoretical_kink_density() function. A comparable discrepancy between
the published and spectral-fit schedule is found in [1] (see section
"Extracting annealing schedules" in the supplementary material) for frustrated
rings of various length and energy scales. The code in the
theoretical_kink_density() function applies this correction of 0.80
to the published schedules.
Note: Standard practice for submitting problems to Leap solvers is to use a dwave-system sampler; for example, you typically use DWaveSampler for Ising problems. The code in this example uses the dwave-cloud-client, which enables finer control over communications with the Solver API (SAPI).
If you are learning to submit problems to Leap solvers, use a dwave-system
solver, with its higher level of abstraction and thus greater simplicity,
as demonstrated in most the code examples of the
example collection and in the
Ocean documentation.
[1] King, A.D., Suzuki, S., Raymond, J. et al. Coherent quantum annealing in a programmable 2,000 qubit Ising chain. Nat. Phys. 18, 1324–1328 (2022). https://doi.org/10.1038/s41567-022-01741-6
[2] King, A.D. et al. Computational supremacy in quantum simulation. https://arxiv.org/abs/2403.00910
Released under the Apache License 2.0. See LICENSE file.