Using Linear Programming to Solve Parametric Bernoulli Multi-Armed Bandit Problem

The starting point of this code was taken from https://github.com/gdmarmerola/interactive-intro-rl.

Running code

In main.py there should be everything to run the tests you could want.

Initialize bandit problem

You need to only change bandit_matrix and values in order to define a parametric bandit problem. The values represent the values for $\theta$ as you would expect. bandit_matrix is an np array of arrays. Each array represents one bandit, and its values the parameters of that banit. For instance:

bandit_matrix = np.array([[1, 0], [1, -1], [0, 1], [-0.4, 1.5]])
values = [0.6, 0.5]

represents

$$ \begin{equation} \begin{split} p_0 &= 1 \cdot \theta_0 + 0 \cdot \theta_1\\ p_1 &= 1 \cdot \theta_0 - 1 \cdot \theta_1\\ p_2 &= 0 \cdot \theta_0 + 1 \cdot \theta_1\\ p_3 &= -0.4 \cdot \theta_0 + 1.5 \cdot \theta_1\\ \theta &= \begin{pmatrix} 0.6 & 0.5 \end{pmatrix} \end{split} \end{equation} $$

Note that the length of each array in bandit_matrix should be equal to the length of bandit_probs, i.e. the dimension of the value space.

The other examples from the paper are

bandit_matrix = np.array(
    [
        [1.4, 0.2, -1, 0.6],
        [0.2, -0.5, 1.2, 0.2],
        [0.8, -0.1, 0, 1],
        [0.9, 0, 0, -0.5],
    ]
)
values = [0.3, 0.2, 0.3, 0.4]

for

$$ \begin{equation} \begin{split} p_0 &= 1.4 \cdot \theta_0 + 0.2 \cdot \theta_1 - 1 \cdot \theta_2 + 0.6 \cdot \theta_3 \\ p_1 &= 0.2 \cdot \theta_0 - 0.5 \cdot \theta_1 + 1.2 \cdot \theta_2 + 0.2 \cdot \theta_3 \\ p_2 &= 0.8 \cdot \theta_0 - 0.1 \cdot \theta_1 + 0 \cdot \theta_2 + 1 \cdot \theta_3 \\ p_3 &= 0.9 \cdot \theta_0 + 0 \cdot \theta_1 + 0 \cdot \theta_2 - 0.5 \cdot \theta_3\\ \theta &= \begin{pmatrix} 0.3 & 0.2 & 0.3 & 0.4 \end{pmatrix} \end{split} \end{equation} $$

bandit_matrix = np.array(
    [
        [1, 1, 1, 0, 0],
        [1, 1, 0, 1, 0],
        [1, 1, 0, 0, 1],
        [1, 0, 1, 1, 0],
        [1, 0, 1, 0, 1],
        [1, 0, 0, 1, 1],
        [0, 1, 1, 1, 0],
        [0, 1, 1, 0, 1],
        [0, 1, 0, 1, 1],
        [0, 0, 1, 1, 1],
    ]
)
values = [0.3, 0.3, 0.15, 0.1, 0.05]

for

$$ \begin{equation} \begin{split} p_0 &= 1 \cdot \theta_0 + 1 \cdot \theta_1 + 1 \cdot \theta_2 + 0 \cdot \theta_3 + 0 \cdot \theta_4 \\ p_1 &= 1 \cdot \theta_0 + 1 \cdot \theta_1 + 0 \cdot \theta_2 + 1 \cdot \theta_3 + 0 \cdot \theta_4 \\ p_2 &= 1 \cdot \theta_0 + 1 \cdot \theta_1 + 0 \cdot \theta_2 + 0 \cdot \theta_3 + 1 \cdot \theta_4 \\ p_3 &= 1 \cdot \theta_0 + 0 \cdot \theta_1 + 1 \cdot \theta_2 + 1 \cdot \theta_3 + 0 \cdot \theta_4 \\ p_4 &= 1 \cdot \theta_0 + 0 \cdot \theta_1 + 1 \cdot \theta_2 + 0 \cdot \theta_3 + 1 \cdot \theta_4 \\ p_5 &= 1 \cdot \theta_0 + 0 \cdot \theta_1 + 0 \cdot \theta_2 + 1 \cdot \theta_3 + 1 \cdot \theta_4 \\ p_6 &= 0 \cdot \theta_0 + 1 \cdot \theta_1 + 1 \cdot \theta_2 + 1 \cdot \theta_3 + 0 \cdot \theta_4 \\ p_7 &= 0 \cdot \theta_0 + 1 \cdot \theta_1 + 1 \cdot \theta_2 + 0 \cdot \theta_3 + 1 \cdot \theta_4 \\ p_8 &= 0 \cdot \theta_0 + 1 \cdot \theta_1 + 0 \cdot \theta_2 + 1 \cdot \theta_3 + 1 \cdot \theta_4 \\ p_9 &= 0 \cdot \theta_0 + 0 \cdot \theta_1 + 1 \cdot \theta_2 + 1 \cdot \theta_3 + 1 \cdot \theta_4 \\ \theta &= \begin{pmatrix} 0.3 & 0.3 & 0.15 & 0.1 & 0.05 \end{pmatrix} \end{split} \end{equation} $$

Plot

With plot.plot_MAB_experiment you can plot one run of a mab experiment as a video or frame like this:

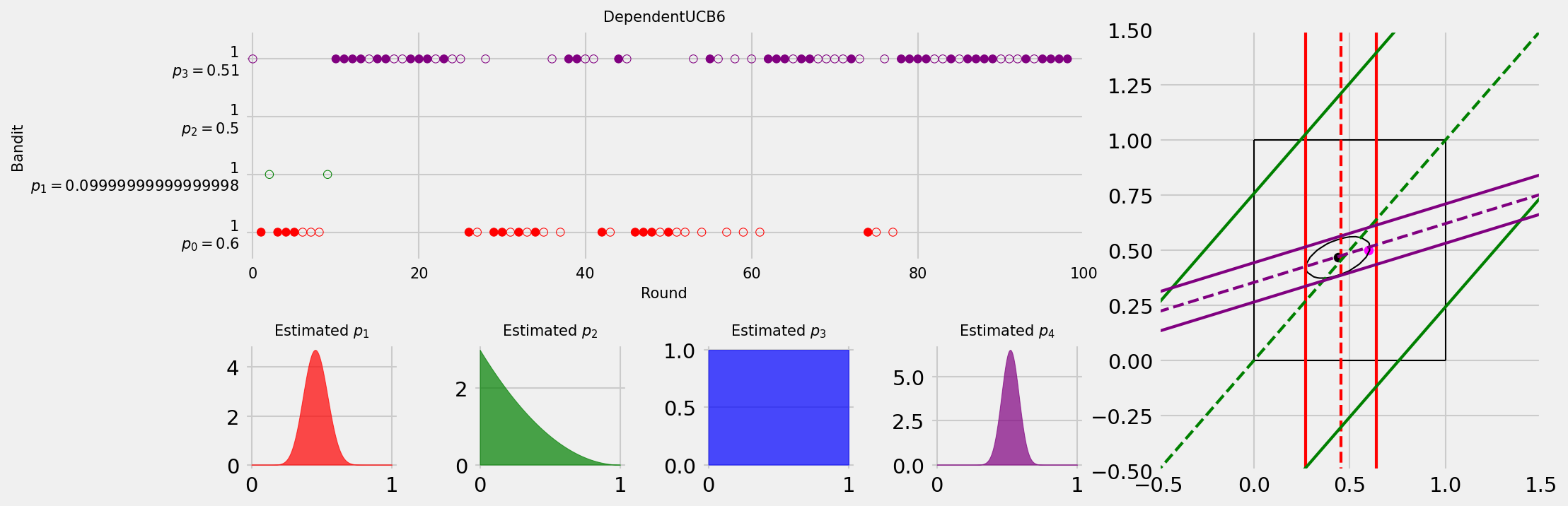
def plot_MAB_experiment(
    decision_policy,
    mab,
    N_DRAWS,
    bandit_probs,
    plot_title,
    graph=True,
    video=False,
    column_vecs=None,
    theta_values=None,
    alpha=None,
)

Arguments:

decision_policy(k_array, reward_array, n_bandits) where k_array is a list of bandits where each bandit is a list of zeroes and ones whether that bandit was picked that round in the history, and reward_array is the same but the reward for that bandit in each round, and n_bandits is the number of bandits. It should return what bandit to play.
mab the multi-armed bandit problem like class MAB in main.py.
N_DRAWS the number of draws
plot_title title
graph whether to show the graph shown on the right side of the image.
video whether to show a video where each round is a frame, or just output the last frame.
column_vecs column vectors as for LinUCB in order to make the ellipsoid work for the graph
theta_values the actual value for $\theta$ to be used for the graph.
alpha the $\alpha$ for the ellipsoid from LinUCB in the graph.

Simulation

Simulates some number of runs of multiple policies on a certain MAB. This can then be input into plot_simulation to plot this:

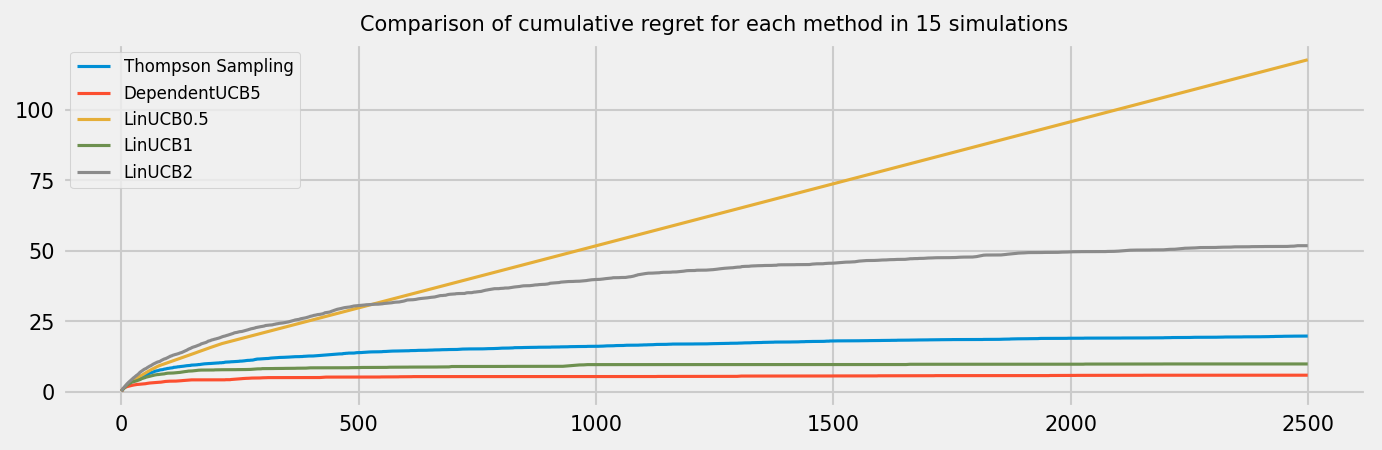
def simulation(
    mab,
    policies,
    n_rounds=1000,
    n_simulations=1000,
    uncertainty=None,
):

Returns a dictionary which has for every policy:

k_array for every bandit for every round number of times that bandit was selected that round
reward_array for every bandit for every round number of times that bandit gave a reward in that round
regret_array for every simulation for every round the regret

def plot_simulation(
    results_dict,
    n_bandits,
    plot_reward=False
):

Arguments

mab the multi-armed bandit problem like class MAB in main.py.
policies a dictionary of policies to run on the bandit problem.
n_rounds the number of rounds
n_simulations the number of simulations with each n_rounds rounds.
plot_reward whether to plot the cumulative reward as well as the cumulative regret.
uncertainty if this is given it adds some uncertainty 'noise'. It adds to each bandit probability a certain error which is drawn from a uniform distribution between -uncertainty and +uncertainty. These errors are added at the start and then all policies are run on the same probabilities for all simulations.

Policies