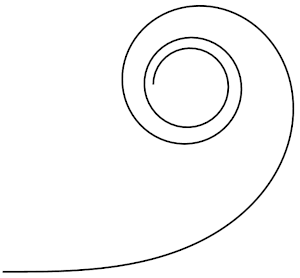
Fresnel integrals are two functions C(t) and S(t) that evaluate to the x and y coordinates of the Eurler spiral a.k.a. a clothoid (see https://en.wikipedia.org/wiki/Fresnel_integral), which has some interesting properties:
- The length of the spiral from 0 to t is... t.
- The tangent to the spiral at position t is at the angle... t2 (in radians).
- The curvature κ at t is... 2t.
The spiral starts at (0, 0) and converges around and onto x = y = (1/2)*sqrt(pi/2).
This package contains a Javascript port of an algorithm implemented by W. V. Snyder of the Jet Propulsion Laboratory in January 1992. The original code is in Fortran and was downloaded from http://www.netlib.org/toms/ in July 2020.
The original code was marked as follows:
ALGORITHM 723, COLLECTED ALGORITHMS FROM ACM.
THIS WORK PUBLISHED IN TRANSACTIONS ON MATHEMATICAL SOFTWARE,
VOL. 22, NO. 4, December, 1996, P. 498--500.
Originally appeared in
VOL. 19, NO. 4, December, 1993, P. 452--456
Copyright (C) 1992, California Institute of Technology.
U. S. Government sponsorship under NASA contract NAS7-918 is acknowledged.
Some parts were additionally marked as originally from the Naval Surface Warfare Center, a U.S. government agency. And the source code was published by the ACM, which may also claim copyright.
Although the original code indicates it is copyrighted, I have posted this port without any particular license to do so. Evaluate your own risk when using this package. To the extent that I have any copyright claims to this port, I waive them.
Another solution of the Fresnel integrals can be found at http://www.netlib.org/cephes/qlibdoc.html#qfresnl.
To evaluate the Fresnel integrals at t, call:
const Fresnel = require("./index.js");
var point = Fresnel(t);
console.log(point.x, point.y);The Fresnel function returns an object with properties x and y, which correspond to the Fresnel functions C(t) and S(t), respectively. The object additionally as properties f and g which are related functions also solved by the original library.
For example:
const Fresnel = require("./index.js");
const L = 200;
console.log('<svg viewBox="0 0 200 200" xmlns="http://www.w3.org/2000/svg">');
console.log('<polyline fill="none" stroke="black" points="');
for (let i = 0; i < 200; i++) {
var pt = Fresnel(i / 60);
console.log(pt.x*L + "," + pt.y*L)
}
console.log('"/>');
console.log('</svg>')