NOTE: this package is now at sfdep
This package is superceded by sfdep.
Please download and use sfdep.
NOTE: this package is under active and experimental development. Functions are likely to change.
sfweight is an opinionated translation of the wonderful spdep package. The goal is to provide a streamlined method of doing spatial statistics that works with sf objects, data frames, and the tidyverse. spdep is more flexible with the types of input objects and a bit more idiosyncratic in the syntax that is used.
You can install the development version from GitHub with
remotes::install_github("Josiahparry/sfweight")We can fit a spatial Durbin model by calculating spatially lagged predictors.
library(sfweight)
library(tidyverse)
acs_lagged <- acs %>%
mutate(nb = st_contiguity(geometry),
wts = st_weights(nb),
trans_lag = st_lag(by_pub_trans, nb, wts),
bach_lag = st_lag(bach, nb, wts))
durbin_lm <- lm(med_house_income ~ trans_lag + by_pub_trans + bach_lag + bach,
data = acs_lagged)
broom::tidy(durbin_lm)
#> # A tibble: 5 × 5
#> term estimate std.error statistic p.value
#> <chr> <dbl> <dbl> <dbl> <dbl>
#> 1 (Intercept) 56187. 9812. 5.73 3.76e- 8
#> 2 trans_lag -13479. 28078. -0.480 6.32e- 1
#> 3 by_pub_trans -43067. 18841. -2.29 2.33e- 2
#> 4 bach_lag -40154. 28287. -1.42 1.57e- 1
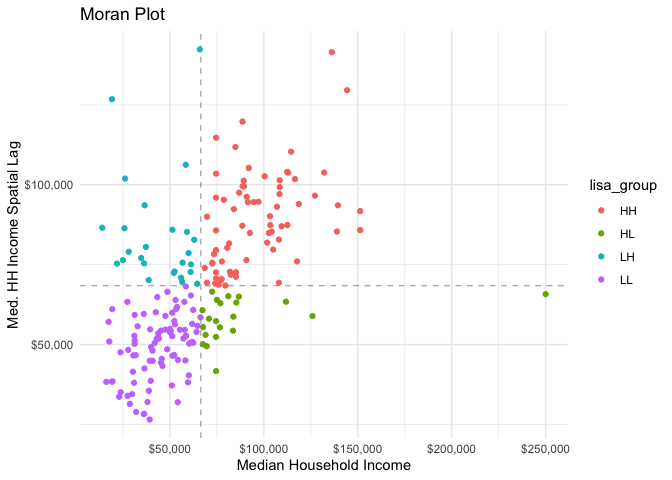
#> 5 bach 153955. 21490. 7.16 1.51e-11We can create a Moran plot by creating a spatially lagged variable.
Additionally the function categorize_lisa() will categorize high-high,
high-low, etc., groupings of these variables.
acs_lagged %>%
mutate(inc_lag = st_lag(med_house_income, nb, wts),
lisa_group = categorize_lisa(med_house_income, inc_lag)) %>%
ggplot(aes(med_house_income, inc_lag, color = lisa_group)) +
geom_vline(aes(xintercept = mean(med_house_income)), lty = 2, alpha = 1/3) +
geom_hline(aes(yintercept = mean(inc_lag)), lty = 2, alpha = 1/3) +
geom_point() +
labs(title = "Moran Plot",
y = "Med. HH Income Spatial Lag",
x = "Median Household Income") +
theme_minimal() +
scale_x_continuous(labels = scales::dollar) +
scale_y_continuous(labels = scales::dollar)We can also calculate the Local Moran’s I for each observation using the
function local_moran() this will create a dataframe column containing
the I, expected I, variance, Z-value, and P-value for each observation.
You can extract this using tidyr::unnest().
acs %>%
mutate(nb = st_contiguity(geometry),
wt = st_weights(nb),
lisa = local_moran(med_house_income, nb, wt)) %>%
unnest(lisa) %>%
ggplot(aes(fill = lisa_category)) +
geom_sf(color = "black", lwd = 0.25) +
scale_fill_manual(values = c("HH" = "#528672","LL" = "#525586", "Insignificant" = NA))str(acs)
#> sf [203 × 5] (S3: sf/tbl_df/tbl/data.frame)
#> $ fips : chr [1:203] "25025092101" "25025100603" "25025010103" "25025070402" ...
#> $ med_house_income: num [1:203] 52924 86659 31218 25750 68500 ...
#> $ by_pub_trans : num [1:203] 0.3208 0.0945 0.1815 0.2229 0.199 ...
#> $ bach : num [1:203] 0.124 0.305 0.405 0.141 0.208 ...
#> $ geometry :sfc_MULTIPOLYGON of length 203; first list element: List of 1
#> ..$ :List of 1
#> .. ..$ : num [1:136, 1:2] -71.1 -71.1 -71.1 -71.1 -71.1 ...
#> ..- attr(*, "class")= chr [1:3] "XY" "MULTIPOLYGON" "sfg"
#> - attr(*, "sf_column")= chr "geometry"
#> - attr(*, "agr")= Factor w/ 3 levels "constant","aggregate",..: NA NA NA NA
#> ..- attr(*, "names")= chr [1:4] "fips" "med_house_income" "by_pub_trans" "bach"We can get neighbors based on Queen contiguities with st_contiguity().
nbs <- st_contiguity(acs)
nbs[1:5]
#> [[1]]
#> [1] 2 15 168 171 172 179 180
#>
#> [[2]]
#> [1] 1 71 180
#>
#> [[3]]
#> [1] 45 50 92 122
#>
#> [[4]]
#> [1] 30 84 127 135 136 138
#>
#> [[5]]
#> [1] 34 87 100 108If needed, we can also identify the cardinalities from the neighbors list as well.
st_cardinalties(nbs)
#> [1] 7 3 4 6 4 4 7 5 2 4 8 5 6 1 9 5 4 6 5 8 8 3 5 7 4
#> [26] 5 3 4 4 4 4 6 4 5 6 5 8 7 5 2 8 6 5 10 5 4 5 3 5 4
#> [51] 3 9 4 7 6 7 4 6 7 7 4 10 5 6 5 5 4 4 9 4 3 4 3 4 3
#> [76] 5 2 8 8 11 7 8 8 5 5 5 5 9 6 5 7 11 10 3 6 6 3 5 2 6
#> [101] 6 7 5 4 6 4 5 9 4 9 4 5 7 4 6 3 5 5 4 4 6 6 6 6 5
#> [126] 7 8 4 4 5 7 3 6 4 11 7 3 7 5 9 6 4 4 5 7 5 6 5 5 6
#> [151] 7 9 4 7 8 7 6 6 6 7 6 5 8 4 6 6 7 6 8 7 7 4 7 6 9
#> [176] 5 7 4 9 5 8 4 5 5 6 6 5 5 6 3 5 6 6 6 5 3 5 6 6 6
#> [201] 3 5 6We can get the weights from the neighbor contiguities as well. By
default, st_weights() uses row standardization.
wts <- st_weights(nbs)
wts[1:5]
#> [[1]]
#> [1] 0.1428571 0.1428571 0.1428571 0.1428571 0.1428571 0.1428571 0.1428571
#>
#> [[2]]
#> [1] 0.3333333 0.3333333 0.3333333
#>
#> [[3]]
#> [1] 0.25 0.25 0.25 0.25
#>
#> [[4]]
#> [1] 0.1666667 0.1666667 0.1666667 0.1666667 0.1666667 0.1666667
#>
#> [[5]]
#> [1] 0.25 0.25 0.25 0.25We can also calculate the spatial lag with the weights and neighbors.
inc_lag <- st_lag(acs$med_house_income, nbs, wts)
inc_lag[1:5]
#> [1] 63968.57 65019.00 59271.38 86385.17 73962.88If we have point data we can also identify the k-nearest neighbors with
st_knn(). For an example we can use the airbnb dataset that’s
imported with sfweight.
airbnb
#> Simple feature collection with 3799 features and 4 fields
#> Geometry type: POINT
#> Dimension: XY
#> Bounding box: xmin: -71.1728 ymin: 42.23576 xmax: -70.99595 ymax: 42.39549
#> Geodetic CRS: WGS 84
#> # A tibble: 3,799 × 5
#> id neighborhood room_type price geometry
#> * <dbl> <chr> <chr> <dbl> <POINT [°]>
#> 1 3781 East Boston Entire home/apt 125 (-71.02991 42.36413)
#> 2 5506 Roxbury Entire home/apt 145 (-71.09559 42.32981)
#> 3 6695 Roxbury Entire home/apt 169 (-71.09351 42.32994)
#> 4 8789 Downtown Entire home/apt 99 (-71.06265 42.35919)
#> 5 10730 Downtown Entire home/apt 150 (-71.06185 42.3584)
#> 6 10813 Back Bay Entire home/apt 179 (-71.08904 42.34961)
#> 7 10986 North End Entire home/apt 125 (-71.05075 42.36352)
#> 8 16384 Beacon Hill Private room 50 (-71.07132 42.3581)
#> 9 18711 Dorchester Entire home/apt 154 (-71.06096 42.32212)
#> 10 22195 Back Bay Private room 115 (-71.0793 42.34558)
#> # … with 3,789 more rowsairbnb_knn <- st_knn(airbnb)
airbnb_knn[1:5]
#> [[1]]
#> [1] 3091
#>
#> [[2]]
#> [1] 21
#>
#> [[3]]
#> [1] 2886
#>
#> [[4]]
#> [1] 1068
#>
#> [[5]]
#> [1] 203Point based weights implemented based on Luc Anselin and Grant Morrison’s notes.
Inverse distance band
airbnb_idw <- st_inverse_weights(airbnb$geometry, airbnb_knn)
airbnb_idw[1]
#> [[1]]
#> [1] 72.85418 94.82628 80.81517 76.98118 77.47322 207.58305 90.54686
#> [8] 140.95536 89.09559 130.49453 168.12971 76.88485 132.13504 169.34664
#> [15] 123.56357 110.04713 462.67599 73.68500 491.86866 88.92867 91.93710
#> [22] 391.89760 73.37702 81.09685 107.10884 139.86709 80.59692 111.15096
#> [29] 113.25885 126.51082 113.95462 107.27650 107.80669 108.08046 106.77599
#> [36] 98.56036 96.98179 105.01340 93.91173 91.75525 98.75033 94.91645
#> [43] 106.71431 86.72350 104.85322 80.03740 85.86828 78.68751 91.18164
#> [50] 80.82558 91.50620 87.66654 91.08201 78.62795 109.01413 94.83290
#> [57] 144.36684 133.21065 159.53591 121.62878 103.27084 108.61908 223.55088
#> [64] 132.34225 93.48938 98.53665 195.96026 272.30270 95.61728 150.25611
#> [71] 919.21712 113.75560 143.05836 135.91442 139.71490 106.91507 124.54847
#> [78] 153.71365 153.71365 153.71365 148.79092 74.75811Available kernels are:
- uniform
- triangular
- epanechnikov
- quartic
- gaussian
airbnb_gauss <- st_kernel_weight(airbnb$geometry, airbnb_knn, "gaussian")
airbnb_gauss[1]
#> [[1]]
#> [1] 2.506628 1.520893 1.866407 1.670106 1.602290 1.611395 2.357012 1.813899
#> [9] 2.193421 1.794732 2.145140 2.282160 1.600493 2.153400 2.285228 2.106956
#> [17] 2.013664 2.475767 1.538029 2.479302 1.792480 1.831595 2.463717 1.531722
#> [25] 1.674815 1.989288 2.188852 1.666432 2.022398 2.038470 2.123876 2.043607
#> [33] 1.990725 1.995231 1.997536 1.986418 1.907777 1.890761 1.970839 1.855665
#> [41] 1.829317 1.909780 1.867452 1.985884 1.761789 1.969390 1.656914 1.749397
#> [49] 1.633347 1.822058 1.670281 1.826179 1.775132 1.820787 1.632287 2.005285
#> [57] 1.866483 2.207137 2.158667 2.258595 2.095253 1.954776 2.002027 2.377080
#> [65] 2.154424 1.850619 1.907527 2.339361 2.418562 1.875498 2.228826 2.498773
#> [73] 2.042146 2.201982 2.171412 2.188205 1.987620 2.112729 2.240502 2.240502
#> [81] 2.240502 2.223651 1.559591acs %>%
transmute(nb = st_contiguity(geometry),
nb_2 = st_nb_lag(nb, 2),
nb_cumul_2 = st_nb_lag_cumul(nb, 2))
#> Simple feature collection with 203 features and 3 fields
#> Geometry type: MULTIPOLYGON
#> Dimension: XY
#> Bounding box: xmin: -71.19125 ymin: 42.22793 xmax: -70.9201 ymax: 42.45012
#> Geodetic CRS: WGS 84
#> # A tibble: 203 × 4
#> nb nb_2 nb_cumul_2 geometry
#> * <list> <list> <list> <MULTIPOLYGON [°]>
#> 1 <int [7]> <int [17]> <int [24]> (((-71.06249 42.29221, -71.06234 42.29273, -…
#> 2 <int [3]> <int [6]> <int [9]> (((-71.05147 42.28931, -71.05136 42.28933, -…
#> 3 <int [4]> <int [13]> <int [17]> (((-71.11093 42.35047, -71.11093 42.3505, -7…
#> 4 <int [6]> <int [18]> <int [24]> (((-71.06944 42.346, -71.0691 42.34661, -71.…
#> 5 <int [4]> <int [9]> <int [13]> (((-71.13397 42.25431, -71.13353 42.25476, -…
#> 6 <int [4]> <int [12]> <int [16]> (((-71.04707 42.3397, -71.04628 42.34037, -7…
#> 7 <int [7]> <int [13]> <int [20]> (((-71.01324 42.38301, -71.01231 42.38371, -…
#> 8 <int [5]> <int [8]> <int [13]> (((-71.00113 42.3871, -71.001 42.38722, -71.…
#> 9 <int [2]> <int [14]> <int [16]> (((-71.05079 42.32083, -71.0506 42.32076, -7…
#> 10 <int [4]> <int [11]> <int [15]> (((-71.11952 42.28648, -71.11949 42.2878, -7…
#> # … with 193 more rows